数组的排序算法
选择排序
每次选择所要排序得数组中的最大值(由大到小排序,由小到大排序则选择最小值)的数组元素,将这个数组元组的值与最前面没有排序的数组元素进行交换,
第一次排序之后,最大的数字来到了第一位,再从第二个元素开始找,找到最大的元素,与第二个交换位置
#include <stdio.h>
int main(int argc, char *argv[])
{
int i,j;
int a[10];
int temp;
int index;
printf("为数组元素赋值\n");
for(i=0;i<10;i++){
printf("a[%d]=",i);
scanf("%d",&a[i]);
}
for(i=0;i<9;i++){//外层循环0~8这9个元素
temp=a[i]; //假设最大值
index=i; // 记录假设最大值索引
for(j=i+1;j<10;j++){// 内层循环,排序后的元素
if(a[j]>temp){//取最大值
temp=a[j]; //重置最大值
index=j; //重置最大值索引
}
}
// 交换元素位置
a[index]=a[i];
a[i]=temp;
}
// 输出数组
for(i=0;i<10;i++){
printf("%d\t",a[i]);
if(i==4){ //输出换行
printf("\n");
}
}
return 0;
}
python做选择排序
# 扫描无序区,从无序区中找出一个极端值,放入有序区
def select_sort(li): # 选择
for i in range(len(li)-1): # i表示第几次,有多少元素我就要扫几-1次
# 找无序区最小值,保存最小值的位置
min_pos = i # 假设起始值最小,min_pos保存最小值的索引
for j in range(i+1, len(li)): # 第i趟开始时 无序区:li[i:],自己不与自己比较,所以i+1
if li[j] < li[min_pos]: # 满足条件,我存的值比后面的值大,则把后面的值的所以设置为最小值索引
min_pos = j
li[min_pos], li[i] = li[i], li[min_pos] # 交换两个值的位置
冒泡排序
每次比较相邻的两个数,将最小的数(从小到大排序)排在较大的数前面.
经过一次排序之后最小的数到达了最前面的位置,并将其他的数字依次向后移动,第二次排序时,将从第二个数开始最小的数移动到第二的位置,依次类推
#include <stdio.h>
int main(int argc, char *argv[])
{
int i,j;
int a[10];
int temp;
printf("为数组元素赋值\n");
for(i=0;i<10;i++){
printf("a[%d]=",i);
scanf("%d",&a[i]);
}
for(i=1;i<10;i++){//外层循环1~9这9个元素
for(j=9;j>=i;j--){//从后向前循环i后面的元素
if(a[j]<a[j-1]){//前面的数大于后面的数,交换
temp=a[j-1];
a[j-1]=a[j];
a[j]=temp;
}
}
}
// 输出数组
for(i=0;i<10;i++){
printf("%d\t",a[i]);
if(i==4){ //输出换行
printf("\n");
}
}
return 0;
}
python做冒泡排序
# 冒泡排序,一遍遍扫描未归位区,比较相邻的两个数字,满足条件则交换,每次使一个元素归位
def bubble_sort(li): # 冒泡
for i in range(len(li)-1): # i表示第几次,有多少元素我就要扫几-1次
for j in range(len(li)-i-1): # 比较元素的位置,len(li)-1-i是未归位区的最大索引
if li[j] > li[j+1]: # 满足条件 将两个数值交换,这里是前面比后面大
li[j], li[j+1] = li[j+1], li[j]
def bubble_sort_1(li): # 优化冒泡
for i in range(len(li)-1): # i表示第几次,有多少元素我就要扫几次
exchange = False # 增加了一个标志位,如果依次循环中没有发生交换,则顺序已经是有序的了,可以直接退出
for j in range(len(li)-i-1): # 比较元素的位置,len(li)-1-i是未归位区的最大索引
if li[j] > li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
exchange = True
if not exchange:
return
插入排序
插入排序就像是摸扑克,第一张算是有序区,从后面的无序区拿扑克向有序区中插
python
def insert_sort(li): # 插入
for i in range(1, len(li)): # i是摸到的牌的下标,第一个属于有序区,所以从第二个开始
tmp = li[i] # 手里牌的大小
j = i - 1 # j是手里最后一张牌的下标
# 如果tmp大于我手里第j个元素,他就应该放在第j个位置上,如果小于就继续向前比较
while j >= 0 and li[j] > tmp: # 两个终止条件:j小于0表示tmp是最小的 顺序不要乱
# 因为保存了i索引位置的值,所以大于tmp的数都向后移动一位,j自减
li[j+1] = li[j]
j -= 1
li[j+1] = tmp
快速排序
快排采用的递归的思路
是以一个数字为基准(第0个元素),将列表分为大于他的和小于他的两部分,递归进行直至列表少于一个元素
但是当使用快排排列反向元素时,所用的时间会哒哒哒增加,因为始终有一部分是空的,而另一部分是满的
def partition(li, left, right): # 归位
# randi = random.randint(left, right)
# li[randi], li[left] = li[left], li[randi]
'''
将一个列表分成左右两部分
:param li: 列表
:param left: 开始索引
:param right: 结束索引
:return: 返回中间索引
'''
tmp = li[left] # 取最左边的值,作为中间值
while left < right: # 左索引一定要小于右索引,
while left < right and li[right] >= tmp:
# 从后向前找一个小于tmp的元素,找不到就将索引-1向前找
# = tmp可以使right的值是tmp左边的索引
right -= 1
li[left] = li[right] # 找到之后放到最左边 ,此时right位置的值有两个,
while left < right and li[left] <= tmp:
# 在从前往后找一个比tmp大的,找不到就将索引+1向后找
# = tmp可以使right的值是tmp右边的索引
left += 1
li[right] = li[left] # 找到之后放到right位置,
# 当左右索引位置重合时循环结束
li[left] = tmp
return left
def _quick_sort(li, left, right): # 递归
if left < right: # 至少两个元素
mid = partition(li, left, right) # 取中间索引,将两面进行递归
_quick_sort(li, left, mid - 1)
_quick_sort(li, mid + 1, right)
归位图解

堆排序
首先介绍堆:
大根堆:一棵完全二叉树,满足任一节点都比其孩子节点大
小根堆:一棵完全二叉树,满足任一节点都比其孩子节点小
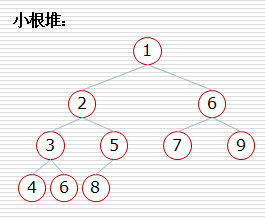

堆的向下调整性质
前提:节点的左右子树都是堆,但是自身不是堆
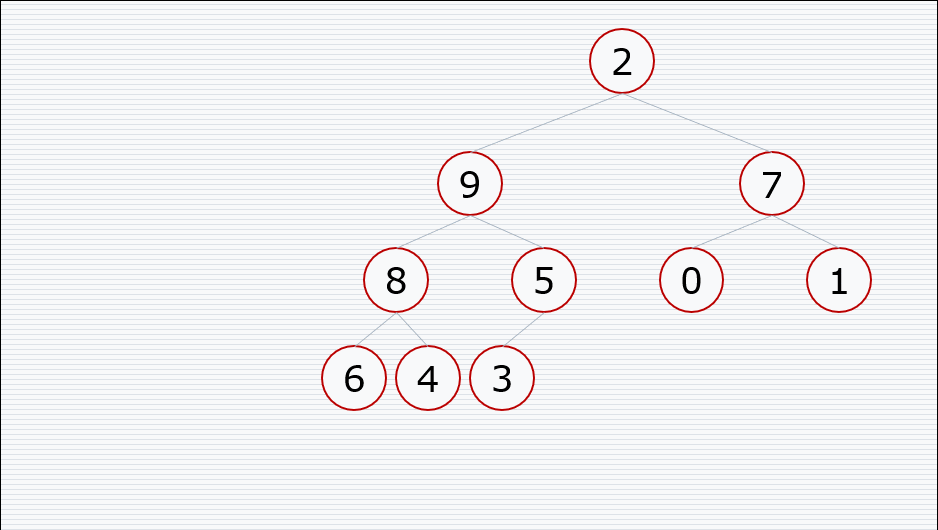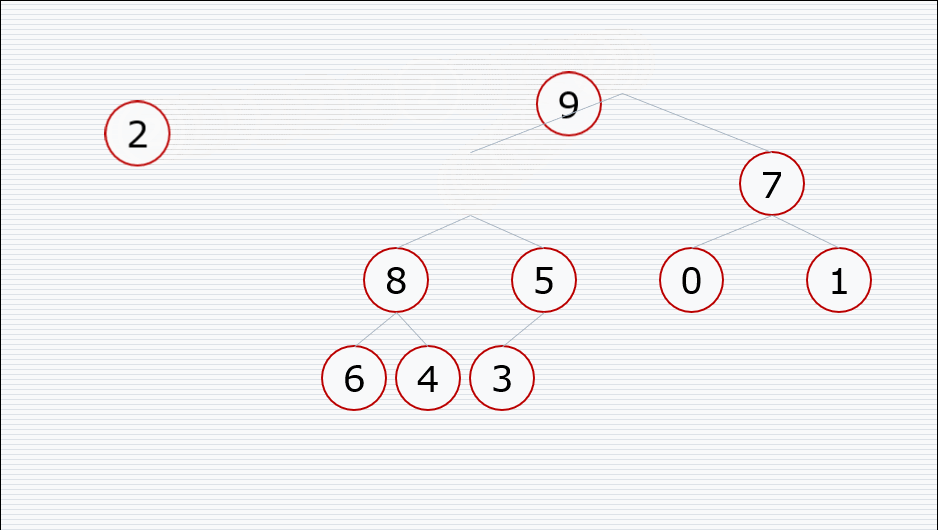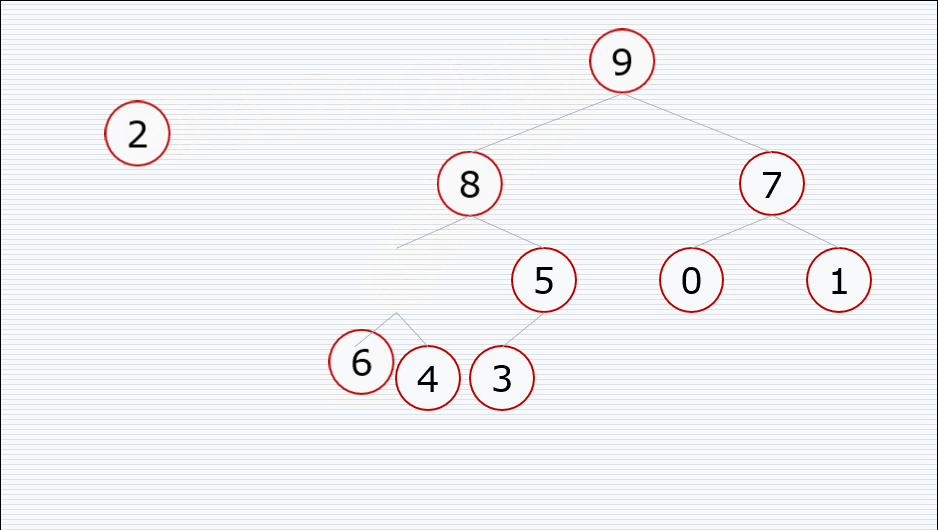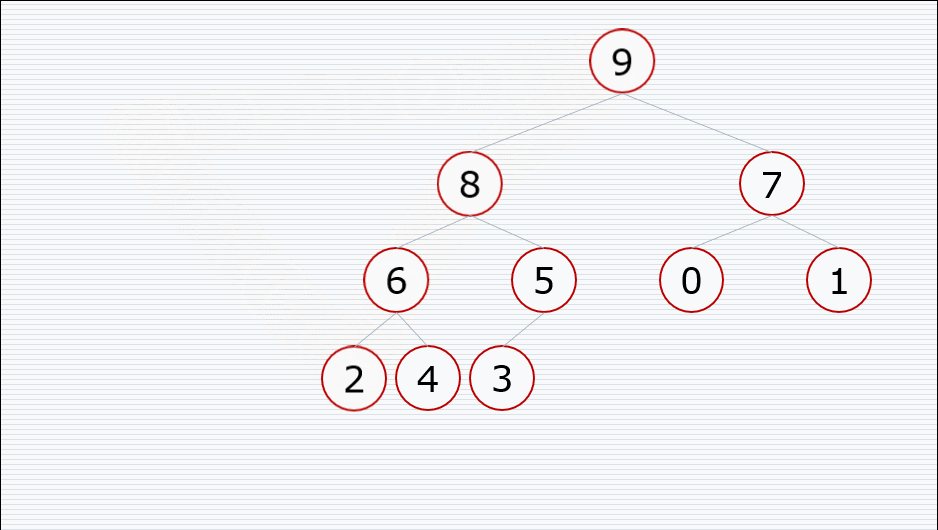
堆排序的过程
建立堆
将列表视为按索引排列的完全二叉树
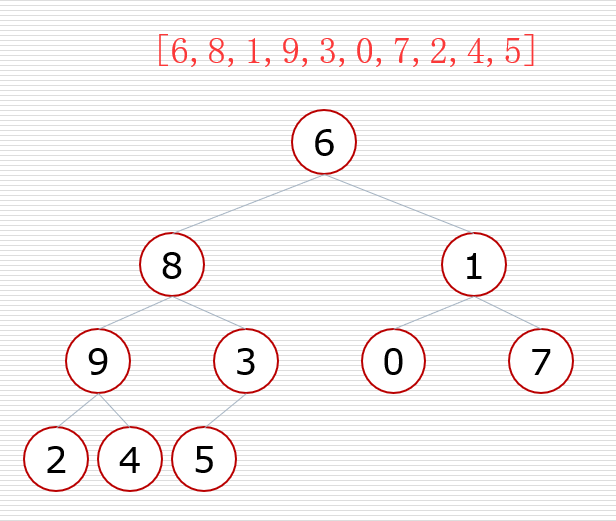
根据堆的向下调整性质,将完全二叉树调整成堆
构造堆时首先从最后一个叶子节点的父节点开始
单节点构造代码
def sift(li, low, high):
'''
:param li: 列表
:param low: 子树根的下标
:param high: 最大索引
:return:
'''
tmp = li[low] # 子树根节点的值
i = low # 子树根下标
j = 2 * i + 1 # 左孩子下标
while j <= high: # 退出条件2:当前i位置是叶子结点,j位置超过了high
# j 只想更大的孩子
if j + 1 <= high and li[j+1] > li[j]:
j = j + 1 # 如果右孩子存在并且更大,j指向右孩子
if tmp < li[j]: # 如果根的值小于孩子节点的值
li[i] = li[j] # 为根节点赋值比较大的元素
# 向下延伸,比较tmp与比较大的叶子节点下面节点之间的关系
i = j
j = 2 * i + 1
else: # 退出条件1:tmp的值大于两个孩子的值
break
# 循环结束后,i的位置可能是个根节点,也可能是个叶子节点,总之他下面的节点都比tmp小
li[i] = tmp
我们可以求出最后一个叶子节点的父节点,此父节点之前的节点都是需要进行排序的,别问我为什么,因为最后一个叶子节点的父节点的后面的节点都没有子节点
n = len(li)
# n是元素个数,n-1就是最后一个叶子节点的索引,他的父节点的索引就是(n-1-1)//2=n//2-1
# 最后一个父节点之前的下标全部需要调整
for i in range(n//2-1, -1, -1):
# i 是建堆时要调整的子树的根的下标
sift(li, i, n-1)
# 上面代码执行完后,一个堆就构造完了
后面就是从堆中取数
for i in range(n-1, -1, -1): #i表示当前的high值 ,也就是无序区的最后一位
# 每次将堆顶的元素放到最后位置,有序区就增加一位,无序区减少一位
li[i], li[0] = li[0], li[i]
# 现在堆的范围 0~i-1,然后调整
sift(li, 0, i-1)
# 取元素,调整,重复
将上两步结合,我们就能将一个列表排序
def heap_sort(li):
n = len(li)
for i in range(n//2-1, -1, -1):
sift(li, i, n-1)
for i in range(n-1, -1, -1):
li[i], li[0] = li[0], li[i]
sift(li, 0, i-1)
归并排序
归并排序采用的也是递归的方式,他的过程是
分解:将列表越分越小,直至分成一个元素
合并:将两个有序(两个单个元素是有序的)的列表归并,列表越来越大
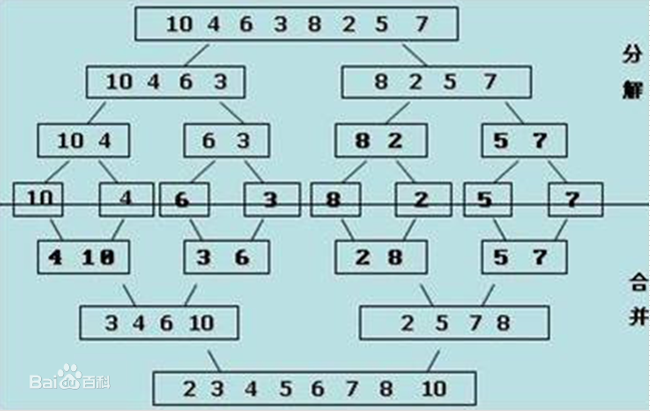
一次归并的过程: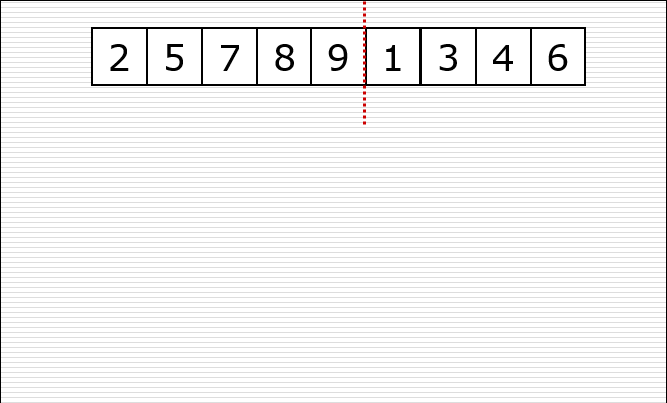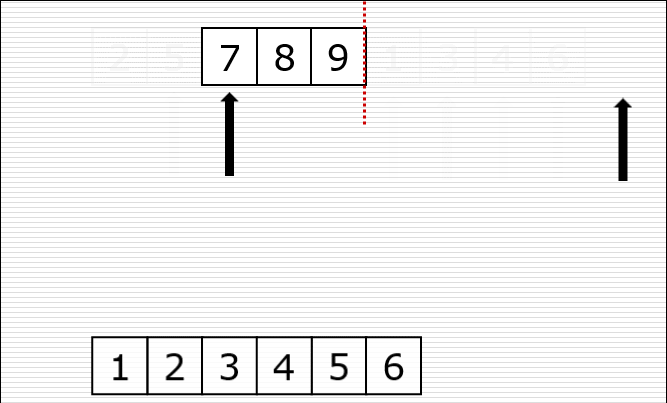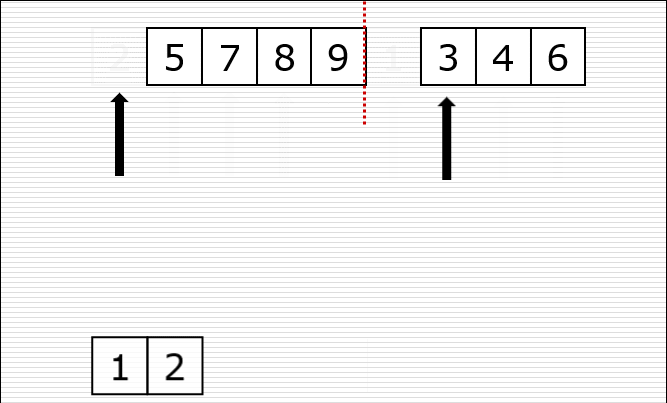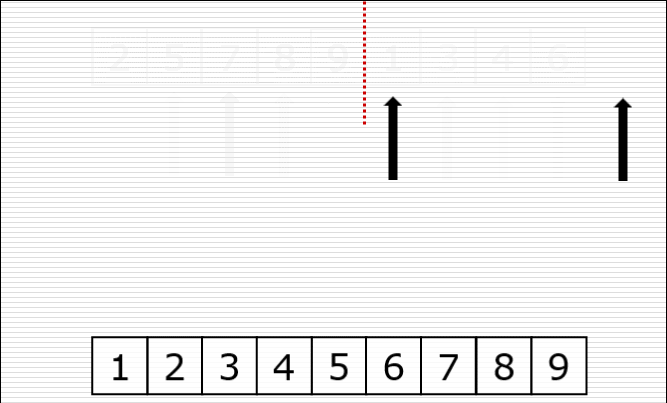
代码实现
def merge(li, low, mid, high):
"""
low~mid有序, mid+1~high有序
:param li: 列表
:return:
"""
i = low # 左箭头
j = mid + 1 # 右箭头
ltmp = []
while i <= mid and j <= high:
# 比较放数,直至其中一个走到尽头
if li[i] < li[j]:
ltmp.append(li[i])
i += 1
else:
ltmp.append(li[j])
j += 1
# 如果i还没到尽头,就把i后的元素都放进去
while i <= mid:
ltmp.append(li[i])
i += 1
# 如果i还没到尽头,就把i后的元素都放进去
while j <= high:
ltmp.append(li[j])
j += 1
# for k in range(low, high+1):
# li[k] = ltmp[k-low]
li[low:high+1] = ltmp # 切片赋值
递归分解
def merge_sort(li, low, high):
if low < high: # 至少有两个元素时递归
mid = (low + high) // 2
merge_sort(li, low, mid) # 左面
merge_sort(li, mid+1, high) # 右面
merge(li, low, mid, high)
希尔排序
希尔排序是一种分组插入排序算法
首先取一个整数a = n/2,将元素分为a个组,每组相邻两元素之间的距离为a,在各组内进行直接插入排序
取第二个整数b = a/2,重复上述分组排序过程,直至n/2=1,即所有的元素在同一组内进行直接插入排序

希尔排序每趟并不会使某些元素有序,而是使整体数据越来越接近有序.最后一趟排序使得所有数据有序
def insert_sort(li): # 插入
for i in range(1, len(li)): # i是摸到的牌的下标,第一个属于有序区,所以从第二个开始
tmp = li[i] # 手里牌的大小
j = i - 1 # j是手里最后一张牌的下标
# 如果tmp大于我手里第j个元素,他就应该放在第j个位置上,如果小于就继续向前比较
while j >= 0 and li[j] > tmp: # 两个终止条件:j小于0表示tmp是最小的 顺序不要乱
# 因为保存了i索引位置的值,所以大于tmp的数都向后移动一位,j自减
li[j+1] = li[j]
j -= 1
li[j+1] = tmp
# 分组插入
def shell_sort(li):
d = len(li) // 2
while d > 0:
insert_sort_gap(li, d)
d = d // 2
计数排序
创建一个列表,用来统计每个数出现的次数
def count_sort(li, max_num): # 列表,及最大元素
count = [0 for i in range(max_num + 1)] # 生成一个具有max_num+1(因为有0)个元素的列表,初始值都为0
for num in li:
count[num] += 1 # li中的number对应count中索引,数字没出现一次就在该位置上+1
i = 0
for num,m in enumerate(count): # num数字,m出现次数
for j in range(m):
li[i] = num
i += 1
在基数排序中如果元素范围很大,但是元素间隔较大,会造成很大的内存开销
桶排序
将一个范围内的元素装入一个桶,并保持桶内元素是有序的(插入入桶)
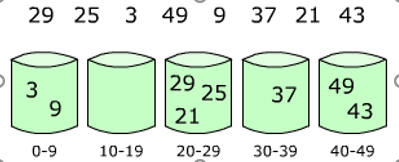
def tong(li,min_num=0,max_num=99,bin_num=10):
'''
:param li:
:param min_num: 最小值
:param max_num: 最大值
:param bin_num: 桶的个数
:return:
'''
bin = [[] for _ in range(bin_num)] #
for num in li:
# +1使最后一个数也能在桶里
n = (max_num-min_num+1)/bin_num # 桶内元素间隔
i = int((num-min_num) // n) # 得到我该放到哪个桶里
bin[i].append(num)
s = len(bin[i])-1
tmp_li = bin[i] # 取得对应桶
tmp = tmp_li[s] # 取最后一个值
j = s-1
while j>=0 and tmp<tmp_li[j]:
tmp_li[j+1] = tmp_li[j]
j = j-1
tmp_li[j+1] = tmp
res = []
for l in bin:
res.extend(l)
return res
基数排序
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。

def list_to_buckets(li, iteration):# 比较装桶
"""
因为分成10个本来就是有序的所以排出来就是有序的。
:param li: 列表
:param iteration: 装桶是第几次迭代
:return:
"""
buckets = [[] for _ in range(10)]
for num in li:
digit = (num // (10 ** iteration)) % 10
buckets[digit].append(num)
return buckets
def buckets_to_list(buckets):#出桶
li = []
for bucket in buckets:
for num in bucket:
li.append(num)
return li
def radix_sort(li):
maxval = max(li) # 10000
it = 0
while 10 ** it <= maxval:#这个是循环用来,在以前一次排序的基础上在排序。
li = buckets_to_list(list_to_buckets(li, it))
it += 1
return li
取一个数的个十百千位
# 个位 i % 10 # 十位 ,先整除10,再去余 i // 10 %10 # 百位 i // 100 %10
各种排序算法的时间复杂度
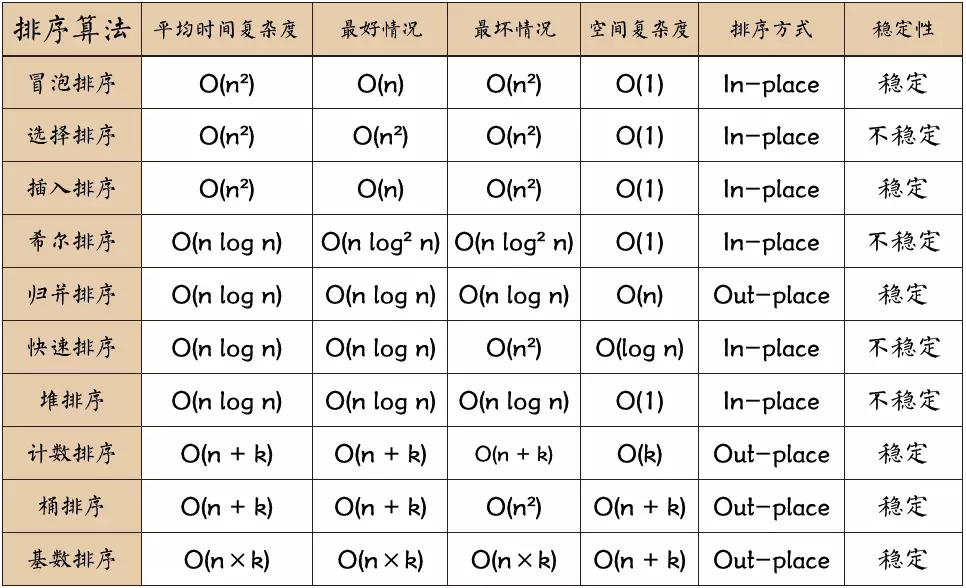
稳定性:排序后 2 个相等键值的顺序和排序之前它们的顺序相同


