稀疏分解中的MP与OMP算法
!!今天发现一个重大问题,是在读了博主的正交匹配追踪(OMP)在稀疏分解与压缩感知重构中的异同,http://blog.csdn.net/jbb0523/article/details/45100659之后一脸懵逼,CS中的稀疏表示不就是把信号转换到另一个变换域中吗?怎么跑出来一个稀疏分解里面又有MP和OMP算法!!后来发现原来稀疏分解先于压缩感知提出,信号稀疏表示的目的就是在给定的超完备字典中用尽可能少的原子来表示信号,可以获得信号更为简洁的表示方式,从而使我们更容易地获取信号中所蕴含的信息,更方便进一步对信号进行加工处理,如压缩、编码等。后面的学者用稀疏分解的思想应用于压缩感知重构中。其实两者解决的问题是一样的。
从数学模型来入手分析这个问题:
所不同的是,在稀疏分解中θ是事先不存在的,我们要去求一个θ用Aθ近似表示y,求出的θ并不能说对与错;在压缩感知中,θ是事先存在的,只是现在不知道,我们要通过某种方法如OMP去把θ求出来,求出的θ应该等于原先的θ的,然后可求原信号x=Ψθ。
1.冗余字典与稀疏表示
2.字典非线性近似
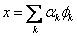
 即对于正交原子,为投影到由φk张成的子空间上的幅值。
即对于正交原子,为投影到由φk张成的子空间上的幅值。3.MP算法

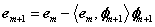

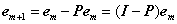
注意矩阵P每次迭代都是不同的。
》提出一个问题
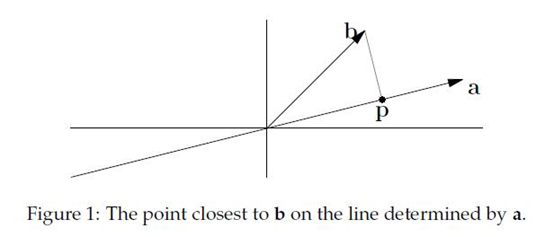
文献[3]中与文献[1]中所表示的算法流程符号略有不同,但意思是一样的,由于要借鉴这篇文章来解释上述提出的问题,所以先简要介绍一下该文献中所说明的MP的算法流程。
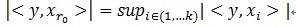 (sup为上确界)r0表示一个字典矩阵的列索引。这样,信号y就被分解为在最匹配原子
(sup为上确界)r0表示一个字典矩阵的列索引。这样,信号y就被分解为在最匹配原子 。
。 
(2)对残值R1f进行步骤[1]同样的分解,那么第K步可以得到:
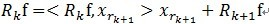 , 其中
, 其中 满足
满足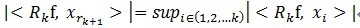 。(在别的参考文献中有形如这样的形式
。(在别的参考文献中有形如这样的形式![]() ,之前没有搞明白,其实也就是移项了而已)可见,经过K步分解后,信号y被分解为:
,之前没有搞明白,其实也就是移项了而已)可见,经过K步分解后,信号y被分解为: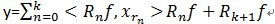 ,其中
,其中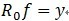 。
。
我们要对信号进行稀疏表示,即在字典中找到一组最适合描述信号的基,把信号表示成这组基的线性组合。那为什么会造成不正交呢?举个例子说明一下:在二维空间上,有一个信号y被D=[x1, x2]来表达,MP算法迭代会发现总是在x1和x2上反复迭代,即 ,这个就是信号(残值)在已选择的原子进行垂直投影的非正交性导致的。再用严谨的方式描述可能容易理解:在Hilbert空间H中,
,这个就是信号(残值)在已选择的原子进行垂直投影的非正交性导致的。再用严谨的方式描述可能容易理解:在Hilbert空间H中, ,
,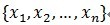 ,定义
,定义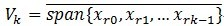 ,就是它是这些向量的张成的一个空间,MP构造一种表达形式:
,就是它是这些向量的张成的一个空间,MP构造一种表达形式:
这里的Pvf表示 f在V上的一个正交投影操作,那么MP算法的第 k 次迭代的结果可以表示如下(前面描述时信号为y,这里变成f了,请注意):

如果fk是最优的k项近似值,当且仅当![]() 。由于MP仅能保证
。由于MP仅能保证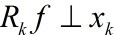 ,所以
,所以fk一般情况下是次优的。这是什么意思呢?fk是k个项的线性表示,这个组合的值作为近似值,只有在第k个残差和fk
正交,才是最优的。如果第k个残值与fk
正交,意味这个残值与fk的任意一项都线性无关,那么第k个残值在后面的分解过程中,不可能出现fk中已经出现的项,这才是最优的。而一般情况下,不能满足这个条件,MP一般只能满足第k个残差和xk正交,这也就是前面为什么提到“信号(残值)在已选择的原子进行垂直投影是非正交性的”的原因。如果第k个残差和fk不正交,那么后面的迭代还会出现fk中已经出现的项,很显然fk就不是最优的,这也就是为什么说MP收敛就需要更多次迭代的原因。不是说MP一定得到不到最优解,而且其前面描述的特性导致一般得到不到最优解而是次优解。那么,有没有办法让第k个残差与fk
正交,方法是有的,这就是下面要谈到的OMP算法。
4.OMP算法
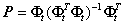
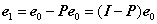
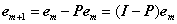
其中I为单位阵。需要注意的是在迭代过程中Φt为所有被选择过的原子组成的矩阵,因此每次都是不同的,所以由它生成的正交投影算子矩阵P每次都是不同的。
(5)直到达到某个指定的停止准则后停止算法。


那么具体在OMP算法中是如何体现的?
文献[4]中给出了施密特(Schimidt)正交化的过程:

上面的的[x,y]表示向量内积,[x,y]=xTy=yTx=[x,y]。施密特正交化公式中的br实际上可写为:
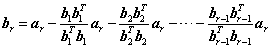 分子之所以可以这么变化是由于[x,y]实际上为一个数,因此[x,y]x=x[x,y]= xxTy。
分子之所以可以这么变化是由于[x,y]实际上为一个数,因此[x,y]x=x[x,y]= xxTy。
首先给出一个结论:
设OMP共从冗余字典中选择了r个原子,分别是a1,a2,……,ar,根据正交匹配追踪的流程可以知道待分解信号x最后剩余的残差eromp为
 (式1)
(式1)
该残差也可以表示为
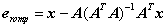 (式2)
(式2)
其中矩阵A为选择的r个原子组成的矩阵,e(r-1)omp为选择(r-1)个原子时的残差。
将选择的r个原子a1,a2,……,ar进行施密特正交化:

则残差eromp还可以写为
 (式3)
(式3)
(式1)一般出现在稀疏分解算法中,(式2)一般出现在重构算法中,(式3)是自己琢磨出来的(受到沙威的文档中提到的施密特正交化的启发,但沙威只限于向量情况下,详情可参见[6],此处相当于一个推广)
OMP分解过程,实际上是将所选原子依次进行Schimidt正交化,然后将待分解信号减去在正交化后的原子上各自的分量即可得残差。其实(式3)求残差的过程也是在进行施密特正交化。
有个关键问题还是要说的,分解后在所选择各原子上的系数是多少呢?答案其实也很简单,各个系数是(ATA)-1ATx,即最小二乘解,这个解是一个列向量,每一个元素分别是组成矩阵A的各原子的线性组合系数,这个在《正交匹配追踪(OMP)在稀疏分解与压缩感知重构中的异同》也会明确再次说明。
同理,若设MP共从冗余字典中选择了r个原子,分别是a1,a2,……,ar,根据匹配追踪的流程可以知道待分解信号x每次迭代后剩余的残差ermp为
 比较式(3)的第2个等号表示的eromp与此处的ermp也可以体会出OMP与MP的区别吧。
比较式(3)的第2个等号表示的eromp与此处的ermp也可以体会出OMP与MP的区别吧。
参考文献:
[1] 彬彬有礼.稀疏表示与匹配追踪,http://blog.csdn.net/jbb0523/article/details/45099655
[2] 了凡春秋. Matlab匹配追踪(Matching Pursuit) 之一,https://chunqiu.blog.ustc.edu.cn/?p=634
[3] 逍遥剑客. MP算法和OMP算法及其思想,http://blog.csdn.net/scucj/article/details/7467955
[4] 同济大学数学系. 线性代数(第五版)[M].高等教育出版社,2007:114.
[5] 彬彬有礼. 施密特(Schimidt)正交化与正交匹配追踪,http://blog.csdn.net/jbb0523/article/details/45100351
[6] 沙威. “压缩传感”引论.http://www.eee.hku.hk/~wsha/Freecode/Files/Compressive_Sensing.pdf


