图

 

1学习总结

（1）掌握图的相关概念

（2）理解图的储存结构，包括邻接矩阵储存和邻接表储存。

（3）图的遍历，掌握深度优先遍历和广度优先遍历。

（4）学会图的其他算法，普里姆算法和克鲁斯卡尔算法，狄克斯特拉算法和弗洛伊德算法，并学会拓扑排序。

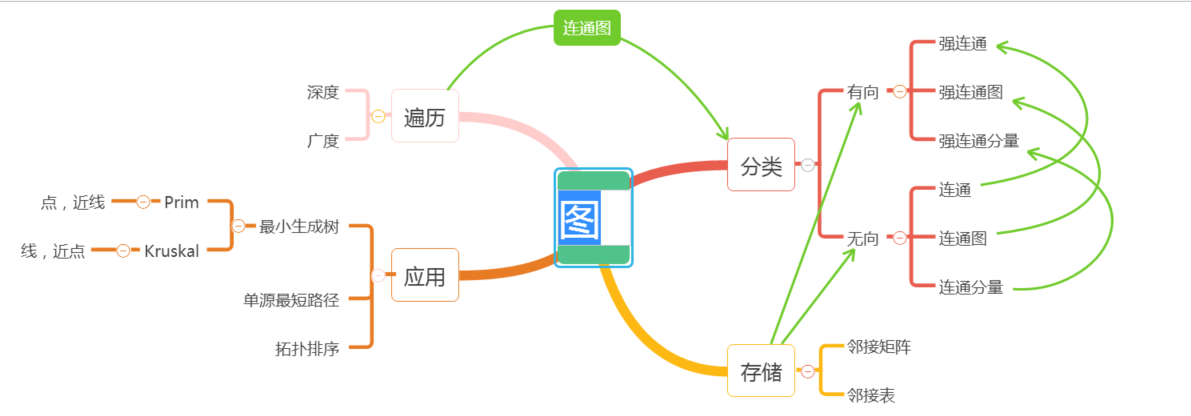
1.1图的思维导图

 

2.PTA实验作业

1.1 题目1：7-1 图着色问题

1.2 设计思路

1用邻接矩阵来处理

　　子函数　　

　　if vis[i]=false || flag=false

　　结束

　　vis[i]=true

　　但颜色一样且改点为顶点时

　　flag=0

　　return

　　else该点是顶点 visit[j]=false

　　递归

　　　主函数

　　　先把数据存入邻接矩阵中

　 　　for (i=0;i<n;i++)一共循环n次

　　　　set<int>s;创建集合s

  　　for (int j = 0; j < v; j++)

　　　　输入颜色c

　　　　用insert（）将存入集合s中

　　　　把颜色存入color集合；

　　　　if s中元素个数不等于k

　　　　flag=false

　　　　else

　　　　用memset函数将vis数组全部替换为false

　　　　for j=0 j<v;j++

　　　　　isyes(j)

　　　　if flag=false

　　　　退出循环

　　　　if flag=true

　　　　输出yes

　　　　else

　　　　输出no

 

　　使用c++中的set和memset简化程序。必须颜色的 个数等。

　　遇到的问题，对set和memset函数掌握不熟练，容易出差

　　

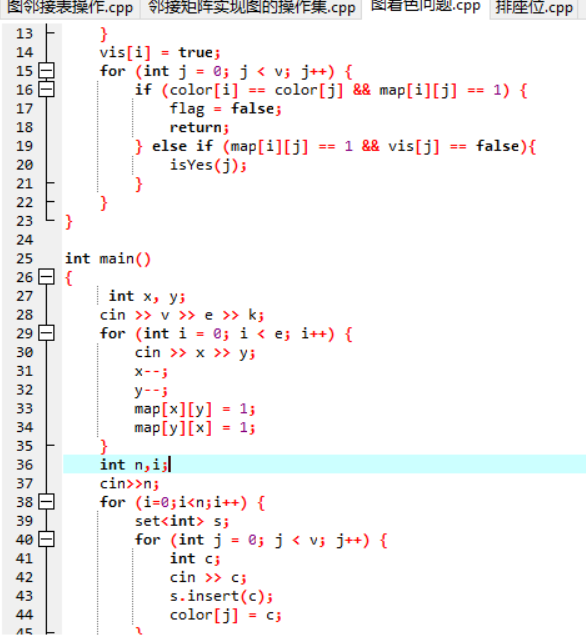
1.3 代码截图

1.4 PTA提交列表说明

　　不能熟练使用set和memset导致编译错误

 

2.1 题目2：7-2 排座位

2.2 设计思路

　　init

　　创建一个　father数组使得顶点数与数组值对应

　　combine

　　判断是否有公共朋友或者为朋友

　　如果有共同朋友或者互相为朋友

　　取两者中大的顶点

　　　使其father=小的那个

　　else为敌人

　　存入map数组中，值为-1

　　　find　

　　　　if(x!=father[x]) father[x]=finds(father[x]);
　　　　return father[x];

　　主函数

　　　init（）

　　　meeset函数将maps中的值全部变为0

　　　for(int i=1;i<=m;i++)

　　　输入关系，并运行combine()子函数

　　　for(循环k次)

　　　根据finds函数判断

　　　　

　　

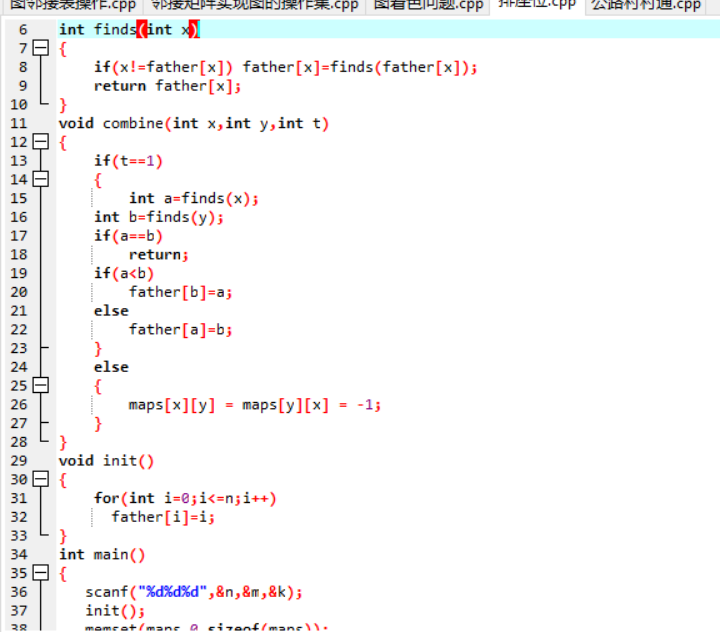
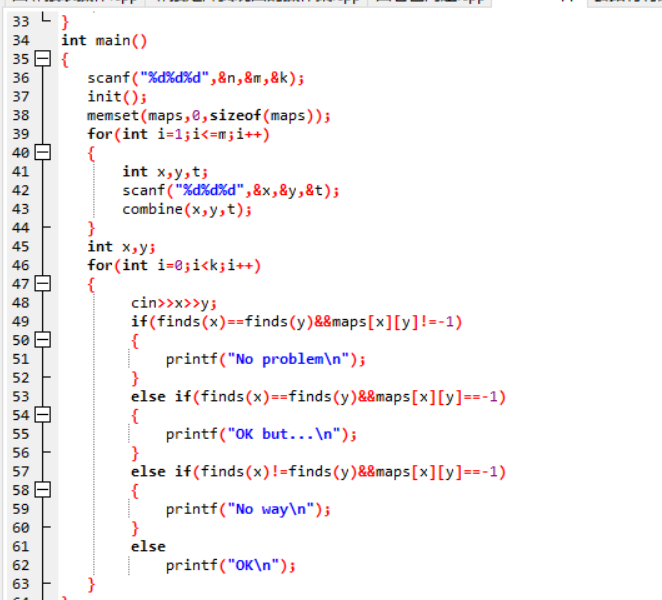
2.3 代码截图

 

 

 

 

 

2.4 PTA提交列表说明

 

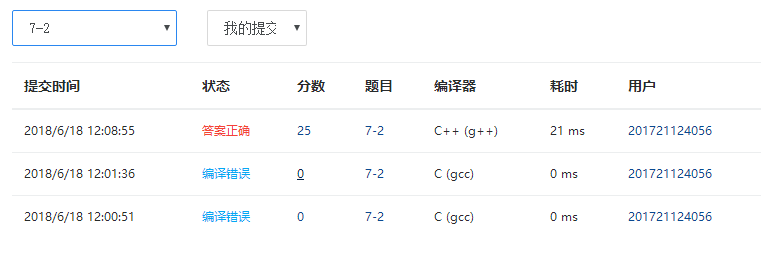
　　函数的使用有问题

 

 

　　2.1 题目3：7-4 公路村村通

　　2.2 设计思路

 　　这题用Prim算法生成最小生成树，通过判断最终最小生成树的结点个数是否为顶点个数（即边数为顶点个数-1），如果是，则可以生成最小生成树，能够做到村村通，如果不是，则不行。 

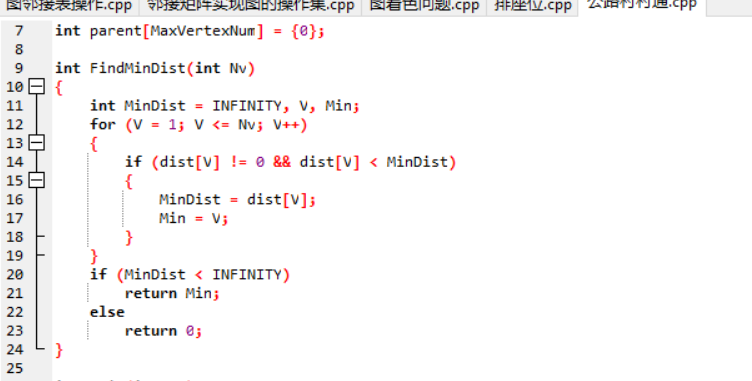
　　　　FindMinDist（）用来寻找未被收录的当前最短路径的顶点下标

　　　　for (V = 1; V <= Nv; V++)

　　　　if (dist[V] != 0 && dist[V] < MinDist)

　　　　如果节点V未被收录(为0表示被收录)并且小于最短距离

　　　　MinDist = dist[V]; // 更新最短距离

　　　　Min = V; // 设置V的父亲结点为0

　　　　

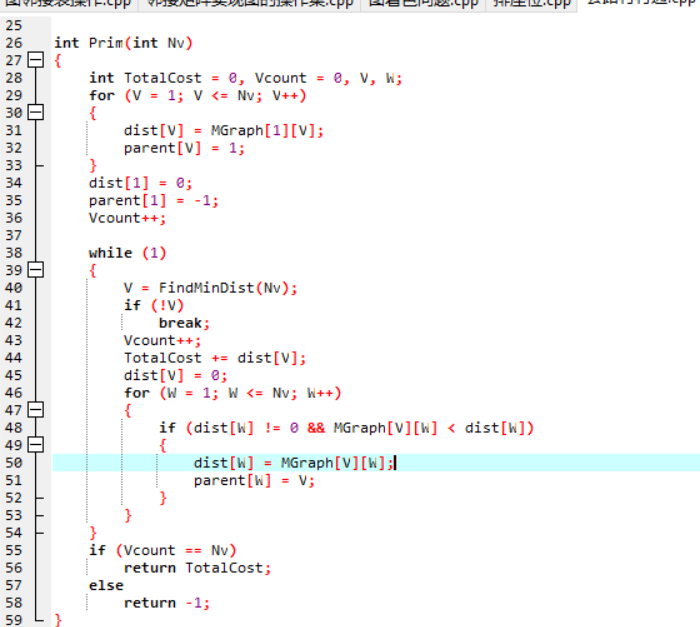
　　　　prim（）

　　　　使用prim算法生成最小生成树

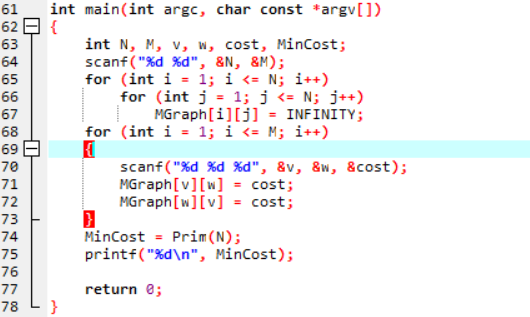
　　　　主函数

　　　　int main

　　　　初始化图

　　　　输入信息

　　　　MinCost = Prim(N);

　　　　 printf("%d\n", MinCost);

　　2.3 代码截图

 

 

 

 

 

 

 

 

2.4 PTA提交列表说明

 

 　　输入数据不足以保持通畅没有考虑

3.截图本周题目集的PTA最后排名

3.1 PTA排名

3.2 我的总分：

 

 

4. 阅读代码

 #include <stdio.h>
 #define MAXLENTH 50
 #define MAX 9999

void Dijkstra(int n, int v, int *dist, int *prev, int c[MAXLENTH][MAXLENTH])
{
 
    bool s[MAXLENTH];    
 int i,j;
    for(i=1; i<=n; ++i)
    {
        dist[i] = c[v][i];
  
        s[i] = false;    
        if(dist[i] == MAX)
            prev[i] = 0;
        else
            prev[i] = v;
    }
    dist[v] = 0;
    s[v] = true;
 
   
    for(i=2; i<=n; ++i)
    {
        int t = MAX;
        int u = v;
       
        for(j=1; j<=n; ++j)
            if((!s[j]) && dist[j]<t)
            {
               
                 u = j;            
                t = dist[j];
            }
   
        s[u] = true;    
 
       
        for(j=1; j<=n; ++j)
            if((!s[j]) && c[u][j]<MAX)
            {
                int newdist = dist[u] + c[u][j];
                if(newdist < dist[j])
                {
                    dist[j] = newdist;
                    prev[j] = u;
                }
            }
    }
}
 
void searchPath(int *prev,int v, int u)
{
    int que[MAXLENTH];
    int tot = 1;
    que[tot] = u;
    tot++;
    int tmp = prev[u];
    while(tmp != v)
    {
        que[tot] = tmp;
        tot++;
        tmp = prev[tmp];
    }
    que[tot] = v;
    for(int i=tot; i>=1; --i)
        if(i != 1)
   printf("%d -> ",que[i]);
        else
            printf("%d\n",que[i]);
}
 
int main()
{
    int dist[MAXLENTH];     // 表示当前点到源点的最短路径长度
    int prev[MAXLENTH];     // 记录当前点的前一个结点
    int c[MAXLENTH][MAXLENTH];   // 记录图的两点间路径长度
    int n, r;             // 图的结点数和路径数
 int p, q, len;          // 输入p, q两点及其路径长度
 int i,j;
 
    // 输入结点数
 printf("please input the num of the point:");
 scanf("%d",&n);
    // 输入路径数
 printf("please input the num of the edge:");
 scanf("%d",&r);
   
 
    // 初始化c[][]为MAX
    for(i=1; i<=n; ++i)
        for(int j=1; j<=n; ++j)
            c[i][j] = MAX;
 
    for(i=1; i<=r; ++i) 
    {
        printf("please input the value of the %dth edge:",i);
  scanf("%d %d %d",&p,&q,&len);

  
        if(len < c[p][q])      
        {
            c[p][q] = len;      // p指向q
            c[q][p] = len;      // q指向p，这样表示无向图
        }
    }
 
    for(i=1; i<=n; ++i)
        dist[i] = MAX;
    for(i=1; i<=n; ++i)
    {
        for(j=1; j<=n; ++j)
            printf(" ", c[i][j]);
        printf("\n");
    }
 
    Dijkstra(n, 1, dist, prev, c);
 
   
 printf("the shortest route length is :%d\n",dist[n]);
 
 printf("the first piont to the last point route:");
    searchPath(prev, 1, n);
}

 

Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解，但由于它遍历计算的节点很多，所以效率低。

　　其基本思想是，设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。

初始时，S中仅含有源。设u是G的某一个顶点，把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径，并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u，将u添加到S中，同时对数组dist作必要的修改。一旦S包含了所有V中顶点，dist就记录了从源到所有其它顶点之间的最短路径长度。