[珠玑之椟]字符串和序列：左移、哈希、最长重复子序列的后缀数组解法、最大连续子序列

　　字符串和数组在存储上是类似的，把它们归为同一主题之下。本文主要介绍三大类问题和它们衍生的问题，以及相应算法。

　　本文主要介绍和讨论的问题和介绍的算法（点击跳转）：

 

字符串循环移位(左旋转)问题

问题叙述：

　　将一个n元一维向量向左旋转i个位置。例如，当n=8且i=3时，"abcdefgh"旋转为"defghabc"，要求时间为O(n)，额外存储占用为O(1)。（《编程珠玑》第二章问题B）

分析：

　　严格来说这并不是一个字符串，因为'\0'是不会移动的。为了叙述方便，可以把它认为是字符串，只是不对'\0'进行操作罢了。

　　如果不考虑时间要求为O(n)，那么可以每次整体左移一位，一共移动i次。只使用O(1)的空间的条件下，一共要进行元素交换O(n*i)次；

　　如果不考虑空间要求为O(1)，那么可以把前i个存入临时数组，剩下的左移i位，再把临时数组里的内容放入后i个位置中。

　　很可惜，由于两个限制条件，以上两种思路都不满足要求。

　　对于算法1和算法2，如果理解有困难，不必强求，能掌握算法3就好。

 

算法1：“杂技”代码

　　为了满足O(1)空间的限制，延续第一个思路，如果每次直接把原向量的一个元素移动到目标向量中它的应该出现新位置上就行了。先把array[0]保存起来，然后把array[i]移动到array[0]上，array[2i]移到array[i]上，直至返回取原先的array[0]。但这需要解决的问题是，如何保证所有元素都被移动过了？数学上的结论是，依次以array[0],...,array[gcd(i,n)-1]为首元进行循环即可，其中gcd(a,b)是a与b的最大公约数。因此算法可写为：

int vec_rotate(char *vec,int rotdist, int length) {
    int i,j,k,times;
    char t;
    times = gcd(rotdist,length);
    printf("%d\n",times);
    for(i=0;i<times;i++) {
        t = vec[i];
        j = i;
        while(1) {
            k = j+ rotdist;
            if(k>=length)
                k-=length;
            if(k==i)
                break;
            vec[j] = vec[k];
            j = k;
        }
        vec[j]=t;
    }
    return 0;
}
向量左旋算法1:"杂技"代码

　　正如“杂技”一词所暗示的一样，这个算法就像在玩杂耍球，你要让它们中的每一个都在合适的位置上，这些球，除了手中有一个，其它几个都在空中。如果不熟悉，很容易手忙脚乱，把球掉的满地都是。

 

算法2：块交换

　　考虑第二个思路，相当于把向量x分为两部分a和b，左移就是把ab变成ba，其中a包含了前i个元素。假设a比b短，把b分为bl和br，那么需要先把a与br交换得到brbla，再对brbl递归左旋。而a比b长的情况类似，当a与b长度相等时直接两两交换元素就能完成。同时可以看到，每次待交换的向量长度都小于上一次，最终递归结束。

int vec_rotate_v1(char *vec,int i, int length)
{
    int j = length - i;
    if(i>length)
        i = i%length;
    if(j==0)
        return 0;
    else if(j>i) {
    //case1: ab -> a-b(l)-b(r)
        swap(vec,0,j,i);
        vec_rotate_v1(vec,i,j);
    }    
    //case2: ab -> a(l)-a(r)-b
    //i becomes less
    else if(j<i)    {
        swap(vec,i,2*i-length,j);
        vec_rotate_v1(vec,2*i-length,i);
    }
    else
        swap(vec,0,i,i);
    return 0;
}

int swap(char* vec,int p1,int p2, int n) {
    char temp;
    while(n>0) {
        temp    = vec[p1];
        vec[p1] = vec[p2];
        vec[p2] = temp;
        p1++;
        p2++;
        n--;
    }
    return 0;
}
向量左旋算法2：块交换

　　这个算法的缺陷是，需要对三种情况进行讨论，而且下标稍不注意就会出错。

 

算法3：求逆（推荐）

　　延续算法2的思路，并假定有一个辅助函数能对向量求逆。这样，分别对a、b求逆得到arbr，再对整体求逆便获得了ba！难怪作者也要称之为“灵光一闪”的算法。可能以前接触过矩阵运算的读者对此很快便能理解，因为(ATBT)T = BA。算法如下：

int vec_rotate_v2(char *vec,int i,int length){
    assert((i<=0)||(length<=0))
    if(i>length)
        i = i%length;
    if (i==length) {
        printf("i equals n. DO NOTHING.\n");
        return 0;
    }
    reverse(vec,0,i-1);
    reverse(vec,i,length-1);
    reverse(vec,0,length-1);
    return 1;
}

int reverse(char *vec,int first,int last){
    char temp;
    while(first<last){
        temp = vec[first];
        vec[first] = vec[last];
        vec[last] = temp;
        first++;
        last--;
    }
    return 0;
}
向量左旋算法3：求逆

　　如果能想到，算法3无疑既高效，也难以在编写时出错。有人曾主张把这个求逆的左旋方法当做一种常识。

　　来看看这种思想的应用吧：

扩展：(google面试题)用线性时间和常数附加空间将一篇文章的所有单词倒序。

举个例子：This is a paragraph for test

处理后： test for paragraph a is This

如果使用求逆的方式，先把全文整体求逆，再根据空格对每个单词内部求逆，是不是很简单？另外淘宝今年的实习生笔试有道题是类似的，处理的对象规模比这个扩展中的“一篇文章”小不少，当然解法是基本一样的，只不过分隔符不是空格而已，这里就不重述了。

 

以字符串散列为例的哈希表

　　关于哈希表，这里就不做解释了，主要是演示一个基于哈希表的用于单词计数的程序。

typedef struct node *nodeptr;
typedef struct node {
    char *word;
    int count;
    nodeptr next;
} node;
哈希表中的结点
#define NHASH 29989
//在宽松“单词”的定义下《圣经》里也只有29131个不同的单词
//与之可能数接近的质数
#define MULT 31//乘数
nodeptr bin[NHASH];
参数选择和哈希表头
unsigned int hash(char *p) {
    unsigned int h = 0;
    for(;*p;p++)
        h = MULT *h +*p;
    return h%NHASH;
}
字符串常用的哈希函数
void incword(char *s) {
    nodeptr p;
    int h= hash(s);
    for(p=bin[h];p!=NULL;p=p->next)
        if(strcmp(s,p->word)==0) {
            (p->count)++;
            return;
        }
    p = malloc(sizeof(node));
    p->count = 1;
    p->word = malloc(strlen(s)+1);
    strcpy(p->word,s);
    p->next = bin[h];
    bin[h] = p;
}
单词计数函数
int main(void) {
    int i;
    nodeptr p;
    char buf[100];
    for(i=0;i<NHASH;i++)
        bin[i] = NULL;
    while(scanf("%s",buf)!=EOF)
        incword(buf);
    for(i=0;i<NHASH;i++)
        for(p=bin[i];p!=NULL;p=p->next)
            printf("%s\t%d\n",p->word,p->count);
    return 0;
}
主程序

 

最长重复子序列问题的后缀数组解法

　　最长重复子序列问题除了使用穷举法，还可以使用后缀数组和后缀树来求解。这里给出使用后缀数组解决的最长重复子序列的过程，并以“banana”为例进行演示。首先写下一个比较两个字符串从头开始共同部分的长度的函数：

int comlen(char *p, char *q) {
    int i = 0;
    while(*p&&(*p++ == *q++))
        i++;
    return i;
}
comlen

　　设定该程序最多处理MAXN个字符，并存放在数组c中，a是对应的后缀数组：

#define MAXN 5000000
char c[MAXN],*a[MAXN];

　　读取输入时，对a进行初始化：

//n是已读入的字符数目
int input(int n) {
    int ch;
    while((ch = getchar())!=EOF) {
        a[n] = &c[n];
        c[n++] = ch;
    }
    c[n] = 0;
    return n;
}

　　这样，对于“banana”，对应的后缀数组为：

　　a[0]:banana

　　a[1]:anana

　　a[2]:nana

　　a[3]:ana

　　a[4]:na

　　a[5]:a

　　它们是"banana"的所有后缀，这也是“后缀数组”命名原因。

　　如果某个长字符串在数组c中出现了两次，那么它必然出现在两个不同的后缀中，更准确的说，是两个不同后缀的同一前缀。通过排序可以寻找相同的前缀，排序后的后缀数组为：

a[0]:a

a[1]:ana

a[2]:anana

a[3]:banana

a[4]:na

a[5]:nana

　　扫描排序后的数组的相邻元素就能得到最长的重复字串，本例为“ana”。

　　这里做一个扩展：（习题16.8）如何寻找至少出现过n次的最长重复子序列？

　　解法是比较a[i...i+n]中第一个和最后一个的最长公共前缀长度，上文是对n=1的特例。因此写出一般化的扫描函数：

int scan(int n,int k) {
    int maxi=0,i;
    int temp,maxlen = 0;
    for(i=0;i<n-k;i++) {
        temp = comlen(a[i],a[i+k]);
        if(temp>maxlen) {
            maxlen = temp;
            maxi = i;
        }
    }
    printf("%d times the longest:%.*s\n",k,maxlen,a[maxi]);
    return 0;
}

　　以及主程序：

int pstrcmp(char **p, char **q)
{   return strcmp(*p, *q); }


int main(void) {
    int i,n;
    n = input(0);
    qsort(a,n,sizeof(char *),pstrcmp);
    printf("\n");
    for(i=0;i<n;i++)
        printf("%s\n",a[i]);
    scan(n,1);
    scan(n,2);
    return 0;
}

　　这种后缀数组排序的方法同样可以解两个字符串最长公共字符串的问题，如习题15.6和习题15.9。

 

最大连续子序列

基本问题：

　　（《编程珠玑》第八章，同样的问题见于《编程之美》2.14节）输入是具有n个浮点数的向量x，输出时输入向量的任何连续子向量的最大和。为了避免不能处理最大和小于0的情况，这里直接把习题8.9的处理方法拿来，将最大和初值设为一个很小的负数，这里用NI表示。同时为了简单起见，这里的数组使用int型而不是要求的浮点型表示，maxsum()用于求两个数的最大值。

1.直接解法

　　最直接的方式是遍历所有可能的连续子向量，用i和j分别表示向量的首元和最后的尾元，k表示真实的尾元：

int max_array_v1(int *array,int length)
{
    int sum,maxsofar = NI;
    int i,j,k;
    for(i=0;i<length;i++)
        for(j=i;j<length;j++) {
            sum = 0;
            for(k=i;k<=j;k++) {
                sum += array[k];
                maxsofar = maxnum(maxsofar,sum);
            }
        }
    return maxsofar;
}

2.O(n2)的解法

　　第1种方法的代码具有显而易见的浪费：对于一个子序列可能重复计算了多次。并且具有O(n3)的时间复杂度。其实k是多余的，依靠首尾两个变量i、j足以表示一个子向量。同时，j增长时，可以直接使用上一次的计算和与新增元素相加。因此改写为：

int max_array_v2_1(int *array,int length)
{
    int sum,maxsofar = NI;
    int i,j;
    for(i=0;i<length;i++) {
        sum = 0;
        for(j=i;j<length;j++) {
            sum += array[j];
            maxsofar = maxnum(maxsofar,sum);
        }
    }
    return maxsofar;
}

　　另外一方面，由这个避免重复计算累加和的角度出发，构造一个累加和数组cumarr，cumarr[i]表示array[0...i]各个数的累加和，这样，array[i...j]的和就可以用cumarr[j]-cumarr[i-1]来表示了。考虑到边界值，令cumarr[-1]=0，（习题8.5）在C中的做法是令cumarr指向一个数组的第1个元素，cumarr = recumarr +1。有了cumarr[]就可以遍历所有的i、j来求最大值了：

int max_array_v2_2(int *array,int length)
{
    int sum,maxsofar;
    int i,j;
    int *realcumarr,*cumarr;
    realcumarr = (int *)malloc((length+1)*sizeof(int));
    if(realcumarr == NULL)
        return -1;
    cumarr = realcumarr + 1;
    cumarr[-1] = 0;
    for(i=0;i<length;i++)
        cumarr[i] = cumarr[i-1] + array[i];
    maxsofar = NI;
    for(i=0;i<length;i++)
        for(j=i;j<length;j++) {
            sum = cumarr[j] - cumarr[i-1];
            maxsofar = maxnum(maxsofar,sum);
        }
    return maxsofar;
}

　　虽然这个累加和数组的解法与后面两个相比，时间复杂度远不是最优的，然而这种数据结构很有用，在后面会看到这一点。

 

3.分治法(nlogn)

　　分治法的基本思想是，把n个元素的向量分成两个n/2的子向量，递归地解决问题再把答案合并。

　　分容易，合并就要花点心思了。因为对于初始大小为n的向量，它的最大连续子向量可能整体在分成的两个子向量中之一，也可能跨越了两个子向量。每次合并都需要计算这个跨越分界点的最大连续子向量，占据了很大的开销。

int max_array_v3(int *array,int l,int u)
{
    int i,m;
    int lmax,rmax,sum;
    lmax = rmax = NI;
    if(l>u)
        return 0;
    else if(l == u)
        return maxnum(NI,array[l]);
    m = (l+u)/2;
    sum = 0;
    for(i=m;i>=1;i--) {
        sum += array[i];
        lmax = maxnum(sum,lmax);
    }
    sum = 0;
    for(i=m+1;i<=u;i++) {
        sum += array[i];
        rmax = maxnum(sum,rmax);
    }
    return maxnum(lmax+rmax,maxnum(max_array_v3(array,l,m),max_array_v3(array,m+1,u)));
}

　　这种解法使我联想到了《算法导论》用分治法求解最近点对的问题：通过将区域划分成两个子区域，递归地求解。然而合并时更加复杂：对于左边区域和右边区域获得的最近距离δ，需要找到是否存在距离小于δ的两个点，一个在左边区域，另一个在右边区域。而且这两个点都在距离分界线为δ的区域内。同时可以证明，对于这个区域的每个点，只需考虑后续的7个点即可。具体的思路和证明可以参考《算法导论》第33.4节，这个问题也说明了对于分治法，合并是难点。虽然看上去与最大子序列的形式很像，但是合并操作要复杂得多。同时，最近点对问题在《编程之美》2.11节也出现了，如果没心思去翻《算法导论》，看看《编程之美》上的说明也可以。

延伸：分治法的最坏情况讨论

　　根据合并过程，如果每次的最长子向量都恰好位于边界，即下图中灰色部分，两者其中之一：

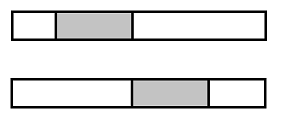
结果导致每次合并时都重复计算了在左边和右边的最长子向量，相当的浪费。解决方法是返回值中给出边界，如果边界在分界点上，合并时就不需要重复计算了。

 

4.扫描算法

　　从头到尾扫描数组，扫描至array[i]时，可能的最长子向量有两种情况：要么在前i-1个元素中，要么以i结尾。前者的大小记为maxsofar，后者记为maxendinghere。

int max_array_v4(int *array,int length) {
    int i;
    int maxsofar = NI;
    int maxendinghere = 0;
    for(i=0;i<length;i++) {
        maxendinghere = maxnum(maxendinghere + array[i],array[i]);
        //分析：maxendinghere必须包含array[i]
        //当maxendinghere>0且array[i]>0，maxendinghere更新为两者和
        //当maxendinghere>0且array[i]<0，maxendinghere更新为两者和
        //当maxendinghere<0且array[i]<0，maxendinghere更新为array[i]
        //当maxendinghere<0且array[i]>0，maxendinghere更新为array[i]
        maxsofar = maxnum(maxsofar,maxendinghere);
    }
    return maxsofar;
}

　　这个算法可以看做是动态规划，把长度为n的数组化成了递归的子结构，并从首开始扫描求解。时间复杂度只有O(n)。

 

附加讨论：

Q：maxsofar的初值不设为一个很大的负数而是0会有什么结果？

A：如果最大子向量为负数，将检测不出来。虽然原书正文中是将初值设为0并在习题8.9给与提醒，但很容易让人迷惑。

 

Q：为什么这些算法在处理int数组时工作的很好，但处理float型时结果不一致？

A：这是由于浮点数的近似，当两个浮点数的差别不大时，是可以认为它们相等的。（习题8.7）

 

相关问题：

1.（习题8.10）查找总和最接近0的连续子序列，尽量用最优方法。进一步地，查找总和最接近某一给定实数t的子向量。

分析：

　　延续对以上几种方法的思路进行讨论。

　　平方方法遍历每对可能的i和j组成的array[i...j]是最直接的，但肯定不是最快。

　　对于分治法，跨越分界点的子序列总要全部遍历一次，但是形式是类似的，虽然使用O(nlongn)能够解决，仍并非最佳。

　　对于扫描算法，如果其他不变，在更新maxendinghere时遇到了困难：在增加array[i]时，如何确定前面的几个连续元素的去留情况？扫描算法无法简单地解决这个问题。

　　这时考虑累加和数组的方法。对于累加和，可以看出如果array[l-1]和array[u]的值越接近，那么array[l...u]就越近0。为了在数组中寻找两个最接近的数，有一个简单方法是排序，用O(n)时间遍历每一对相邻元素。根据这个思路，仅仅需要把累加数组中的结果排序遍历一次，就能获得结果了。但是要注意的是，如果想从排序后的数组中获得原向量的子向量的下标，需要比较大小，较小的是首元，较大的是尾元。

　　另外，考虑一般情况：查找总和最接近某一给定实数t的子向量，我是按照平移的思想来处理的，比如t=25，那么50到t的距离是50-t=25，-50到t的距离是-50-25=-75，把原向量做了一个变化。

#include <stdio.h>
#include <stdlib.h>
#define UT 32768
typedef struct ap ap;
struct ap {
    //array plus
    int key;
    int pos;
};

int comp(const void *ap1,const void *ap2){
    if(((ap*)ap1)->key > ((ap*)ap2)->key)
        return 1;
    else if(((ap*)ap1)->key < ((ap*)ap2)->key)
        return -1;
    else
        return 0;
}

int rabs(int x,int n) {
    if(x>n)
        return x-n;
    else
        return n-x;
}

int most_close_array(int *array,int length,int n){
    int i,j,k;
    int offset = UT;
    int temp;
    ap *realcumarr,*cumarr;
    realcumarr = (ap *)malloc((length+1)*(sizeof(ap)));
    cumarr = realcumarr + 1;
    (cumarr-1)->key = 0;
    (cumarr-1)->pos = -1;
    for(i=0;i<length;i++) {
        (cumarr+i)->key = (cumarr+i-1)->key + array[i] - n;
        //n for shifting to array[i]
        (cumarr+i)->pos = i;
    }
    qsort(cumarr,length,sizeof(ap), comp);
    //cumarr is in increasement order

    for(i=0;i<length;i++)
        printf("i:%d key:%d pos:%d\n",i,(cumarr+i)->key,(cumarr+i)->pos);
    i=j=0;
    for(k=0;k<length-2;k++) {
        //complex fix
        if((cumarr+k+1)->pos > (cumarr+k)->pos) {
            //u = (cumarr+k+1)->pos
            //l-1 = (cumarr+k)->pos
            temp = rabs((cumarr+k+1)->key - (cumarr+k)->key,n);
            if(temp<offset) {
                offset = temp;
                i = (cumarr+k)->pos +1;
                j = (cumarr+k+1)->pos;
            }
        }
        else
        {
            temp = rabs((cumarr+k)->key - (cumarr+k+1)->key,n);
            if(temp<offset) {
                offset = temp;
                i = (cumarr+k+1)->pos +1;
                j = (cumarr+k)->pos;
            }
        }    
    }
    //[l,u] = c[u] - c[l-1] (not c[l])
    printf("[%d,%d]\n",i,j);
    return 0;
}

int main(){
    int n;
    int a[] = {31,-41,59,26,-53,58,97,-93,-23,84};
    printf("please input a base:\n");
    scanf("%d",&n);
    most_close_array(a,sizeof(a)/sizeof(int),n);
    return 0;
}
能解决一般情况下t的完整程序

 

2.（习题8.12）对数组array[0...n-1]初始化为全0后，执行n次运算：for i = [l,u] {x[i] += v;}，其中l,u,v是每次运算的参数，0<=l<=u<=n-1。直接用这个伪码需要O(n2)的时间，请给出更快的算法。

分析：

　　每次运算时取一个子向量进行所有元素相同的操作，那么可以把这个子向量的开始和结尾作为操作的定界，把所有操作叠加起来一次性地完成。

　　即，用下面的代码来代替for i = [l,u] {x[i] += v;}，只使用了O(n)就能完成：

for(...) {//每次迭代
    cum[u]+=v;
    cum[l-1]-=v;
}

for(i=n-1;i>=0;i--)
    x[i] = x[i+1]+cum[i];

 

3.（习题8.14）给定m、n和数组array[n]，请找出使总和array[i...i+m]最接近0的整数i。（0<=i<n-m）

分析：

　　经过上面多次使用累加和数组，这个应该非常简单了。只需要计算出array[0...m]，对一个i，更新sumnew = sumold- array[i-1] +array[i+m]足矣。

 

4.（习题8.13，同样的问题见于《编程之美》2.15）求m*n实数数组的矩形子数组最大和。（即求矩阵最大元素和的子矩阵）

分析：

　　初看这个问题简直无从下手（当然，除了暴力解法），这里的提示是，它和之前的一维数组中的类似问题有什么关系？

　　其实这才是一维数组求最大连续子数组问题的最初形式，当时为了简化分析，Ulf Grenander把二维形式转化为一维，以深入了解其结构。当然这句话看上去并不是那么合理：二维数组压成了一维，少了一维的信息量，怎么反而“深入”了呢？如果这么理解，压缩后只是在一个方向上变化，相当是对问题的抽象，才好理解。

　　有了这个启发，尝试把二维数组压缩了先。可以看出，每个子矩阵都对应一个一维数组，下图的灰色表示把这些元素压缩成了一个，灰色的这一行就是当前处理的子矩阵：

　　同时这个压缩有个好处：当处理的子矩阵在m维度上移动时，可以把灰色部分的元素和直接与新增的元素求和，就得到了新的子矩阵的压缩后的灰色部分。处理灰色的等价一维数组用前面的方式完成，这也是为什么答案提示“在m的维度上使用算法2，在n的维度上使用算法4”。

int MaxSubMatrix(int m[4][4],int row,int col){
    int i,j,k;
    int maxsofar=NI,maxendinghere;
    int *vec;
    vec = (int*)malloc(sizeof(int)*col);
    for(i=0;i<row;i++) {
        bzero(vec,sizeof(int)*col);
        for(j=i;j<row;j++) {
            maxendinghere = 0;
            for(k=0;k<col;k++) {//合并了
                vec[k] += m[j][k];
                maxendinghere = maxnum(maxendinghere + vec[k],vec[k]);
                maxsofar = maxnum(maxsofar,maxendinghere);
            }
        }
    }
    return maxsofar;
}

　　答案上提到还有更快的算法，不过提升有限，运行时间为O(n3[(loglogn)/(logn)]1/2)，想必很复杂，这里也没有进一步研究的必要了。

　　

　　到本文为止，“珠玑之椟”系列就结束了，我已经对《编程珠玑》上的算法和相关的引申问题做了一个分析和介绍，希望读者能有所收获，也希望能作为便于速查的资料。后续和算法相关的博文不再使用这个前缀。

 

 

往期回顾：

     “珠玑之椟”系列简介与索引

　　位向量/位图的定义和应用

　　估算的应用与Little定律

　　随机数函数取样与概率

　　浅谈代码正确性：循环不变式、断言、debug

　　二分思想与分治法、排序思想

posted @ 2013-07-08 20:46  五岳  阅读(7065)  评论(4)  编辑  收藏  举报
回到顶部