codeforces 809C Find a car

codeforces 809C Find a car

题意

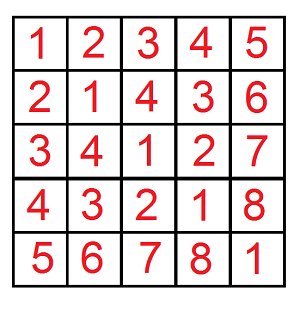
有个\(1e9*1e9\)的矩阵，行 \(x\) 从上到下递增，列 \(y\) 从左到右递增。每个格子有一个正值。\((x, y)\) 的值为 \((i, y)、(x, j) (1<=i<x, 1<=j<y)\) 中没有出现过的最小正整数。
\(1e4\)次询问，每次询问一个子矩阵中值小于等于\(k\)的数之和。

题解

1、\(val(x, y) = (x-1) XOR (y-1) + 1\)
类比尼姆博弈可证。

2、非递归形式的数位dp。\(cnt[p][i][j][k]、sum[p][i][j][k]\)。

代码

#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define rep(i, a, b) for(int i=(a); i<(b); i++)
#define sz(x) (int)x.size()
#define de(x) cout<< #x<<" = "<<x<<endl
#define dd(x) cout<< #x<<" = "<<x<<" "
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;
//------

const int mod=1e9+7, N=33;

ll sum[N][2][2][2], cnt[N][2][2][2];

void upd(ll &a,ll b) {
	a=(a+b)%mod;
	if(a<0) a+=mod;
}

ll solve(int x,int y,int n) {
	if(x<0||y<0) return 0;
	vi dx, dy, dn;
	rep(i,0,N) {
		dx.pb(x&1);
		dy.pb(y&1);
		dn.pb(n&1);
		x>>=1;y>>=1;n>>=1;
	}
	reverse(dx.begin(), dx.end());
	reverse(dy.begin(), dy.end());
	reverse(dn.begin(), dn.end());
	memset(sum,-1,sizeof(sum));
	memset(cnt,-1,sizeof(cnt));
	sum[0][1][1][1]=0;
	cnt[0][1][1][1]=1;
	rep(p,0,N-1) {
		rep(i,0,2) rep(j,0,2) rep(k,0,2) if(~cnt[p][i][j][k]) {
			rep(x,0,2) {
				if(i&&(x>dx[p+1])) continue;
				rep(y,0,2) {
					if(j&&(y>dy[p+1])) continue;
					int z=(x^y);
					if(k&&(z>dn[p+1])) continue;
					ll &_ = cnt[p+1][i&&(x==dx[p+1])][j&&(y==dy[p+1])][k&&(z==dn[p+1])];
					ll &c = sum[p+1][i&&(x==dx[p+1])][j&&(y==dy[p+1])][k&&(z==dn[p+1])];
					if(_==-1) _=0;
					if(c==-1) c=0;
					upd(_, cnt[p][i][j][k]);
					upd(c, sum[p][i][j][k]);
					upd(c, z*(1ll<<(N-1-p-1))*cnt[p][i][j][k]);
				}
			}
		}
	}
	ll a1=0, a2=0;
	rep(i,0,2) rep(j,0,2) rep(k,0,2) if(~cnt[N-1][i][j][k]) {
		upd(a1, cnt[N-1][i][j][k]);
		upd(a2, sum[N-1][i][j][k]);
	}
	return (a1+a2)%mod;
}

int main() {
	int T;scanf("%d",&T);
	while(T--) {
		int a,b,c,d,n;
		scanf("%d%d%d%d%d",&a,&b,&c,&d,&n);
		--a;--b;--c;--d;--n;
		ll ans=0;
		upd(ans,solve(c,d,n));
		upd(ans,solve(a-1,b-1,n));
		upd(ans,-solve(a-1,d,n));
		upd(ans,-solve(c,b-1,n));
		printf("%lld\n",ans);
	}
	return 0;
}