FFT算法实现——基于GPU的基2快速傅里叶变换
最近做一个东西,要用到快速傅里叶变换,抱着蛋疼的心态,自己尝试写了一下,遇到一些问题。
首先看一下什么叫做快速傅里叶变换(FFT)(来自Wiki):
快速傅里叶变换(英语:Fast Fourier Transform, FFT),是离散傅里叶变换的快速算法,也可用于计算离散傅里叶变换的逆变换。快速傅里叶变换有广泛的应用,如数字信号处理、计算大整数乘法、求解偏微分方程等等。
对于复数串行 ,离散傅里叶变换公式为:
,离散傅里叶变换公式为:
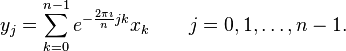
直接变换的计算复杂度是O(n^2).快速傅里叶变换可以计算出与直接计算相同的结果,但只需要O(nlogn)的计算复杂度。
参考:快速傅里叶变换Wiki
首先,看一个概念叫做N次单位复根:复数WN^n = 1。N次单位复根一共有N个,分别为:W(k,N) = cis(2*PI*k/N),k=0,1,...,n-1
其中cis(u) = e^i*u = cos(u) + isin(u)(欧拉公式)
参考:欧拉公式Wiki
N次单位复根有如下性质:
- W(k+N,N) = W(k,N)
- W(k+N/2,N) = -W(k,N)
- W(dk,dN) = W(k,N) (d>0)
库利-图基算法:
将长度为N的序列分成两个N/2的子序列N1和N2,其中N1是原来序列的奇数项,N2为偶数项。
将离散傅里叶变换写成:
N(x) = ∑(j=0,n-1)aj*xj x = W(k,N)
分解后有:
N1(x) = a0 + a2*x + a4*x^2 + ... + a(n-2)*x^(n/2-1)……1
N2(x) = a1 + a3*x + a5*x^2 + ... + a(n-1)*x^(n/2-1)……2
N(x) = N1(x^2) + x*N2(x^2)……3
就这样将(W(0,N))^2,(W(1,N))^2,...,(W(N-1,N))^2一个一个往1,2式代,然后根据3式组合就可以得到结果了。
按照相同的办法,将此式递归下去,最终就可以得到结果。这就是库利-图基算法的大概思想。
语言描述起来很抽象,使用蝴蝶网络来表示,就可以一目了然:
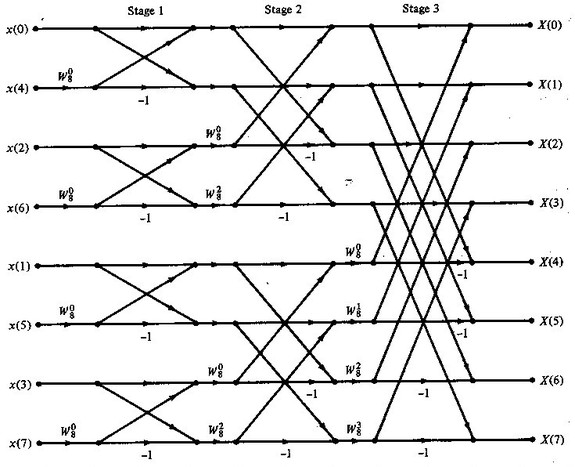
如图,展示了一个N=8的快速傅里叶变换执行流程。
按照这种算法,可以很快写出递归算法类C伪代码:
Array recursive_fft(a) { int n = a.lengh(); if(n=1) return a; W wn = e^2*PI*i/n; W w = 1; Array a0 = {a0,a2,a3……a(n-2)}; Array a1 = {a1,a3,a5……a(n-1)}; Array y0 = recursive(a[0]); Array y1 = recursive(a[1]); Array y; for(int k = 0;k<=n/2-1;++k) { y[k] = y0[k]+wy1[k]; y[k+n/2] = y0[k]-wy1[0]; w *= wn } return y; }
然而,FFT在实际应用中往往需求很高的效率,虽然都是O(n*logn)d的时间复杂度,但是在递归的实现算法中,隐含的常数更大(这点可以参考《算法导论》的相关内容,这里不做具体讨论)。并且,递归的方案也不好用GPU实现。
所以需要实现迭代的FFT,参考算法导论相代码实现如下:
#pragma once #include "RBVector2" class RBFFTTools { public: static void iterative_fft(RBVector2 *v,RBVector2 *out,int len) { bit_reverse_copy(v,out,len); int n = len; for (int s = 1; s <= log(n)/log(2);s++) { int m = pow(2, s); RBVector2 wm(cos(2 * PI / m), sin(2 * PI / m)); for (int k = 0; k < n ;k+=m) { RBVector2 w = RBVector2(1,0); for (int j = 0; j < m / 2;++j) { RBVector2 vv = out[k + j + m / 2]; RBVector2 t = RBVector2(w.x*vv.x - w.y*vv.y,w.x*vv.y+w.y*vv.x); RBVector2 u = out[k + j]; out[k + j] = RBVector2(u.x+t.x,u.y+t.y); out[k + j + m / 2] = RBVector2(u.x-t.x,u.y-t.y); w = RBVector2(w.x*wm.x - w.y*wm.y, w.x*wm.y + w.y*wm.x); } } } } //逆变换 static void iterative_ifft(RBVector2 *v, RBVector2 *out, int len) { bit_reverse_copy(v, out, len); int n = len; for (int s = 1; s <= log(n)/log(2); s++) { int m = pow(2, s); RBVector2 wm(cos(2 * PI / m), sin(2 * PI / m)); for (int k = 0; k < n; k += m) { RBVector2 w = RBVector2(1, 0); for (int j = 0; j < m / 2; ++j) { RBVector2 vv = out[k + j + m / 2]; RBVector2 t = RBVector2(w.x*vv.x - w.y*vv.y, w.x*vv.y + w.y*vv.x); RBVector2 u = out[k + j]; out[k + j] = RBVector2(u.x + t.x, u.y + t.y); out[k + j + m / 2] = RBVector2(u.x - t.x, u.y - t.y); w = RBVector2(w.x*wm.x + w.y*wm.y, -w.x*wm.y + w.y*wm.x); } } } for (int i = 0; i < n;++i) { out[i].x /= n; out[i].y /= n; } } private: static void bit_reverse_copy(RBVector2 src[], RBVector2 des[], int len) { for (int i = 0; i < len;i++) { des[bit_rev(i, len-1)] = src[i]; } } public: static unsigned int bit_rev(unsigned int v, unsigned int maxv) { unsigned int t = log(maxv + 1)/log(2); unsigned int ret = 0; unsigned int s = 0x80000000>>(31); for (unsigned int i = 0; i < t; ++i) { unsigned int r = v&(s << i); ret |= (r << (t-i-1)) >> (i); } return ret; } };
上面的代码出现了两个函数:bit_reverse_copy()和bit_rev(),这两个函数用于将初始数据按照bit反转顺序进行排序。
bit反转看下面例子就可了然:
| 000 | 000 |
| 001 | 100 |
| 010 | 010 |
| 011 | 110 |
| 100 | 001 |
| 101 | 101 |
| 110 | 011 |
| 111 | 111 |
即把所有bit位冲头到尾颠倒一次。
上面iterative_ifft()是逆变换,逆变换很简单就可以修改出来,只需要根据W的性质进行修改W的更新,以及除以一个N就可以了。
运行结果如下:
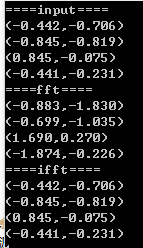
参考:算法导论 第30章
基于GPU的FFT
这里使用OpenGL的Fragment Shader来实现FFT,我使用了两个浮点纹理作为输入,一个纹理表示蝴蝶网络,一个表示当前的输入数据:
一个N(2的幂)的FFT需要迭代log_2(N)次,蝴蝶网络和输入数据每次迭代都会更新,更新的数据用于下次迭代输入,输出的数据使用FBO来暂存,效率还可以。
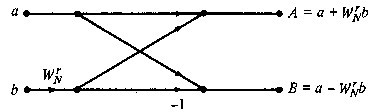
蝴蝶网络的单元结构如下:

输入数据仅用了四个通道中的前两个,用来存放数据的实部和虚部。
GPU算法可以通过蝴蝶网络图很容易的得出:

观察此图,可以发现:
每次迭代都需要输出数据,输出的数据由下图计算方案决定:

W(r,N)就储存在对应的蝴蝶网络纹理中,取出来就可以了。
另外,每次迭代后都要对于蝴蝶网络更新,更新的内容包括:
更新W和更新对应项的索引x,y值,由上图可以知道,W只需下标乘以2得到Nnew,上标依次从零到Nnew,以此2循环即可。因为转换一下就可以知道,W的变换其实是下面这个规律:
W(0,2) W(0,4) W(0,8) W(0,16) ……
W(1,2) W(1,4) W(1,8) W(1,16) ……
W(2,4) W(2,8) W(2,16) ……
W(3,4) W(3,8) W(3,16) ……
W(4,8) W(4,16) ……
W(5,8) .................
W(6,8) .................
W(7,8) .................
.................
而索引的变换就更加简单了,加上当前的迭代次数即可。
思路很简单,但是调试的时候很蛋疼,给出的代码使用了OpenFrameworks提供的OpenGL框架:
#include "ofApp.h" #include "time.h" time_t t_s1,t_e1; time_t t1,t2; void ofApp::setup() { ofDisableArbTex(); imag_test.loadImage("1.jpg"); first = true; N = 1024; cur = 0; source = new RBVector2[N*N]; rev_source = new RBVector2[N*N]; out = new RBVector2[N*N]; //禁用Alpha混合,否则绘制到FBO会混合Alpha,造成数据丢失 ofDisableAlphaBlending(); for(int i=0;i<2;i++) { weight_index[i].allocate(N,N,GL_RGBA32F); res_back[i].allocate(N,N,GL_RGBA32F); data[i].allocate(N,N,ofImageType::OF_IMAGE_COLOR_ALPHA); } //初始化蝴蝶网络 for(int i=0;i<N;i++) { for(int j=0;j<N;j++) { if(j%2==0) data[0].setColor(j,i,ofFloatColor(0.f,2.f,(float)((i*N+j+1)%N),(float)((i*N+j+1)/N))); else data[0].setColor(j,i,ofFloatColor(1.f,2.f,(float)((i*N+j-1)%N),(float)((i*N+j-1)/N))); } } //初始化原始数据,这里使用随机数 for(int i=0;i<N*N;i++) { float s1 = ofRandomf(); float s2 = ofRandomf(); source[i] = RBVector2(s1,s2); } t_s1 = time(0); bit_reverse_copy(source,rev_source,N*N); t_e1= time(0); t2 = t_e1 - t_s1; //初始化到纹理数据 for(int i=0;i<N;i++) { for(int j=0;j<N;j++) { data[1].setColor(j,i,ofFloatColor(rev_source[i*N+j].x,rev_source[i*N+j].y,0,1)); } } data[0].update(); data[1].update(); weight_index[0].begin(); data[0].draw(0,0,N,N); weight_index[0].end(); res_back[0].begin(); data[1].draw(0,0,N,N); res_back[0].end(); ofSetWindowShape(1280,720); weight_index_shader.load("normalv.c","generate_weight_and_index_f.c"); gpu_fft_shader.load("normalv.c","gpu_fft_f.c"); t_s1 = time(0); //CPU变换 RBFFTTools::iterative_fft(source,out,N*N); t_e1 = time(0); t1 = t_e1 - t_s1; } //-------------------------------------------------------------- void ofApp::draw() { if(first) { t_s1 = time(0); for(int i = 1;i<N*N;i*=2) { res_back[1-cur%2].begin(); //更新输出 gpu_fft_shader.begin(); gpu_fft_shader.setUniform1i("size",N); gpu_fft_shader.setUniform1i("n_step",i); gpu_fft_shader.setUniform3f("iResolution",N,N,0); gpu_fft_shader.setUniformTexture("tex_index_weight",weight_index[cur].getTextureReference(),1); gpu_fft_shader.setUniformTexture("tex_res_back",res_back[cur].getTextureReference(),2); gpu_fft_shader.setUniformTexture("test",imag_test.getTextureReference(),4); ofRect(0,0,N,N); gpu_fft_shader.end(); res_back[1-cur%2].end(); //更新蝴蝶网络数据 weight_index[1-cur%2].begin(); weight_index_shader.begin(); weight_index_shader.setUniform1i("size",N); weight_index_shader.setUniform1i("n_step",i); weight_index_shader.setUniform3f("iResolution",N,N,0); weight_index_shader.setUniformTexture("tex_input",weight_index[cur].getTextureReference(),1); ofRect(0,0,N,N); weight_index_shader.end(); weight_index[1-cur%2].end(); cur = 1 - cur%2; } t_e1= time(0); t2 += (t_e1 - t_s1); cout<<"==================↓gpu================"<<endl; //输出GPU计算结果 for(int i=0;i<N;i++) { for(int j=0;j<N;j++) { //cout<<s.getColor(j,i).r<<","<<s.getColor(j,i).g<<endl; } } cout<<"==================↓cpu================"<<endl; //输出CPU计算结果 for(int i=0;i<N;i++) { for(int j=0;j<N;j++) { int index = i*N+j; //cout<<out[index].x<<","<<out[index].y<<endl; } } cout<<"===================================="<<endl; //对比CPU和GPU计算结果 for(int i=0;i<N;i++) { for(int j=0;j<N;j++) { float rx = s.getColor(j,i).r; float ry = s.getColor(j,i).g; int index = i*N+j; float delta = 0.1; if(abs(rx-out[index].x)>delta||abs(ry-out[index].y)>delta) { //数据在误差范围外,出错 goto wrong; //cout<<s.getColor(j,i).r<<","<<s.getColor(j,i).g<<"|"<<out[index].x<<","<<out[index].y<<endl; } else { //cout<<s.getColor(j,i).r<<","<<s.getColor(j,i).g<<","<<s.getColor(j,i).b<<","<<s.getColor(j,i).a<<endl; } } } cout<<"CPU:"<<t1<<endl<<"GPU:"<<t2<<endl; first = !first; } if(false) { wrong: printf("wrong!!!\n"); } //绘制数据输入纹理和数据输出纹理 res_back[cur].draw(N,0,N,N); data[1].draw(0,0,N,N); }
更新数据Shader:
#version 130 uniform sampler2D tex_index_weight; uniform sampler2D tex_res_back; uniform sampler2D test; uniform int size; uniform int n_step; uniform vec3 iResolution; out vec4 outColor; void main() { vec2 tex_coord = gl_FragCoord.xy/iResolution.xy; float cur_x = gl_FragCoord.x - 0.5; float cur_y = gl_FragCoord.y - 0.5; vec2 outv; vec4 temp = texture(tex_index_weight,tex_coord); vec2 weight = vec2(cos(temp.r/temp.g*2*3.141592653),sin(temp.r/temp.g*2*3.141592653)); vec2 _param2_index = temp.ba; vec2 temp_param2_index = _param2_index; temp_param2_index.x += 0.5; temp_param2_index.y += 0.5; vec2 param2_index = temp_param2_index/iResolution.xy; vec2 param1 = texture(tex_res_back,tex_coord).rg; vec2 param2 = texture(tex_res_back,param2_index).rg; int tex_coord_n1 = int((cur_y*size)+cur_x); int tex_coord_n2 = int((_param2_index.y*size)+_param2_index.x); if(tex_coord_n1<tex_coord_n2) { outv.r = param1.r + param2.r*weight.r-weight.g*param2.g; outv.g = param1.g +weight.r*param2.g + weight.g*param2.r; } else { outv.r = param2.r + param1.r*weight.r-weight.g*param1.g; outv.g = param2.g +weight.r*param1.g + weight.g*param1.r; } outColor = vec4(outv,0,1); }
更新蝴蝶网络Shader:
#version 130 uniform sampler2D tex_input; uniform int size; uniform int n_total; uniform int n_step; in vec3 normal; uniform vec3 iResolution; out vec4 outColor; void main() { vec2 tex_coord = gl_FragCoord.xy/iResolution.xy; float cur_x = gl_FragCoord.x - 0.5; float cur_y = gl_FragCoord.y - 0.5; vec4 outv; int tex_coord_n = int((cur_y*size)+cur_x); //updata weight vec2 pre_w = texture(tex_input,tex_coord).rg; float i = pre_w.r; float n = pre_w.g; float new_i; float new_n; new_i = i; new_n = n*2; if(tex_coord_n%(n_step*4) > n_step*2-1) { new_i += n_step*2; } outv.r = new_i; outv.g = new_n; //updata index vec2 pre_index = texture(tex_input,tex_coord).ba; int x = int(pre_index.x); int y = int(pre_index.y); int ni = n_step*2; int new_tex_coord_n = tex_coord_n; if((tex_coord_n/ni)%2==0) { new_tex_coord_n += ni; } else { new_tex_coord_n -= ni; } outv.b = new_tex_coord_n%size; outv.a = new_tex_coord_n/size; outColor = outv; }
用time大概对比了一下GPU和CPU的计算时间,结果如下:

N = 512*512的情况下,误差在0.1以内,在我的应用情况下是可以接受的,更高的数据意味着更多的迭代次数,会进一步降低数据精度,目前还没有解决误差问题。
运行50次,大概对比如下,不是很准确,仅供参考:






