数据结构-树的那些事(四)
一、树
树是一种类似于链表的数据结构,链表是以线性的方式简单地指向其后端地节点,而树的一个节点可以指向许多个节点,树是一种典型的非线性结构。树是一种表达具有层次特征的图结构的一种方法。
二、树的基本术语
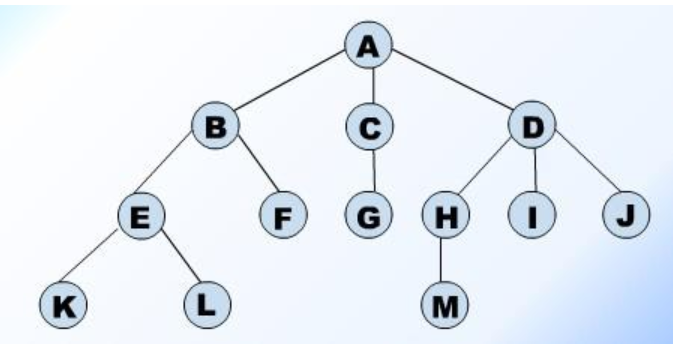
上图是一张树的结构,针对这张图我们来理解下树的基本术语;
根节点:其中的A点就是树跟结点,A点的特征就是没有双亲结点,另外一个点就是一棵树只有一个根结点;
叶子结点:其中K,L,F,G,M,I,J是叶子节点,没有孩子的结点就是叶子结点;
兄弟结点:拥有共同的双亲结点的孩子结点就是叶子结点,其中B,C,D是A的兄弟结点;
结点的大小:结点的大小是子孙的个数包括自身结点,其中C的大小为2;
树的层:位于相同深度的所层叫做树的层,上图就是3层树,层是从0开始计算的;
树的高度:树中所有结点高度的最大值,树的深度所有结点深度的最大值,一棵树深度和高度是相同的,但是针对于子节点来说不一定相同的;
斜树:每个结点自有一个孩子结点的树叫做斜树,只有左孩子结点的叫做左斜树,同理叫做右斜树;
三、理解下树的结构问题
在这之前我们讨论过顺序存储和链表存储的结构,这里我们借助于二叉树来讨论下树的存储结构,
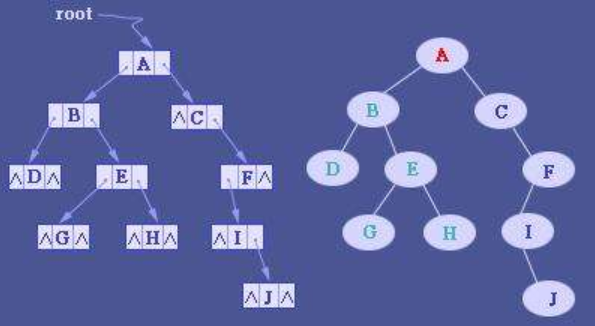
上图就是二叉树,我左边已经给出最好的数据结构类型,不够还是要来说下为什么不用顺序存储二叉树,现在假设A左子树是不存在的,按照顺序存储该二叉树的话我们需要2的5次方减去1才能将这二叉树完整的还原,在空间上就有了很大的浪费,所以我们选择链表的结构来存储二叉树,例如左图,还是同样的假设A的左子树只是指向一个空结点就够了,在空间基本没有浪费,就可以将完整的二叉树还原;
四、谈一下二叉树
上面我们已经引入二叉树的概念,什么是二叉树?如果一棵树每个结点最多拥有2个孩子结点,那么这个树就是二叉树,就算只有根节点也是满足二叉树的;
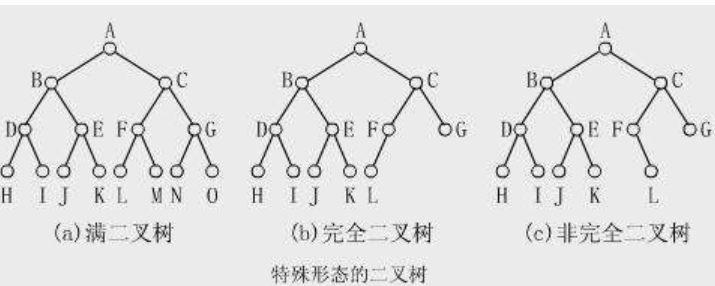
上图是几种不同的二叉树,根据子节点的不同可以分成以上几种不同的二叉树,这里解释一下完全二叉树,如果所有的孩子结点深度为h或者h-1,并且结点的编号没有漏调任数字,就叫做完全二叉树,这里还要引入一个严格二叉树的概念,每个结点要么有2个孩子结点,要么没有孩子结点,来几句绕的话,满二叉树一定是完全二叉树,也一定是严格二叉树,完全二叉树不一定是严格二叉树;
接下来我们谈一下二叉树的遍历,根据结点处理顺序的不同我们分为3种遍历的方法:
前序遍历:根左右
中序遍历:左根右
后序遍历:左右根
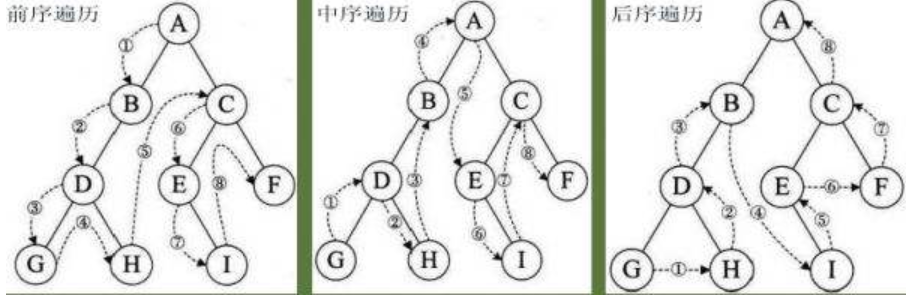
一看图就明白了,这里我想说下在实现3中遍历的时候我使用了递归和非递归的方法,先说下递归和迭代个各自的优缺点:
递归
1)当满足条件时候,递归终址;
2)每次调用递归都需要额外的空间用于内存的开销;
3)如果出现无穷递归程序会内存耗尽,导致栈溢出;
4)有些情况使用递归可以更容易解决;
迭代
1)当满足条件的时候,迭代终止;
2)每次迭代不需要额外的空间开销;
3)一旦出现死循环由于没有额外的空间开销,程序不会报错但会一直循环执行;
4)有些情况可能使用迭代的时候代码不好写;
基本情况介绍到这里希望大家循环和迭代的时候考虑好,还需说明一下我使用非递归进行遍历的时候的一些想法和思路,在进行前序和中序遍历借助栈的先进后出的特点进行遍历的,后序遍历稍显不一样使用的是两个栈进行的遍历;
前序:
首先遍历根节点,然后将右子树压栈,最后将左子树压栈,因为后进先出所以首先出栈的是左子树;
中序:
首先将根结点和左子树进行压栈,然后出栈,在出栈的同时将右子树进行压栈;
后序:
首先定义两个栈,一个用于输出显示,另外一个用于保存过渡,声明以后按照根左右的顺序依次将结点进行压栈,导致保存过渡的出栈顺序成为右左根,然而在进行循环保存过渡栈的时候,会进行对输出栈进行压栈,所以就导致输出栈入栈的顺序是根右左,出栈的时候是左右根;
以上是非递归遍历的时候注意点,另外我还使用了一种层次遍历,是借助于队列的特征,按照根左右的特点进行入队,最后就根左右的顺序出队,下面上代码;
结点的定义:

/** * Created by wangt on 2017/8/1. * 树节点的定义 */ public class Node<T> { public T getData() { return data; } public void setData(T data) { this.data = data; } public Node<T> getLchild() { return lchild; } public void setLchild(Node<T> lchild) { this.lchild = lchild; } public Node<T> getRchilid() { return rchilid; } public void setRchilid(Node<T> rchilid) { this.rchilid = rchilid; } //数据 private T data; //左子树 private Node<T> lchild; //右子树 private Node<T> rchilid; public Node(T data) { this.data=data; } public Node(T data,Node<T> lchild,Node<T> rchilid) { this.data=data; this.lchild=lchild; this.rchilid=rchilid; } }
二叉树的遍历以及基本操作

public class BinaryTree<T> { public Node<T> getRoot() { return root; } private Node<T> root; public BinaryTree(T data) { this.root=new Node<T>(data); } /* 判断是否为空 */ public boolean isEmpty() { return this.root==null; } /* 在某P节点左子树下插入data */ public void insertLeft(Node<T> p,T data) { Node<T> tempNode=new Node<T>(data); tempNode.setLchild(p.getLchild()); p.setLchild(tempNode); } /* 在某P节点右子树下插入data */ public void insertRight(Node<T> p,T data) { Node<T> tempNode=new Node<T>(data); tempNode.setRchilid(p.getRchilid()); p.setRchilid(tempNode); } /* 删除左子树 */ public Node<T> removeLeft(Node<T> p) { if(p==null||p.getLchild()==null) { return null; } Node<T> tempNode=p.getLchild(); p.setLchild(null); return tempNode; } /* 删除右子树 */ public Node<T> removeRight(Node<T> p) { if (p==null||p.getRchilid()==null) { return null; } Node<T> tempNode=p.getRchilid(); p.setRchilid(null); return tempNode; } /* 下面3个方法是递归遍历得前 中 后 遍历 */ public void preOrder(Node<T> node) { if(node!=null) { // 根->左->右 System.out.print(node.getData()+" "); preOrder(node.getLchild()); preOrder(node.getRchilid()); } } public void midOrder(Node<T> node) { if(node!=null) { // 左->根->右 midOrder(node.getLchild()); System.out.print(node.getData()+" "); midOrder(node.getRchilid()); } } public void postOrder(Node<T> node) { if (node != null) { // 左->右->根 postOrder(node.getLchild()); postOrder(node.getRchilid()); System.out.print(node.getData() + " "); } } /* 下面3个方法是非递归遍历 */ //前序 public void preOrderNoRecurise(Node<T> node) { if(node==null) { return; } Stack<Node<T>> stack=new Stack<Node<T>>(); stack.push(node); Node<T> tempNode=null; while (stack.size()>0) { //利用stack后进先出得特点进行前序遍历 tempNode=stack.pop(); System.out.print(tempNode.getData()); if (tempNode.getRchilid()!=null) { stack.push(node.getLchild()); } if (tempNode.getLchild()!=null) { stack.push(node.getLchild()); } } } //中序 public void midOrderNoRecurise(Node<T> node) { if (node==null) { return; } Stack<Node<T>> stack=new Stack<Node<T>>(); Node<T> tempNode=node; while (stack.size()>0||tempNode!=null) { //先将左子树压栈 while (tempNode!=null) { stack.push(tempNode); tempNode=tempNode.getLchild(); } //左子树出栈 tempNode=stack.pop(); //跟 System.out.print(tempNode.getData()); //右 tempNode=tempNode.getRchilid(); } } //后序遍历 public void postOrderNoRecurise(Node<T> node) { if (node==null) { return; } //定义2个栈一个出栈一个入栈 Stack<Node<T>> stackIn=new Stack<Node<T>>(); Stack<Node<T>> stackOut=new Stack<Node<T>>(); Node<T> currentNode =null; //跟先压栈 stackIn.push(node); while (stackIn.size()>0) { currentNode=stackIn.pop(); stackOut.push(currentNode); //左子树压栈 while (currentNode.getLchild()!=null) { stackIn.push(currentNode.getLchild()); } //右子树压栈 while (currentNode.getRchilid()!=null) { stackIn.push(currentNode.getRchilid()); } } while (stackOut.size()>0) { Node<T> outNode=stackOut.pop(); System.out.print(outNode.getData()); } } //层次遍历 public void levelOrder(Node<T> node) { if (node==null) { return; } LinkedList<Node<T>> queue=new LinkedList<Node<T>>(); queue.offer(node); Node<T> tempNode=null; while (queue.size()>0) { tempNode=queue.poll(); System.out.print(tempNode.getData()); if (tempNode.getLchild()!=null) { queue.offer(tempNode.getLchild()); } if (tempNode.getRchilid()!=null) { queue.offer(tempNode.getRchilid()); } } } }
测试代码:

public class BinaryTest { public static void main(String[] args) { BinaryTree<String> binaryTree=new BinaryTree<String>("A"); Node<String> rootNode=binaryTree.getRoot(); binaryTree.insertLeft(rootNode,"B"); binaryTree.insertRight(rootNode,"C"); Node<String> nodeB=rootNode.getLchild(); binaryTree.insertLeft(nodeB,"D"); binaryTree.insertRight(nodeB,"E"); Node<String> nodeC=rootNode.getRchilid(); binaryTree.insertRight(nodeC,"F"); binaryTree.levelOrder(rootNode); binaryTree.midOrder(rootNode); } }
五、暂停数据结构和集合介绍
最近进行了SSH的学习,但是发现由于工作中一直使用C#语言做开发,所以导致会忘记,所以准备做一下Meavn整合SSH系列文章,然后在进行数据结构和集合系列,SSH系列的基本想法就是将基本的1对多,多对多这些关系做一下,还有就是框架整合时候的注意点等等,我这边进行思考下,在下片开头会进行详细介绍,至于题目我想暂定.Net开发玩转Java开发;



