神经网络是如何拟合任意函数的

一个最原始粗暴的拟合任意函数的思路，是将函数切成很多段线性函数，之后用逻辑门控制当x在哪一个区间时，某些逻辑门被激活，对应的线性函数的权重w与偏移量b在逻辑门的包裹下变成非0，计算出y在这一段的输出值。

 

需要推导出拟合函数y=f(x)需要哪些逻辑门，以及如何使用神经网络构建这些逻辑门。

开关函数 s： 当u>0时s(u)=1，否则s(u)=0 。右上标数字代表第几层开关。

 

首先最基础的是大于小于开关门：

${s^{(1)}}(x>0) \ni t{\rm{ = Relu}}({\rm{1 - 1000*Relu}}({\rm{u}}))$

使用Relu激活函数构建的开关门比起使用sigmoid函数构建的开关门

 ${s^{(1)}}(x>0) \ni t={\rm{\sigma (1000x)}}$

的作用是相同的，都是让x>0时t=1，否则t=0

通过平移技巧：f(x-p)等价于f(x)平移+p距离，可以指定门的位置。

 

接下来是将开关门进行与/或组合，得到的门。

假如t1负责激活x>6， t3负责激活x>9，那么定义${s^{(2)}}({s^{(1)}}(x)) \ni$ t2 = (t1 and (not t3)) =  $s( t1 - t3)$ ，即可用t2描述 6<x<=9的区间。 

类似的，也可以定义 ${s^{(2)}}({s^{(1)}}(x)) \ni$ t4 = ((not t1) or t3) = $s( - t1 + t3 + 1)$ ，即可用t4描述 x<6 or x>=9 的区间。

 

 

调用上一层的逻辑组合，即可获得更复杂表达的门，例如XOR门：

((not t1) and t3) or (t1 and (not t3))  描述的实数区间其实并不存在

但如果可供描述的区间增多，是允许描述  (6<x<=9) or (14 < x < =17) 这样的区间的。

 

可以看出随着逻辑层数的增加，是允许用一个开关来描述任意复杂的输入区间的。既当x落在该输入区间（partition）内的时候，描述它的开关门的值为1，否则为0。

用个人习惯的描述方式来讲，就是通过逻辑门组合出的能够激活某个神经元的区间，叫做该神经元的激活响应区域（partition）。

 

这里使用了神经网络以及Relu函数构建了一个基础大于/小于门。上述描述的所有门都可以通过类似的方法构建。

 

 既然已经构建了描述区间的门，那么就可以开始拟合函数了。

考虑任意函数，都可以被近似为多段线性函数。简便起见，假设三段线性函数的两个分割点是x=6以及x=9

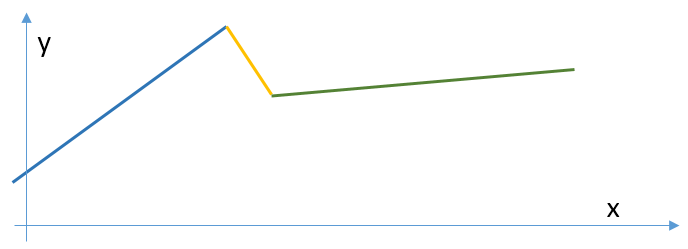
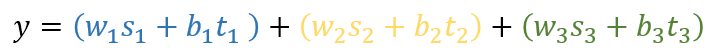
b是偏移量，t是激活门，当x落在对应分段区间i内，激活门  t_i=1，否则t_i = 0

y的值可以分拆成ws的值与bt的值。下面画出了bt与s的值。

 

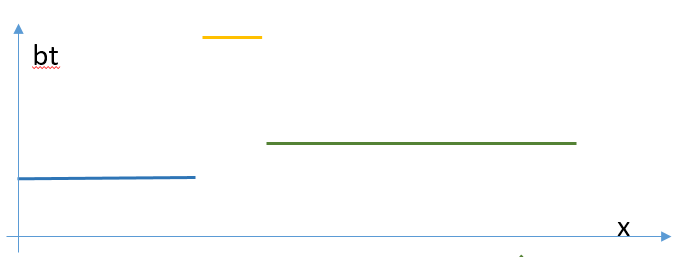
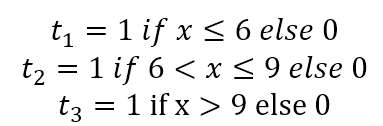
只使用“门”结构t 乘以偏移量毕竟只能用水平线来拟合函数，虽然理论上已经可以近似出所有函数了，但是并不够优雅。

 

这时候可以让“坡”结构s登场了，既平移过后的Relu函数。

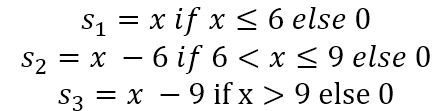
这里尝试结合“门”与“坡” ，再添加一些Identity映射，即可完成对任意函数y的近似拟合。

描述y所需的输入区间(partition)越多，需要的神经元数量越多。或是利用复杂逻辑增加网络层数来缩减隐层的节点个数。