Tarjan算法 求 有向图的强连通分量

百度百科 

https://baike.baidu.com/item/tarjan%E7%AE%97%E6%B3%95/10687825?fr=aladdin

参考博文

http://blog.csdn.net/qq_34374664/article/details/77488976

http://blog.csdn.net/mengxiang000000/article/details/51672725

https://www.cnblogs.com/shadowland/p/5872257.html

算法介绍（基于DFS）

了解tarjan算法之前你需要知道：强连通，强连通图，强连通分量。

强 连 通：如果两个顶点可以相互通达，则称两个顶点强连通(strongly connected)。

在一个有向图G里，设两个点a和b, 发现由a有一条路可以走到b，由b又有一条 路可以走到a，我们就叫这两个顶点（a，b）强连通。（注意间接连接也可以）

强连通图：如果有向图G的每两个顶点都强连通，称G是一个强连通图。

强连通分量：在一个有向图G中，有一个子图G2，这个子图G2每2个点都满足强连通，我们就 把这个子图G2叫做强连通分量 。

我们来看一个有向图方便理解：

 

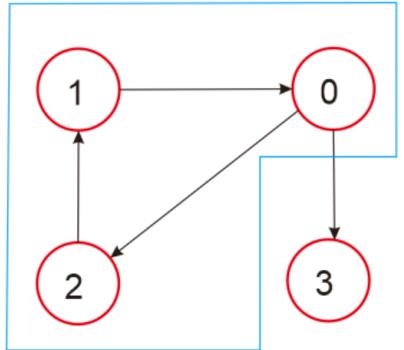
标注蓝色线条框框的部分就是一个强连通分量，节点3也是一个强连通分量

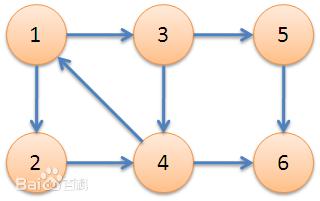
我们再来看一个图（百度百科中的图）：

子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。

 

 

 

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量实际上为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入到一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

 

在Tarjan算法中，有如下定义。

（注意，下面的定义如看不明白没关系，多看后面的模拟就明白了）

DFN[u]数组 : 在DFS中该节点被搜索的次序编号，每个点的次序编号都不一样。

通俗地解释DFN[u]：　意思就是在DFS的过程中，当前的这个节点是第几个被遍历到的点

LOW[u]数组 : u或u的子树能够追溯到的最早的栈中节点的次序号

通俗地解释LOW[u]：　就是在DFS的过程中，如果当前节点是极大强联通子图的话，他的根节点的标号就是对应的LOW值：

 

当DFN[ u ]==LOW[ u ]时，u或u的子树可以构成一个强连通分量。

通俗地解释：当DFN[ u ]==LOW[ u ]时，以u为根的搜索子树上所有节点是一个强连通分量。

 

回溯条件: DFS遇到的节点在已在栈中或者DFS遇到无出度的节点时就回溯。

回溯时需要维护LOW[u]的值。

如果下一个要遍历的节点在栈中，那么就要把当前节点的LOW[u]值设置成下一个节点（在栈中）的DFN[v]值。如：LOW[u]=DFN[v]  或者LOW[u]= min(LOW[u], DFN[v])

如果还需要接着回溯，那么接着维护LOW[u]=min(LOW[u]，LOW[v])

（即使v搜过了也要进行这步操作，但是v一定要在栈内才行）

u代表当前节点，v代表其能到达的节点。在进行一层深搜之后回溯的时候，维护LOW[u]的值。如果我们发现了某个节点回溯之后维护的LOW[u]值还是==DFN[u]的值，那么这个节点无疑就是一个关键节点：

 

算法演示：以1为Tarjan 算法的起始点，如图：前面不明白没关系，重点从这里开始看

 

 

 

假如从1号节点开始遍历，开始dfs，并不断设置当前节点的DFN值和LOW值，并把当前这个节点压入栈中，那么第一次在节点6处停止，因为6没有出度。

那么此时的DFN和LOW值分别为：

从1开始：   DFN［1］＝LOW［1］＝ ＋＋index －－－－1

入栈 1

由1进入3： DFN［3］＝LOW［3］＝ ＋＋index －－－－2

入栈 1  3

由3进入5： DFN［5］＝LOW［5］＝ ＋＋index －－－－3

入栈 1  3  5

由5进入6： DFN［6］＝LOW［6］＝ ＋＋index －－－－4

入栈 1  3  5  6                

可以用下图来表示：

   

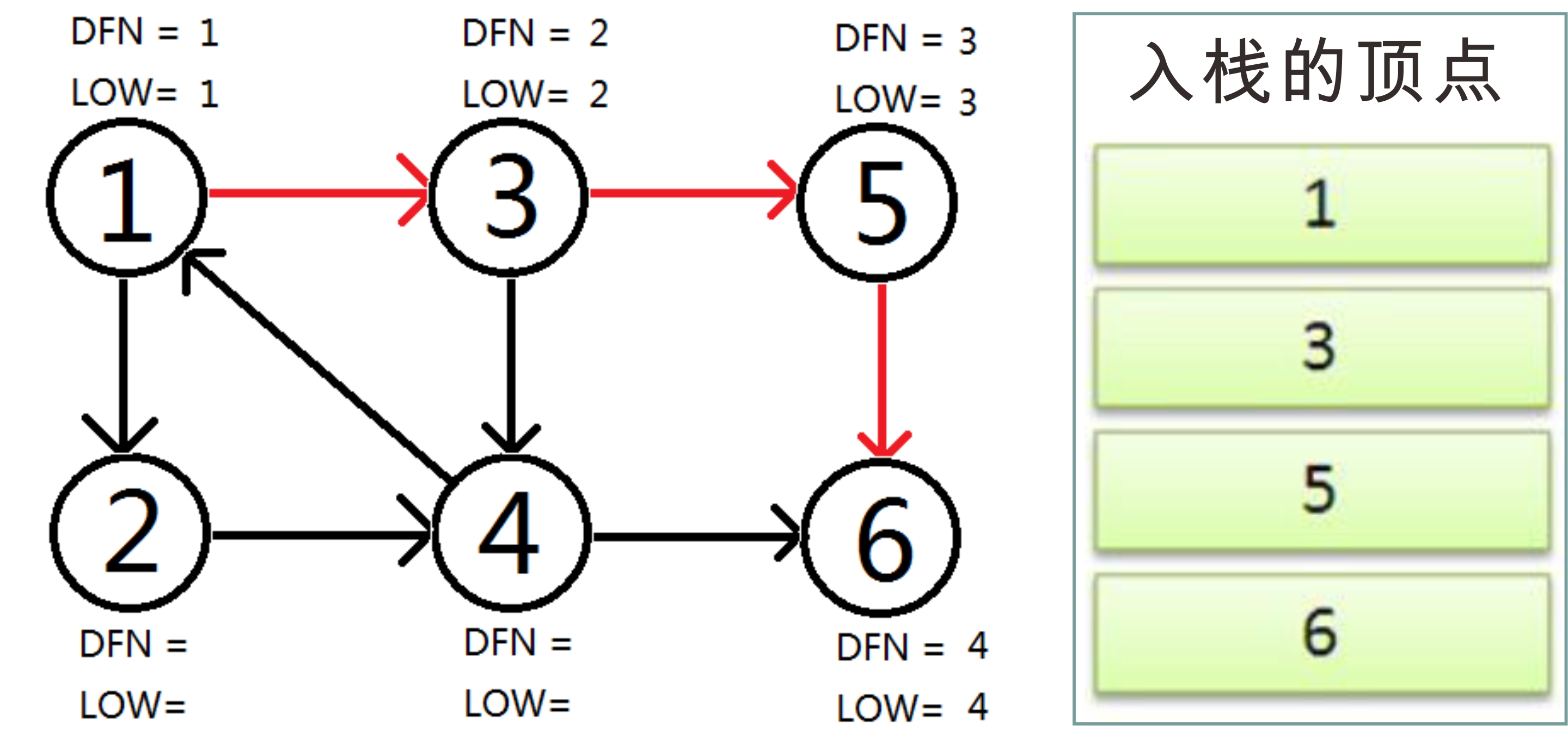
因为节点6无出度，于是判断 DFN［6］＝＝LOW［6］，把6出栈(pop)。

{6}是一个强连通分量。

目前栈的节点有： 1  3  5  见下图：

 

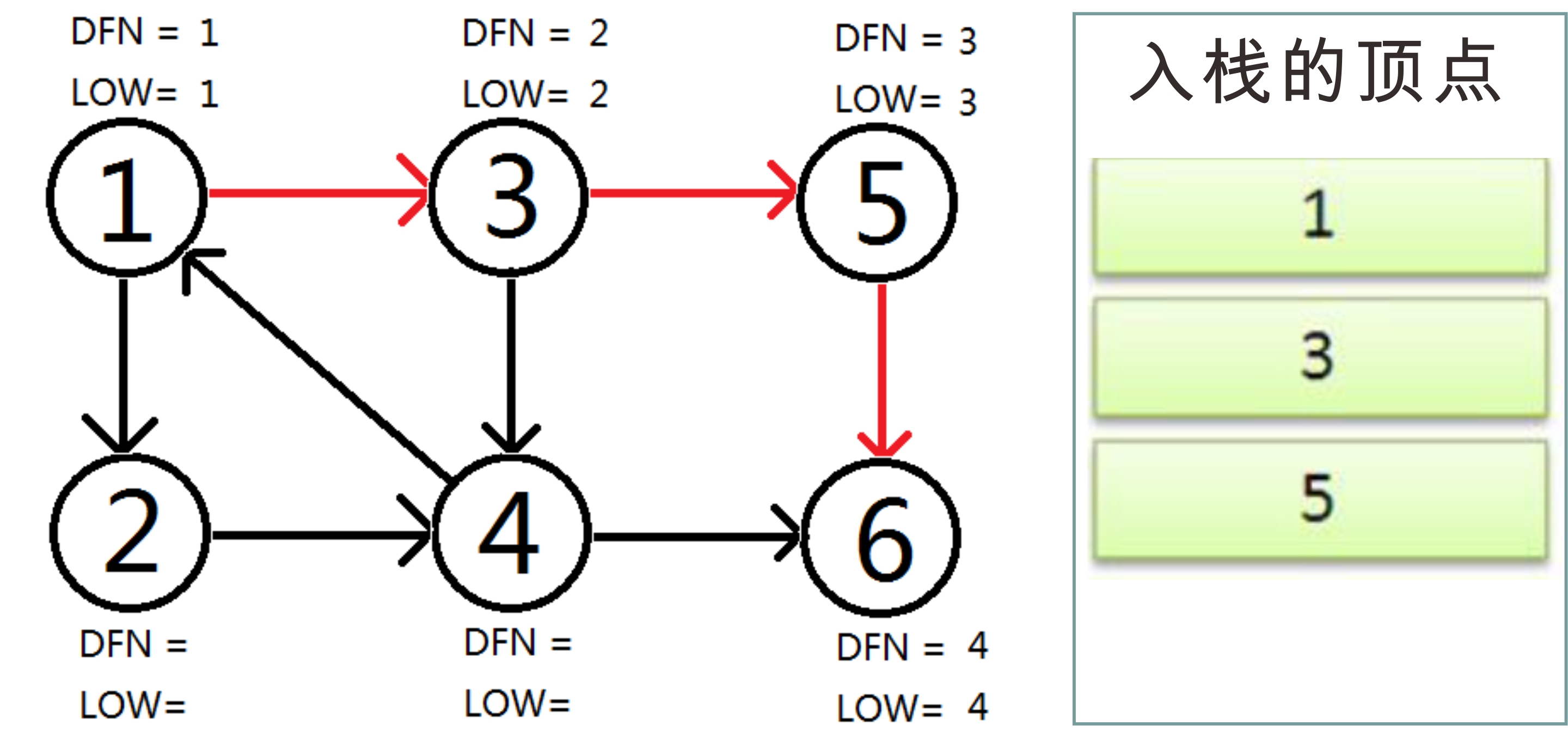
之后回溯到节点5，节点6被访问过了并出栈(pop)了，所以它也没有能访问的边了，

那么 DFN［5］＝＝LOW［5］，{5} 也是一个强连通分量，弹出5

目前栈的节点有： 1  3

 

返回节点3，继续搜索到节点4，节点4是新节点，设DFN[4]=LOW[4]=5并把4加入堆栈。

DFN［4］＝LOW［4］＝ ＋＋index －－－－－5

入栈 1  3   4  见下图：

 

 

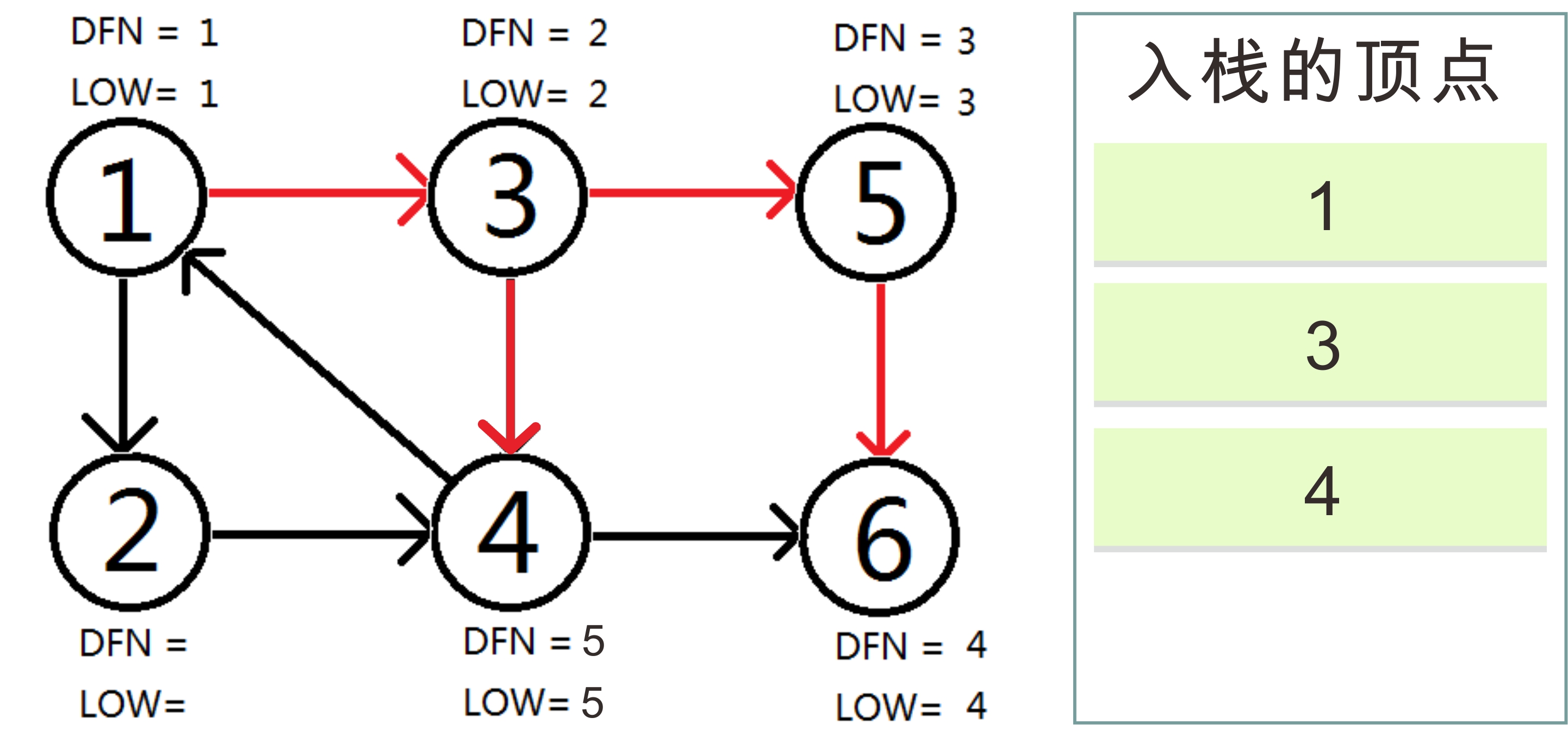
继续节点4往下找，找到了节点1 。

因为1号节点还在栈中，那么就代表着栈中的现有的所有元素构成了一个强连通图

（仔细想想、、兜了一圈又回到起点1）

 

回溯到节点4，更新 LOW[4]的值： LOW[4]= min(LOW[4], DFN[1])   值更新为1

再接着访问4的下一个节点6，节点6 被访问过并POP了，就不用管它了。

再回溯到节点3，更新 LOW[3]的值： LOW[3]= min(LOW[3], LOW[4])   值更新为1

3号节点也没有能访问的下一个节点了。图如下： 

 

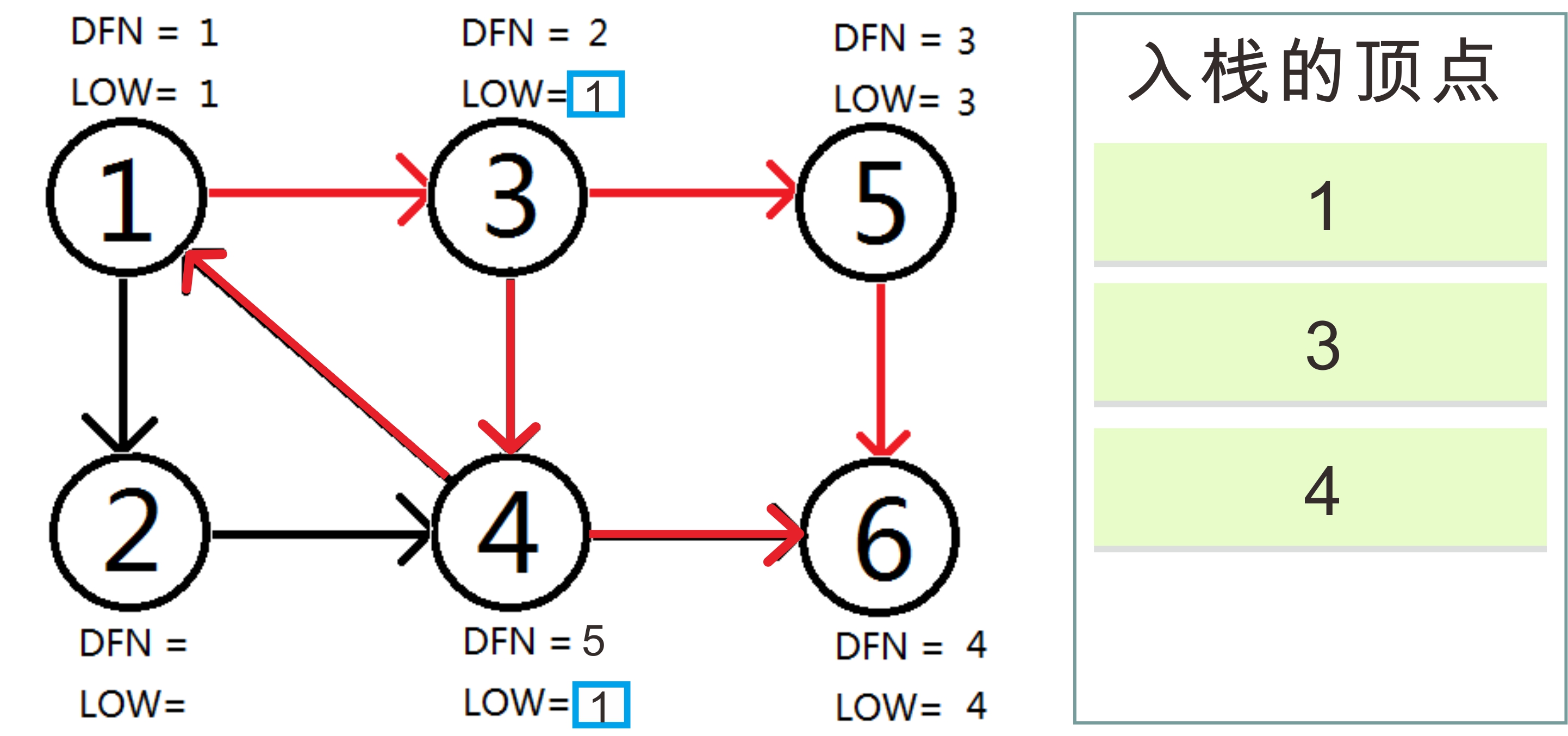
再回溯到节点1，更新 LOW[1]的值： LOW[1]= min(LOW[1], LOW[3])   值还是为1

节点1还有边没有走过。发现节点2，访问节点2，节点2是新节点，放入栈中

DFN［2］＝LOW［2］＝＋＋index －－－－6

入栈 1  3  4  2 

由节点2，走到4，发现4被访问过了，4还在栈里，

回溯到节点2 更新LOW[2] = min(LOW[2], DFN[4])     LOW［2］＝5

节点2也没有可访问的下一个节点了。

再回溯到节点1 更新LOW[1] = min(LOW[1], LOW[2])     LOW［1］＝1

这时我们发现LOW[1]==DFN[1]   说明以1为 根节点 的强连通分量已经找完了。

将栈中1，3，4，2全部节点都出栈。{1，3，4，2} 是强连通分量。图如下

            

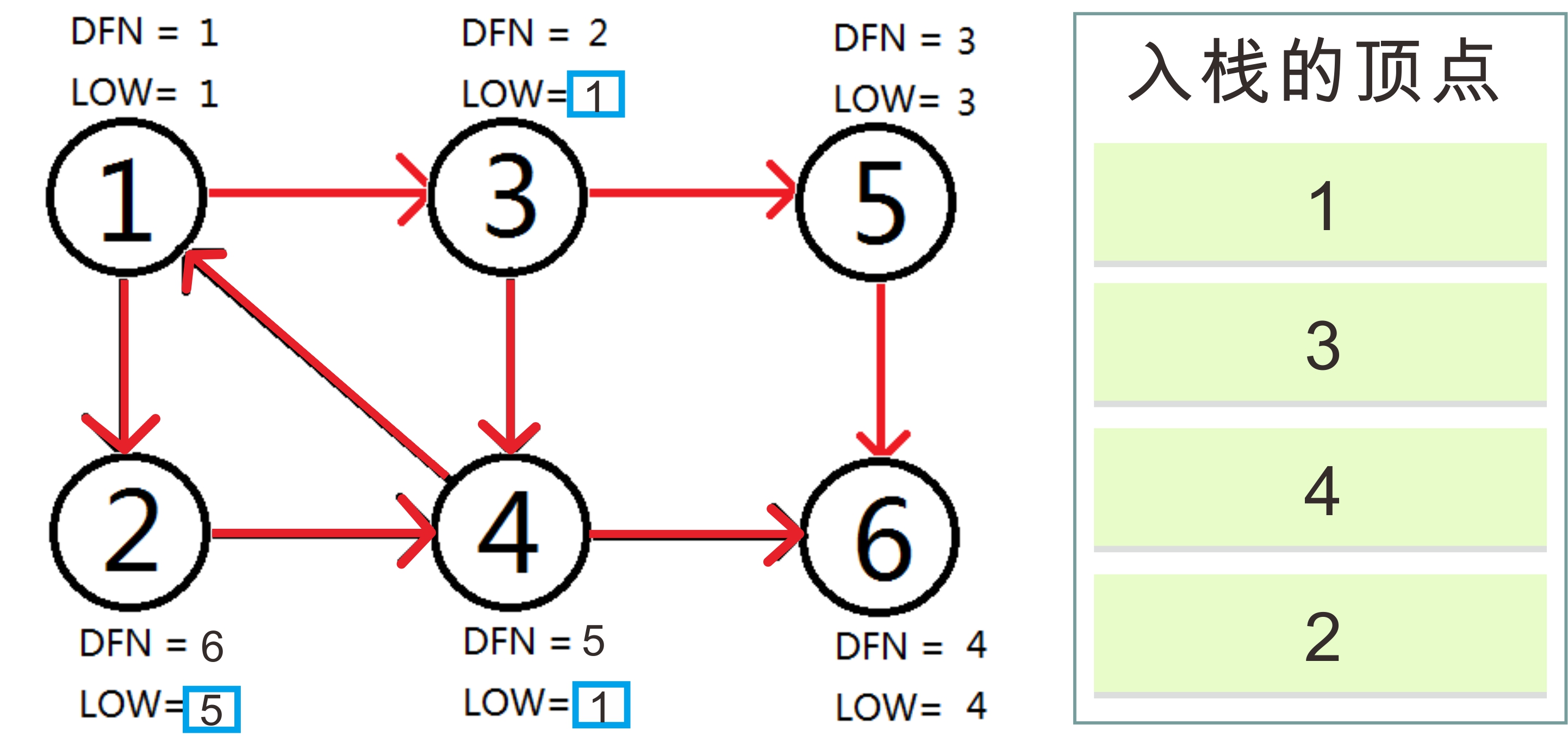
至此，算法结束。经过该算法，求出了图中全部的三个强连通分量{1,3,4,2},  {5},  {6}。

可以发现，运行Tarjan算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为O(N+M)。

实战：（后面有Tarjan算法的伪代码及模板，可以参考）

P1726 上白泽慧音   https://www.luogu.org/problemnew/show/1726

P2661 信息传递     https://www.luogu.org/problemnew/show/2661

P3379 LCA  Tarjan算法  https://www.luogu.org/problemnew/show/3379

P1262 间谍网络 （提示：可用Tanjan缩点） https://www.luogu.org/problemnew/show/1262

P3387 【模板】缩点   https://www.luogu.org/problemnew/show/3387 

以下4道题是北京大学的是英文题，如不明白意思可看下面的翻译：

题解 http://blog.csdn.net/u012469987/article/details/51292558#poj-1236-network-of-schools 

http://poj.org/problem?id=2186     http://poj.org/problem?id=1236

http://poj.org/problem?id=1904      http://poj.org/problem?id=1330 

 

 

接下来我们讨论一下Tarjan算法另外能够干一些什么：

既然我们知道，Tarjan算法相当于在一个有向图中找有向环，那么我们Tarjan算法最直接的能力就是缩点辣！缩点基于一种染色实现，我们在Dfs的过程中，尝试把属于同一个强连通分量的点都染成一个颜色，那么同一个颜色的点，就相当于一个点。

比如刚才的实例图中缩点之后就可以变成这样： 

 

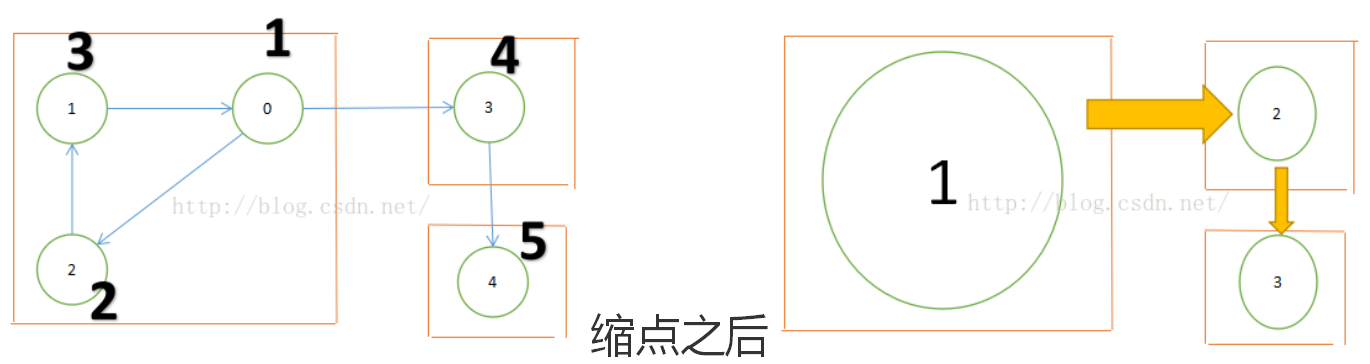
将一个有向带环图变成了一个有向无环图(DAG图)。很多算法要基于有向无环图才能进行的算法就需要使用Tarjan算法实现染色缩点，建一个DAG图然后再进行算法处理。在这种场合，Tarjan算法就有了很大的用武之地！

那么这个时候 ，我们再引入一个数组color【i】表示节点i的颜色，再引入一个数组stack【】实现一个栈，然后在Dfs过程中每一次遇到点都将点入栈，在每一次遇到关键点的时候将栈内元素弹出，一直弹到栈顶元素是关键点的时候为止，对这些弹出来的元素进行染色即可。

 

缩点代码实现： 

void Tarjan(int u)  //此代码仅供参考
{
    vis[u]=1;
    low[u]=dfn[u]=cnt++;
    stack[++tt]=u;
    for(int i=0;i<mp[u].size();i++)
    {
        int v=mp[u][i];
        if(vis[v]==0)Tarjan(v);
        if(vis[v]==1)low[u]=min(low[u],low[v]);
    }
    if(dfn[u]==low[u])
    {
        sig++;
        do
        {
            low[stack[tt]]=sig;
            color[stack[tt]]=sig;
            vis[stack[tt]]=-1;
        }
        while(stack[tt--]!=u);
    }
}

 

 

Tarjan算法伪代码参考：

//注意，v指的是u能达到的下一个节点
tarjan(u){
　　DFN[u]=Low[u]=++Index   // 为节点u设定次序编号和Low初值
　　Stack.push(u)           // 将节点u压入栈中
　　for each (u, v) in E     // 枚举每一条边
　　　　if (v is not visted) // 如果节点v未被访问过
　　　　　　　　tarjan(v) // 继续向下找
　　　　　　　　Low[u] = min(Low[u], Low[v])
　　　　else if (v in S) // 如果节点u还在栈内
　　　　　　　　Low[u] = min(Low[u], DFN[v])
　　if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根
　　repeat v = S.pop  // 将v退栈，为该强连通分量中一个顶点
　　print  v
　　until (u== v)
}

 

 

Tanjan算法模板：

void Tarjan ( int x )
 {
  dfn[ x ] = ++dfs_num ;
  low[ x ] = dfs_num ;
  vis [ x ] = true ; //是否在栈中
  stack [ ++top ] = x ;
  for ( int i=head[ x ] ; i!=0 ; i=e[i].next )
      {
          int temp = e[ i ].to ;
          if ( !dfn[ temp ] )
           {
             Tarjan ( temp ) ;
              low[ x ] = gmin ( low[ x ] , low[ temp ] ) ;
           }
            else if ( vis[ temp ])low[ x ] = gmin ( low[ x ] , dfn[ temp ] ) ;
      }
      if ( dfn[ x ]==low[ x ] )            //构成强连通分量
      {
            vis[ x ] = false ;
             color[ x ] = ++col_num ;    //染色
             while ( stack[ top ] != x )  //清空
             {
              color [stack[ top ]] = col_num ;
             vis [ stack[ top-- ] ] = false ;
             }
                 top -- ;
       }
}

 

Tanjan算法另一个模板：

#define M 5010       //题目中可能的最大点数
int STACK[M],top=0;  //Tarjan算法中的栈
bool InStack[M]; //检查是否在栈中
int DFN[M];    //深度优先搜索访问次序
 
int Low[M];  //能追溯到的最早的次序
int ComponentNumber=0;  //有向图强连通分量个数
int Index=0;  //索引号
vector<int> Edge[M];  //邻接表表示
vector<int> Component[M];  //获得强连通分量结果
int InComponent[M];  //记录每个点在第几号强连通分量里
int ComponentDegree[M]; //记录每个强连通分量的度
 
void Tarjan(int i)
{
    int j;
    DFN[i]=Low[i]=Index++;
    InStack[i]=true;STACK[++top]=i;
    for (int e=0;e<Edge[i].size();e++)
    {
        j=Edge[i][e];
        if (DFN[j]==-1)
        {
            Tarjan(j);
            Low[i]=min(Low[i],Low[j]);
        }
        else
            if (InStack[j]) Low[i]=min(Low[i],DFN[j]);
    }
    if (DFN[i]==Low[i])
    {
        ComponentNumber++;
        do{
            j=STACK[top--];
            InStack[j]=false;
            Component[ComponentNumber].
            push_back(j);
            InComponent[j]=ComponentNumber;
        }
        while (j!=i);
    }
}

 

Tarjan算法裸代码：

输入：

一个图有向图。

输出：

它每个强连通分量。

这个图就是刚才讲的那个图。一模一样。

input:

6 8

1 3

1 2

2 4

3 4

3 5

4 6

4 1

5 6

output:

6

5

3 4 2 1 

#include<cstdio>
 #include<algorithm>
 #include<string.h>
 using namespace std;
 struct node
{
     int v,next;
 }edge[1001];
 int DFN[1001],LOW[1001];
 int stack[1001],heads[1001],visit[1001],cnt,tot,index;
void add(int x,int y)
{
     edge[++cnt].next=heads[x];
     edge[cnt].v = y;
     heads[x]=cnt;
    return ;
 }
 void tarjan(int x)  //代表第几个点在处理。递归的是点。
 {
     DFN[x]=LOW[x]=++tot; //新进点的初始化。
     stack[++index]=x; //进栈
     visit[x]=1;  //表示在栈里
    for(int i=heads[x];i!=-1;i=edge[i].next)
     {
         if(!DFN[edge[i].v]) //如果没访问过
{   
            tarjan(edge[i].v);  //往下进行延伸，开始递归
             LOW[x]=min(LOW[x],LOW[edge[i].v]);//递归出来，比较谁是谁的儿子／父亲，就是树的对应关系，涉及到强连通分量子树最小根的事情。
           }
        else if(visit[edge[i].v ])//如果访问过，并且还在栈里
{  
             LOW[x]=min(LOW[x],DFN[edge[i].v]);//比较谁是谁的儿子／父亲。就是链接对应关系
          }
     }
     if(LOW[x]==DFN[x]) //发现是整个强连通分量子树里的最小根。
    {
         do{
            printf("%d ",stack[index]);
             visit[stack[index]]=0;
             index--;
         }while(x!=stack[index+1]);//出栈，并且输出。
         printf("\n");
     }
     return ;
 }
 int main()
 {
     memset(heads,-1,sizeof(heads));
     int n,m;
     scanf("%d%d",&n,&m);
    int x,y;
     for(int i=1;i<=m;i++)
     {
         scanf("%d%d",&x,&y);
        add(x,y);
     }
    for(int i=1;i<=n;i++)
         if(!DFN[i])  tarjan(i);//当这个点没有访问过，就从此点开始。防止图没走完
    return 0;
 }