结对编程项目总结(core2组)
结对编程项目总结(core2组)
作业---四则运算(Core 第二组)
----by 吴雪晴 PB16061514
齐天杨 PB16060706
一、项目简介
项目的任务为制作一个给(貌似是?)小学生用的四则运算出题软件,我们的组别为Core组,也就是负责随机生成四则运算表达式,
并将其封装成dll模块,供UI组使用
二、GITHUB地址
https://github.com/shirley-wu/hw2-Core 代码
https://github.com/shirley-wu/hw2-CoreDll Dll
三、功能介绍
1.
2. 将四则运算的计算功能包装在一个模块中( DLL)
3. 将Core模块通过一定的API 接口( Application Programming Interface ) 来和其他组的模块( UI )交流
四、代码主要架构
初始设计:
一开始,我们错误地理解了题意,认为要实现两个独立的功能:对用户提供的表达式进行求值,和按照设置随机生成表达式。
对于表达式求值模块,我们打算用最传统的方法,用运算符栈和运算数栈两个栈进行计算。不过非常遗憾后来才意识到这个模
块不用实现,因而花费了很多无用功。
对于生成表达式模块,考虑到题目要求较高的灵活性,我们打算使用二叉树表示算式,通过递归实现算式的生成、求值及翻
译成字符串。在这个部分,我们最初打算划分成许多个模块。从上而下,首先是Generator模块,实现与用户的交互、二叉树
的生成;然后是Setting类,考虑到各种设置信息很多,用一个类负责保存各种设置信息和解析xml;其次是Node,即二叉树结
点;然后是Num类,用来将三种类型,即整数、小数、分数,封装在一个对象里,从而上层可以直接调用;最后实现分数类Frac
tion,封装了各种运算。
我们的代码可以主要的分为如下几个模块:
1、生成:
Generate模块:调用Node与Setting,按照不同的设置生成表达式。
有两种生成方式:
1. generate_tree,递归随机生成操作符、操作数,从而递归生成二叉树。
2. generate_int_node(int val),通过给定的值配凑生成一个表达式,但只能生成整数表达式。
这个模块提供了std::string接口、char数组接口与文件接口,具体见api。
Node * generate_tree(int limit, bool num_en) {
Node * p;
NODETYPE type;
if (limit == 1) {
if (num_en == false) throw("wtf");
else type = NUM;
}
else if (num_en == false) type = OPR;
else type = NODETYPE(rand() % TYPENUM);
if (type == NUM) {
p = Node::randNum();
}
else {
int v = rand() % OPRNUM;
OPRTYPE opr = randomopr();
p = new Node(opr);
int limit1, limit2;
if (limit == 2) limit1 = limit2 = 1;
else {
limit1 = (rand() % (limit - 2)) + 1;
limit2 = limit - limit1;
}
if (setting.type == INT && opr == DIV) {
int denom = rand() % (setting.num_max - 1) + 1;
int numer = (rand() % (setting.num_max / denom)) * denom;
p->set_lchild(create_int_node(numer, limit1));
p->set_rchild(create_int_node(denom, limit2));
p->calc_val();
}
else {
if (opr == POW) {
int v = rand() % 5;
p->set_lchild(generate_tree(limit1));
p->set_rchild(create_int_node(v, limit2));
while (true) {
try {
p->calc_val();
}
catch (Overflow& e) {
v--;
p->set_rchild(create_int_node(v, limit2));
continue;
}
catch (...) {
throw;
}
break;
}
}
else {
p->set_lchild(generate_tree(limit1));
p->set_rchild(generate_tree(limit2));
while (true) {
try {
p->calc_val();
}
catch (Overflow& e) {
p->set_lchild(generate_tree(limit1));
p->set_rchild(generate_tree(limit2));
continue;
}
catch (Zeroerror& e) {
p->set_lchild(generate_tree(limit1));
p->set_rchild(generate_tree(limit2));
continue;
}
catch (Negerror& e) {
p->exchange_lr();
continue;
}
catch (Exaerror& e) {
p->set_lchild(generate_tree(limit1));
p->set_rchild(generate_tree(limit2));
continue;
}
catch (...) {
throw;
}
break;
}
}
}
}
return p;
}
以及节点的构造:
Node模块:二叉树结点类。有操作符结点与操作数结点两种,操作数结点又分整数、小数、分数三种。有递归计算、递归解析
为表达式和判断两个表达式是否等效功能。
对于判断表达式是否等效,思路如下:首先判断根节点是否相等,然后如果两子树非空,递归分别判断两子树是否相等。假如
两子树不等,但根节点为+或*,则交换两子树,分别递归判断是否相等(即,加法与乘法可交换)。
Node * create_int_node(int a, int limit) {
if (a < 0) throw(Negerror());
Node *p = NULL;
NODETYPE type;
OPRTYPE tool;
if (limit == 1 || (setting.opr[(int)SUB] == false && setting.opr[(int)ADD] == false)) {
type = NUM;
}
else if (a == 0) {
if (setting.opr[(int)SUB] == false) type = NUM;
else {
type = NODETYPE(rand() % TYPENUM);
if (type == OPR) tool = SUB;
}
}
else {
type = NODETYPE(rand() % TYPENUM);
if (type == OPR) {
if (setting.opr[(int)SUB] == false) tool = ADD;
else if (setting.opr[(int)ADD] == false) tool = SUB;
else tool = (rand() % 2) == 0 ? ADD : SUB;
}
}
if (type == NUM) {
p = new Node(a);
}
else {
int limit1, limit2;
if (limit == 2) limit1 = limit2 = 1;
else {
limit1 = (rand() % (limit - 2)) + 1;
limit2 = limit - limit1;
}
int lchnum, rchnum;
if (tool == ADD) {
lchnum = rand() % a;
rchnum = a - lchnum;
p = new Node(ADD);
p->set_lchild(create_int_node(lchnum, limit1));
p->set_rchild(create_int_node(rchnum, limit2));
p->calc_val();
}
else {
rchnum = rand() % (setting.num_max - a);
lchnum = a + rchnum;
p = new Node(SUB);
p->set_lchild(create_int_node(lchnum, limit1));
p->set_rchild(create_int_node(rchnum, limit2));
p->calc_val();
}
}
return p;
}
2、对操作数的计算(包括整数,小数,分数3种类型)
其中,Fraction模块:和最初设想一样,封装分数的运算与显示功能
friend void add(const Fraction& f1, const Fraction& f2, Fraction& f);
friend void sub(const Fraction& f1, const Fraction& f2, Fraction& f);
friend void mul(const Fraction& f1, const Fraction& f2, Fraction& f);
friend void div(const Fraction& f1, const Fraction& f2, Fraction& f);
friend void pow(const Fraction& f1, int p, Fraction& f);
bool operator==(const Fraction& f) const;
friend std::ostream& operator<<(std::ostream& os, const Fraction& f);
int to_str(char * s, int start, int end) const;
3、对参数的设置
Setting模块:保存各个变量值,通过几个函数进行设置,有输入检查,如果输入不合法就丢弃输入、采用默认值。本来我们打算用xml或json,但后来发现参数不多,而且ui组大多数没有使用xml / json,因此我们也没有提供相应接口。
typedef struct Setting {
int num_max = 1000;
// maximum of num
int num_limit = 20;
// limit of nums
int exp_num = 5;
// number of expressions
NumType type = DOUBLE;
// type of number
int precision = 2;
// precision of double
int pow_max = 5;
// max power exp
bool opr[OPRNUM] = { true, true, true, true, false };
// available opr
int opr_num = 4;
// number of available opr
bool power_signal = true;
// way to show power: true -> '^', false -> '**'
} Setting;
4、DLL文件的对接
CORE_DLL_API void set(int num_max, int num_limit, int exp_num, int type = 0, int precision = 2); CORE_DLL_API void set_precision(int precision); CORE_DLL_API void set_opr(bool add, bool sub, bool mul, bool div, bool pow); CORE_DLL_API void set_power_signal(bool s); CORE_DLL_API void generate(); CORE_DLL_API void clear(); CORE_DLL_API bool get_exp(int i, std::string& s, std::string& result); CORE_DLL_API bool get_expression(int i, char *s, int size); CORE_DLL_API bool get_answer(int i, char *s, int size); CORE_DLL_API bool exp_to_file(const char* dir); CORE_DLL_API bool ans_to_file(const char* dir);
五、样例输出(包括文件输出):
1、小数
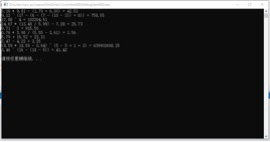

2、整数
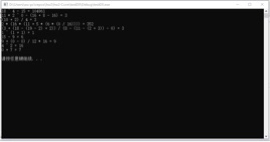

3、分数
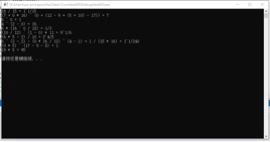

六、过程中产生的问题
我们遇到的第一个问题在于整体结构太过于繁琐,Generator, Setting, Node, Num, Fraction,五个模块、四层封装,太过于复杂;
况且Num这一层次只是判断一下操作数类型,似乎比较鸡肋。经过讨论之后,我们去掉了Num这一层次,直接在Node中保存操作数信息。
我们遇到的第二个问题在于,突然从助教那里得知整数除法应该整除。我们原本考虑丢弃不能整除的式子重新生成,后来发现这样速度太慢。
最后,我们决定放弃绝对的随机性,而选择配凑。我们考虑了好几种配凑方式,最后决定对于整数的除法,通过给定一个整数值、配凑
生成表达式的方式,生成被除数与除数的算式。
事实上,我们也考虑过整体更改为配凑方式,但配凑方式逻辑较复杂,而且难以处理乘方,所以我们只打算对整数除法进行配凑。
不过到了后来,我们惊喜地发现乘方的幂次也可以配凑。
我们遇到的第三个问题在于对于dll的使用非常不熟悉。我们为此研究了很久,才终于攻克这一关。
首先,我们对于dll的概念非常不了解,为了了解这些基础概念就花了很久。
然后,非常尴尬地,我们原本打算导出Generator类,但是用dll导出类非常复杂。有两种可选的方案,一是将Generator及其属性的类全
部导出,这样一来会暴露自己的内部实现,违反了封装原理;另外一个是导出抽象类,但是这个概念我们两人都不太熟悉,而且这样会增加一
层调用,加大代码复杂度。
在我们和ui进行了进一步沟通之后,我们了解到ui其实只需要函数;再加上我们编码中也出现了不知道如何让Setting对象成为全局对象这一问题,
我们决定直接使用全局变量与c函数接口。
最后,我们生成dll后不知如何运行。查找了很多资料之后,我们才学会通过另一个项目,即testDll项目,调用自己生成的dll。
七、本次结对编程的心得
1、两个人一起工作能增加每个人的工作积极性。因为在面对问题的时候,你并不是一个人,总会有人一起分担,共同尝试新的策略,因此,
在爆肝代码的路上你并不孤独。 (只要2个人有一个会的)
2、两个人一起工作需要互相配合,如果其中有人想去偷懒去干别的,那么就会拖延工作进度,这样谁的面子上也说不过去。
3、在编程中,两个人之间毫无保留的相互讨论,可以更快更有效地解决问题,互相请教对方,可以得到能力上的互补,而且可以从对方那里得到很
多启发,学习到平常自学时学习不到的东西,开拓了自己的视野,提升了自己的素质。
4、小组两人在写代码时可以互相监督工作,这样就可以增强代码的质量,并有效的减少 BUG,有时候一个人写代码往往一个极小极弱智的错误
都会让你卡上一天,然而只要自己的队友看一眼,说一句话,这个小问题可能就解决了。
5、通过本次结对编程,使我们对编程的思想理解的更为深厚,让我们更好的理解了合作互助的关系,在以后的编程道路中可以更好的为对方考虑,
两个人可以取长补短,个用所长。
6、本次结对编程的过程中我们曾经很多次遇到了困难。包括题目理解错误,BUG无法改正等等等等,但是我们不为艰难,一部一部把问题细化,
逐个击破了存在的问题,虽然我们也曾感到无助,虽然我们也曾爆肝代码,在如此繁忙的一周里如期完成了既定的任务。可以说结对编程使我们
的意志力和内心的坚定得到了锻炼。
7、由于本次任务不光是要写完代码,完成所有的基本功能,更是要与下端的UI组进行对接,在对接的过程中由于大家的代码风格各异,所使用的
格式也全然不同,这给我们的对接造成了很大的不便。但是我们本着对自己也是对别人的代码的认真负责的态度,认真听取UI组成员的反馈意见
并及时修改我们的代码,增强我们代码的鲁棒性,最终达到脍炙人口的效果。在这个过程中,我们对事物的责任心得到了充分的历练,对以后接待
客户也有了一定的了解与认识。
八、对这门课的感想
1、感觉这门课对编程和自学的能力要求较高,比较适合编程基础比较弱的同学借此强化一下编程的能力(比如我)。另外,特别值得称赞的一点是这
门课的任务布置模式,同真正的工作岗位上的任务模式比较相近,有助于以后在工作岗位上的驾轻就熟。这是在科大这种可能对外接触机会比较少的
地方来说是一个非常宝贵的经历。
2、这门课程是我见过授课形式比较新颖的课堂之一,老师通过读书笔记的形式强迫你去看一些平时自己没时间关注的或是自己偷懒不想去看的书籍,
以前我会觉得这是在浪费时间,但现在仔细读过这些书籍之后会发现这些书籍带给我的不仅仅是一些关于管理软件工程这一方面的知识,更多的是
对你人生路的一种指引,对你心灵的一种启迪。在读书的时候经常可以联系到自己的实际生活,给自己以警醒给自己以鞭策的动力。这也是其他课
程所学习不到的东西。
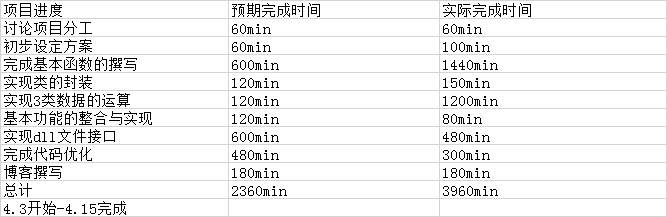
PSP表格
项目分工:
基本函数:calc(qi)\generate(wu)
类的封装(wu)
实现3类数据运算(wu)
基本功能的整合与实现(wu+qi)
实现DLL(wu)
代码优化(qi+wu)
博客撰写(qi)
|
||
|
|
||




