“学习流形”的初认识
本文主要围绕学习流形这个概念来讲,而不是流形学习。流形学习仅仅是利用流形局部性质(邻域)来学习流形的一个领域,而学习流形则是更加宽泛的一种思想理念。下面首先简单介绍一下我对流形这一概念的认识,然后讲一下机器学习中学习流形的动机,最后结合不同方法来讲如何学习流形。
一、什么是流形
我接触流形这一概念已经半年多了,从最开始的仰望到慢慢攀爬,现在已经逐渐麻木了。要全面地去弄清楚流形是个什么东西是极其困难的,因为它是数学几何里的抽象概念,特别是在维度特别高的情况下,要想象出它的样子根本不可能,而且它还有很多的复杂性质。但是,如果它仅用来机器学习的话,我们只要知道它的简单定义和一些基础性质就行了。
1、简单定义
首先,我们要知道流形是一个空间,而不是一个类似于正方体这样的简单几何物体。这一点很重要,我们可以拿欧式空间去和流形对比,两者都是空间,但前者是直线、平面等概念的推广,而后者是欧式空间中曲线、曲面等概念的推广。那么两者有什么关系呢?因为直线、平面等概念可以看成对应维度的曲线、曲面等的特例,所以欧式空间相应地可以看成流形的一个特例,叫线性流形。
一般大家研究流形是为了解决非线性问题,所说的流形也都默认是非线性流形。但本文为了从学习流形这个大的理念来讨论,所以下面将流形细分为线性流形(欧式空间)和非线性流形。
再说一说非线性流形,我们可以粗暴地去理解,将非线性流形看成欧式空间被扭曲的结果,而用来描述欧式空间的直角坐标系中的轴也相应地被掰弯了。举一个二维的例子,展平的一块抹布,可以看成二维欧式空间,当抹布被扭一扭后,它就变成了一个非线性流形。
2、局部性质
流形的局部是具有欧式空间性质的。就像曲线无限放大后,局部是直线一样,流形无限小的局部也可以看成欧式空间,因此流形局部具有欧式空间性质。地球表面就是一个稍微复杂的例子,从远处看,地球表面近似一个球面,但从地球上的我们来看,地球表面是一个平面。从这个性质出发,一般的流形可以通过把许多平直的片折弯并粘连而成,而这些片则被称为坐标卡(坐标图)。


3、测地线距离
测地线距离是用来度量流形中的距离的。当所在的空间是欧式空间(线性流形)时,测地线距离也就是我们常用的欧式距离;但当空间是非线性流形时,测地线距离不再是欧式距离。还是地球表面的那个例子,假如限定在表面(一个非线性流形)去衡量南北极的距离,我们是不可能直接拉一根直线穿过地心去测量的,只能贴着表面去找最短距离,找出来的这个距离就叫测地线距离。
简单来说,欧式距离不能满足非线性流形的约束,所以有了测地线距离。就像地球表面上南北极的欧式距离不满足球面约束,越出了球面这个空间。
4、切平面
流形的一个重要特征是流形可看作切平面的集合。d 维流形上的一点 x 的切平面由能张成流形上允许变动的局部方向的 d 维基向量给出,而这些局部方向决定了我们能如何微小地变动点 x 而保持于流形上。这里提到的切平面其实是我们用自编码器学习非线性流形所依赖的一个很重要的性质。
5、固有维数、嵌入维数、流形维数
- 固有维数:数据的固有性质,也是参数空间(能完整包含数据的维数最少的欧式空间)的维数。
- 嵌入维数:数据集能够完全嵌入且不损失信息的欧式空间的维数。(嵌入指一个数据结构经映射包含到另一个结构中)
- 流形维数:流形本身的维数,其大小等于自由度(用来完整描述数据所需的最少特征或变量)的个数。
关于这三者的关系,我们需要明确一下:嵌入维数 \( \geq \) 固有维数 \( \geq \) 流形维数。
具体解释一下,嵌入维数是取决于数据的嵌入空间的,而固有维数则是嵌入空间维数最小的时候的维数,也就是说固有维数是嵌入维数的下界。而对于流形维数,大部分人都认为固有维数等于流形维数,这其实是不严谨的。因为当流形具有环状结构时,流形维数是要小于固有维数的。还是举地球表面的例子,表面作为一个二维流形,其流形维数是 2 ,但是其固有维数却是 3 ,我们可以想象具有环状结构的地球表面是不能在不损失结构的情况下嵌入到二维欧式空间的。当然流形不具有环状结构时,本征维数还是等于流形维数的,总结来说,固有维数是流形维数的上界。
二、为什么要学习流形
这个问题其实摘要里已经简单说明了,因为流形分布定律,即高维数据往往位于一个低维流形上或附近,所以流形是数据最本质的空间信息。而我们机器学习目的就是为了从经验中去学习进而提高在任务上的性能,经验的形式往往又是以数据形式存在的,所以我们只要提取出数据的本质信息,就能更高效地去学习。
在当今数据爆炸的时代,维度灾难时常出现。以往在低维度适用的算法都效果很差或者计算代价过高。如果我们能学习到数据位于的那个低维流形,那么我们就可以在这个流形或其嵌入的参数空间里去运用原先的低维学习算法了。当下比较火的深度学习在高维数据中的表现优异,其很大程度上都是可以用流形来解释的。大家有兴趣的可以去看一下深度学习的几何观点。
总的来说,我们去学习流形可以减少计算机的内存负担和计算复杂度,并且可以使学习效果提升,特别是图像识别,手写体识别等。
三、怎么样学习流形
学习流形的算法一般有两种学习方式:
- 直接学习训练样本在流形上的嵌入,也就是计算出训练样本在参数空间的坐标表示。流形学习这个邻域就是基于这种学习的。
- 学习高维空间到参数空间的映射,典型代表是自编码器。
1、流形学习
流形学习作为机器学习的一个子领域,就是利用流形的局部性质来进行学习的,很明显的特征是流形学习算法都用到了最近邻图的概念。作为了一个比较年轻的邻域,流形学习也曾引起轰动,但是由于在实际非实验数据上的运用存在问题,以及深度学习的崛起,这个领域逐渐被冷淡。
流形学习算法主要分两类,一类是改造原来适用于欧式空间的算法,最典型的就是 Isomap 算法--先估计测地线距离来代替欧式距离,再应用 MDS 算法,可以看成对 MDS 的改进。第二类就是利用流形性质重新设计算法,代表的算法就是 LLE --针对保持邻域结构不变来构建目标函数。
这里我简单说一下流形学习这个领域学习的思想:
- 先用k近邻法构建*最近邻图**;
- 再提取流形的特征(测地线距离、领域结构等);
- 最后在保持这些性质的基础上去将数据映射到参数空间。
换个角度来说,可以简单理解成:首先学习数据所在的低维流形,然后将这个流形映射到参数空间。
介绍流形学习的博客有很多,我这里就不再多赘述了。有兴趣的可以去看看下面两个博客:
2、其他方法
学习线性流形
前面提到的流形学习虽然也能学习线性流形,但是其效果却没有线性方法好,计算复杂度也偏高。其实要学习线性流形,也就是学习欧式空间,最简单的线性因子模型就可以了。
线性因子模型是最简单的生成模型,一般用来描述数据的生成过程:
其中 x 是观察数据,W 是权重矩阵,b 是偏移量,noise 是对角化的且服从正态分布的噪声。可以从语言上来解释这个公式:我们观察到的数据向量 x 是通过独立的潜在因子 h 的线性组合再加上一定噪声获得的。
就拿线性因子模型里最简单的PCA来说,简单介绍一下它如何学习线性流形。
下图中有一个半薄饼状的概率分布区域,它是概率PCA的模型描述的生成数据概率分布的上半部分(下半部分对称),整个薄饼可以看成潜在因子所在的欧式空间(超平面)线性变换后加上噪声的多维正态分布形成的。图中为了可视化,把潜在因子所在空间看成三维的超平面(一般超平面是四维及以上的,我这里这么说是为了统一好理解),噪声是三维多维正太分布。而穿过薄饼的平面则是高维空间的线性流形(超平面),图中是三维超平面。
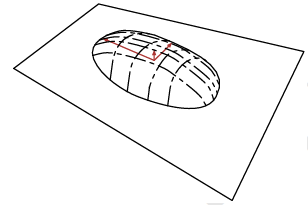
PCA是概率PCA生成模型中去除噪声的退化,其概率分布区域可以看成薄饼压扁,变成一个超平面。那么PCA则可以将薄饼压扁后通过训练数据来调整权重和偏移量参数,然后将模型描述的超平面与流形这个超平面贴合(其实叫对准更加恰当)。贴合后,我们就可以得到高维空间到参数空间的映射了。
学习非线性流形
自编码器可以依据两种动力去学习非线性流形:一种动力是对自身的重构误差要小,即解码器能恢复输入;第二种是通过约束(正则项)去学习对流形切平面上输入不敏感的函数。两种结合成一个目标函数,这样自编码器就可以学习非线性流形了。
能学习自编码器的有两种:
- 去噪自编码器:通过约束重构函数的梯度在数据点周围很小可以捕获流形的切平面结构。
- 收缩自编码器:与去噪自编码器目标相同,只不过手段是通过约束编码器学习到的函数在数据点周围梯度很小。
关于其他方法来学习流形这部分讲的比较简单抽象,其深入的理解将会在后续文章中涉及。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号