欧几里得及扩展欧几里得

欧几里得算法又称辗转相除法，主要用于求两数的最大公约数即gcd(a,b)。

欧几里得算法给出gcd（a，b）=gcd（b，a%b）（a>b)

下面我们给出证明:

首先我们设k为gcd(a,b)，则a=km，b=kn。

则a%b=a-c*b=km-c*kn=(m-cn)k

gcd(b,a%b)=gcd(kn,(m-cn)k)

由于k为a，b的最大公约数，所以n与m-cn互质，所以gcd(b,a%b)=gcd(a,b)=k。

程序实现：

int gcd(int a，int b)
{
    if (a < b) swap(a, b);
    return b==0?a:gcd(b, a % b);
}

//------------------------------------------------------------------这是分割线-------------------------------------------------------------------------------------------

 

扩展欧几里得算法

对于任意两个互质的a,b，总有gcd(a,b)=ax+by,扩展欧几里得算法可以用来求解x，y。

求法：

 

 

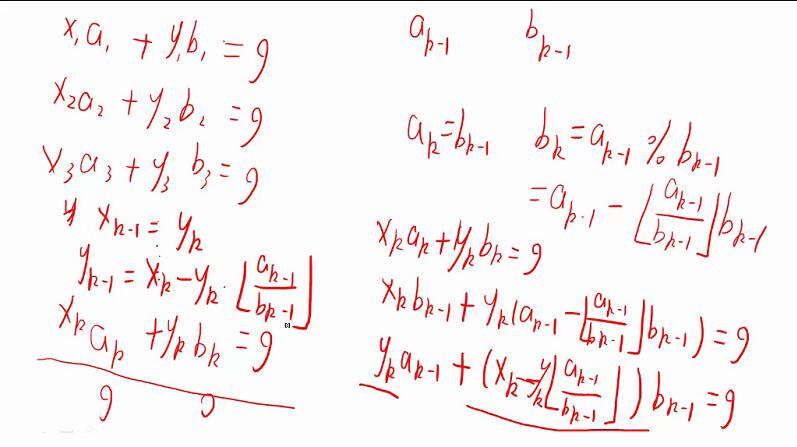
根据欧几里得算法可知gcd(a,b)=gcd(b,a%b)。

则bx‘+(a%b)y'=gcd(a,b)

将a%b=a-(a/b)*b带入得

ay'+b(x'-(a/b)*y')=gcd(a,b)

对于a，b而言，他们对应的x,y则分别为y',(x'-(a/b)*y')。

而当b=0时，a*1+b*0=gcd(a,b)。

下面是程序实现：

LL extgcd(LL a,LL b,LL& x,LL& y)
{
    if(b!=0)
    {
        LL d=extgcd(b,a%b,y,x);
        y-=(a/b)*x;
        return d;
    }
    else
    {
       x=1,y=0;
       return a;
    }
}