博客作业06--图
1.学习总结
1.1图的思维导图

1.2 图结构学习体会
- 深度遍历算法代码递归实现,广度遍历算法代码队列实现。
- Prim算法要弄清lowcost数组和ciosest数组的关系。
- Kruscal算法要弄清vest数组和E数组的关系。
- Dijkstra算法非常重要,dist,path,s三个数组之间的关系一定要弄懂。
- 拓扑排序算法中结构体中加入count元素,使得度的问题很容易解决了。
2.PTA实验作业
2.1 题目1:7-1 图着色问题
2.2 设计思路(伪代码或流程图)
用邻接矩阵创建图
输入颜色分配方案
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(存在边且颜色分配相同)
则分配失败
如果成功遍历
则颜色分配成功
2.3 代码截图
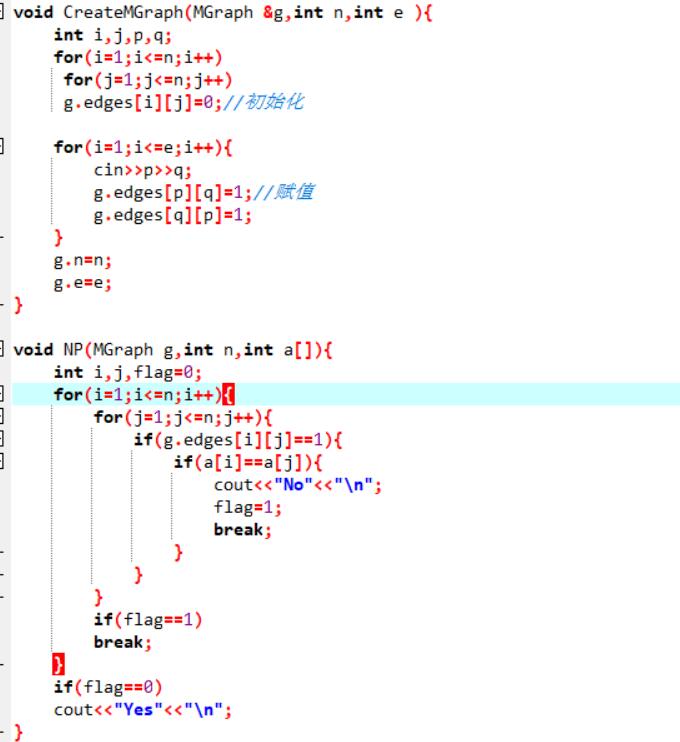

小于K种颜色的思路。
2.1 题目2: 排座位
2.2 设计思路(伪代码或流程图)
用邻接矩阵创建图
并增加一个矩阵,一个放朋友关系,一个放敌人关系
输入两位客人编号
if(朋友矩阵存在)
输出No problem
if(朋友矩阵和敌人矩阵都不存在)
输出OK
if(敌人矩阵存在)
判断是否存在相同朋友
if(存在)
输出OK but...
flag标志变1
循环结束flag为0
输出No way
2.3 代码截图
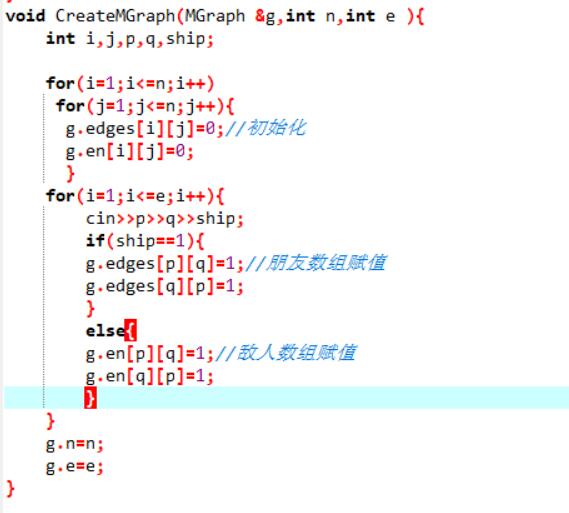

难点在于搞清两者关系后用代码来实现分类。
2.1 题目3:旅游规划
2.2 设计思路(伪代码或流程图)
在邻接矩阵结构体中新增一个money数组
创建图
利用Dijkstra算法
不同的是在加入dist和path数组的时候
如果若干条路径都是最短的
那么需要判断最便宜的一条路径
再加入dist和path数组
2.3 代码截图

本题是对于Dijkstra算法的拓展。
3.截图本周题目集的PTA最后排名
3.1 PTA排名(截图带自己名字的排名)

3.2 我的总分:219
4. 阅读代码
南将军统领着N个部队,这N个部队分别驻扎在N个不同的城市。
他在用这N个部队维护着M个城市的治安,这M个城市分别编号从1到M。
现在,小工军师告诉南将军,第K号城市发生了暴乱,南将军从各个部队都派遣了一个分队沿最近路去往暴乱城市平乱。
现在已知在任意两个城市之间的路行军所需的时间,你作为南将军麾下最厉害的程序员,请你编写一个程序来告诉南将军第一个分队到达叛乱城市所需的时间。
注意,两个城市之间可能不只一条路。
#include<stdio.h>
#include<string.h>
#define MAX 1000000
int city[101],map[1010][1010],d[1010],vis[1010],m;
void dijkstra(int start)
{
for(int i=1;i<=m;i++){
d[i]=map[start][i];
}
d[start]=0;
for(int i=1;i<=m;i++){
int min = MAX;
int x=0;
for(int j=1;j<=m;j++){
if(!vis[j]&&min>=d[j]){
min=d[j];
x=j;
}
}
vis[x]=1;
for(int j=1;j<=m;j++){
if(d[j]>min+map[x][j]){
d[j]=min+map[x][j];
}
}
}
}
int main()
{
int N,i,j;
scanf("%d",&N);
while(N--)
{
int n,p,q;
scanf("%d%d%d%d",&n,&m,&p,&q);
for(i=0;i<n;i++)
scanf("%d",&city[i]);
memset(map,MAX,sizeof(map));
memset(vis,0,sizeof(vis));
for(i=0;i<p;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
if(map[a][b]>c)
map[a][b]=map[b][a]=c;
}
int temp=MAX;
dijkstra(q);
for(i=0;i<n;i++)
if(temp>d[city[i]])
temp=d[city[i]];
printf("%d\n",temp);
}
return 0;
}





