因子分析如同主成分分析(PCA)一样也是一种降维的方法,其思想与PCA也是相似的。它们最直观的区别在于因子分析是要构造出新的因子构造因子模型,而并非仅仅将原始变量的线性组合表示新的综合变量(PCA的升级版)。
因子分析形式类似一个多元线性回归过程。首先要假象有一些公共因子和特殊因子,公共因子是不可观测的变量,而特殊因子是不能被公共因子包含的部分(随机部分),利用这些因子变量我们来线性表示原始变量,公共因子前的系数称为载荷因子。注意:因子分析与回归分析不同,因子分析中的因子是一个比较抽象的概念,而回归因子有非常明确的实际意义;另外,回归系数和载荷因子的形式和含义是截然不同的。
因子模型形式:
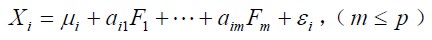
这里做如下几个假设:var(F)=1,公共因子和特殊因子不相关,各公共因子和特殊因子之间也不相关。
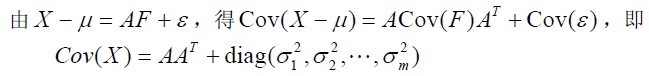
对变量X进行标准化变换,则Cov(X)等于X的相关系数矩阵R。于是:
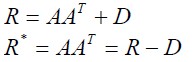
我们需要利用上式解出A。如果没有D,能不能解出A呢?此时只用将R进行对角化,就可以求了(这里体现了与PCA的联系之处)。现在由于D的存在,所以理论上我们只能对R*进行对角化才能求A,不幸的是R*是不知道的,很容易想到需要估计D。进一步思考,D只是个对角阵,所以其实上需要估计的就是R*上对角线上的值(其余值与R是一样的,也就是说样本方差部分被分解成两个部分了)。如果假设R*对角线为1,实际上就是没有D的情况,这就是主成分分析!当然,也可以利用其它方法来估计R*的对角线。这样就可以得到公共因子前的系数A(载荷因子)。
新的问题又出现了,这些公共因子是我们事先假设的,它们究竟在实际问题中代表什么含义?载荷矩阵不是唯一的,那么哪个载荷矩阵才是我们需要的?如何理解利用因子分析对个变量进行分类?这些下节将会详细叙述。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号