ISLR第10章 Unsupervised Learning
Unsupervised learning, a set of statistical tools intended for the setting in which we have only a set of features
X1,X2, . . . , Xp measured on n observations. We are not interested in prediction, because we do not have an
associated response variable Y .
下面主要讲了10.1主成分分析和10.2聚类分析。
10.1 Principal Components Analysis(主成分分析PCA)
PCA is an unsupervised approach, since it involves only a set of features X1,X2, . . . , Xp, and no associated response Y .
Apart from producing derived variables for use in supervised learning problems, PCA also serves as a tool for data visualization
(visualization of the observations or visualization of the variables).
10.1.1 What Are Principal Components?
The idea is that each of the n observations lives in p-dimensional space, but not all of these dimensions are equally interesting.
PCA seeks a small number of dimensions that are as interesting as possible, where the concept of interesting is measured by
the amount that the observations vary along each dimension. Each of the dimensions found by PCA is a linear combination
of the p features.

The second principal component scores z12, z22, . . . , zn2 take the form
![]()
biplot(双标图):
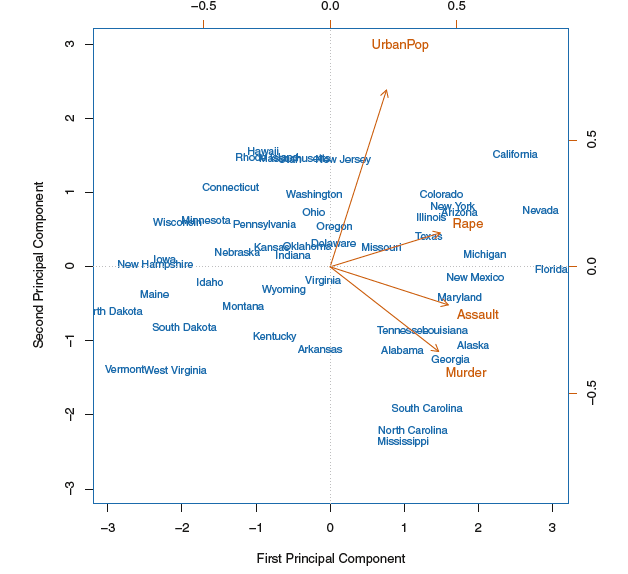

主成分荷载向量定义为变量空间上数据变异程度最大的方向,而将主成分得分定义为在这些方向上的投影。
主成分的另一种解释:主成分提供了一个与观测最为接近的低维线性空间。

变量的标准化:在进行PCA之前,变量应该标准化使均值为零,标准差为1。
主成分的唯一性:在不考虑符号变化的情况下,每个主成分载荷向量都是唯一的。
方差的解释比例(PVE):

In total, there are min(n − 1, p) principal components, and their PVEs sum to one.
Deciding How Many Principal Components to Use:
方法:scree plot(碎石图)

10.2聚类分析
数据聚类则是将本没有类别参考的数据进行分析并划分为不同的组,即从这些数据导出类标号。
分为K均值聚类和系统聚类法
10.2.1 K均值聚类
K均值聚类是一种把数据集分成K个不重复类的简单快捷的方法。在进行K均值聚类时,必须首先确定K的值。

The idea behind K-means clustering is that a good clustering is one for which the within-cluster variation is as small as possible.
The within-cluster variation for cluster Ck is a measure W(Ck) of the amount by which the observations within a cluster differ
from each other. Hence we want to solve the problem:
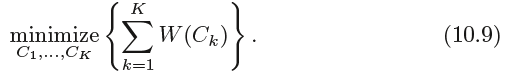
类内差异(W(Ck)):对第Ck类中观测互不相同程度的度量
定义为:

结合10.9和10.10,K-means聚类的最优化问题可以定义为:




