20162321-王彪-程序设计与数据结构-第九周学习总结

堆和优先队列

学习目标

• 定义堆并讨论它的特殊用途
• 讨论堆的链式实现方式
• 讨论堆排序
• 定义优先队列和它与堆的关系

堆

1.堆和二叉查找树

• 堆是一棵完全二叉树，其每个元素都要小于或大于他所有的孩子，若每个元素都大于它的孩子则称之为最大堆，若都小于它的孩子则称之为最小堆。
• 二叉查找树是一棵二叉树，对于其中的每个结点，左子树上的元素小于父结点的值，而右子树上的元素大于等于父结点的值。

2.堆的基本操作

• 向堆中添加一个元素

策略：
（一）将元素添加为新的叶节点，同时保持树是完全树。
（二）将该元素向根的方向移动，将它与父结点对换，直到其中的元素关系满足要求为止。

• 书中以最大堆为例，图例为最小堆
  

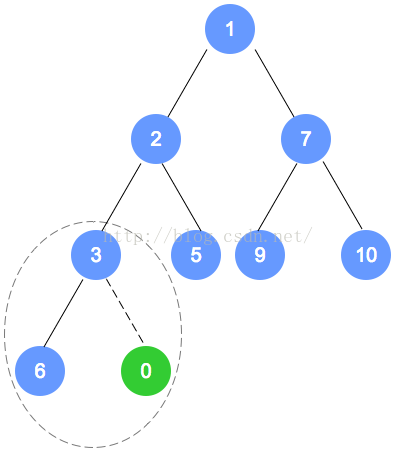
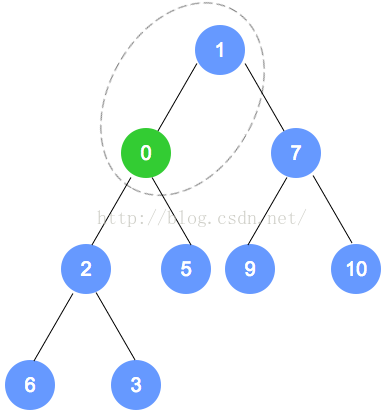
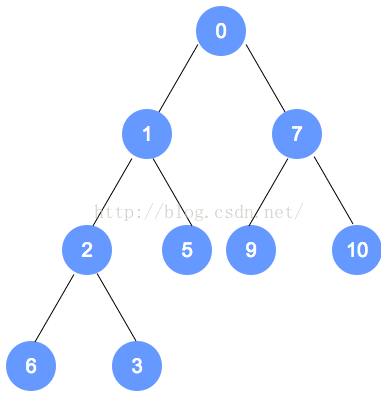
• 从堆中删除最大值元素

策略：
（一）删除树的“最后”的叶节点（最后一层最右边的叶节点），将其放置的到根上。
（二）然后将它在树中下移至满足元素关系的位置。（类似在树中添加新元素的逆过程）
（三）将新根元素与他的孩子进行比较，从而判定它是否需要向下移动（如果根元素小于它的较大孩子，则交换它们。继续此过程，知道两个孩子都小于等于这个元素时为止）

• 书中以最大堆，为例，图例为最小堆
  

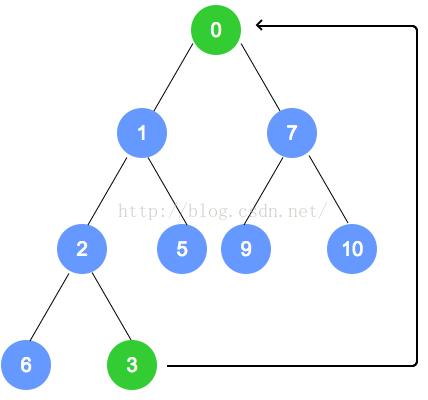
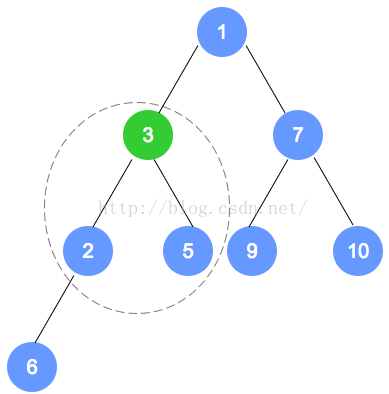
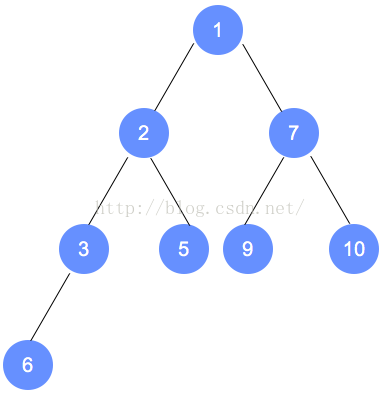
3.堆的实现

• 使用链式结点实现堆

接口：MaxHeap
继承父接口：BinaryTree
所含方法：添加一个新元素，获取最大值，删除最大值
类：LinkedMaxHeap
继承父类：LinkedBinaryTree，实现接口：MaxHeap

• 方法分析及完善

LinkedMaxHeap中的add方法依赖于HeapNode中的两个支撑方法：

• getParentAdd

public HeapNode<T> getParentAdd (HeapNode<T> last)
   {
      HeapNode<T> result = last;
      while ((result.parent != null) && (result.parent.left != result))
         result = result.parent;
      if (result.parent != null)
         if (result.parent.right == null)
            result = result.parent;
         else
         {
            result = (HeapNode<T>) result.parent.right;
            while (result.left != null)
               result = (HeapNode<T>) result.left;
         }
      else
         while (result.left != null)
            result = (HeapNode<T>) result.left;
      return result;
   }

该方法得到要插入的新结点的父结点。从树中的最后一个结点开始，一个结点一个结点地检测，寻找新加入结点的父结点。

• （一）在书中向上进行查找，直到发现它是某个结点的左子结点，或是达到根结点时为止。

• （二）如果达到根结点，则新的父结点是根的最左后继结点。

• （三）如果没有达到根结点，则再查找右子结点的最左后继。

• heapifyAdd

public void heapifyAdd (HeapNode<T> last)
   {
      T temp;
      HeapNode<T> current = last;
      while ((current.parent != null) &&
         ((current.element).compareTo(current.parent.element) > 0))
      {
         temp = current.element;
         current.element = current.parent.element;
         current.parent.element = temp;
         current = current.parent;
      }
   }

该方法的作用是在叶结点插入后重建堆，该过程与向堆中插入新元素的过程是一致的。一旦新的叶节点添加到树中，heapifyAdd方法就利用parent引用沿树向上移动。

优先队列

• “队列”，表明本质上它是一个队列，数据只能在一端进入，另一端出来，但是它强调了“优先”二字，所以，已经不能算是一般意义上的队列了，它的“优先”意指取队首元素时，有一定的选择性，即根据元素的属性选择某一项值最优的出队。

优先队列是0个或多个元素的集合,每个元素都有一个优先权或值,对优先队列执行的操作有1:查找;2: 插入一个新元素;3: 删除.在最小优先队列中,查找操作用来搜索优先权最小的元素,删除操作用来删除该元素;对于最大优先队列,查找操作用来搜索优先权最大的元素,删除操作用来删除该元素.优先权队列中的元素可以有相同的优先权,查找与删除操作可根据任意优先权进行.。要比较优先级，可能就会用到CompareTo方法乐。

堆的实现方法补充

堆的计算链式实现策略

• 代码还未成型

堆的存储链式实现策略

• 代码还未成型

自主堆排序

• 代码还未成型