矩阵一些概念

矩阵

一般矩阵用二维数组表示。常用如3阶和4阶矩阵。

矩阵的乘法：

公式2.1：

A*B=C 

公式2.2：

矩阵的乘法不满足交互率

公式3.1：

A*B ≠ B*A

矩阵乘法得满足一些条(图1)：

 

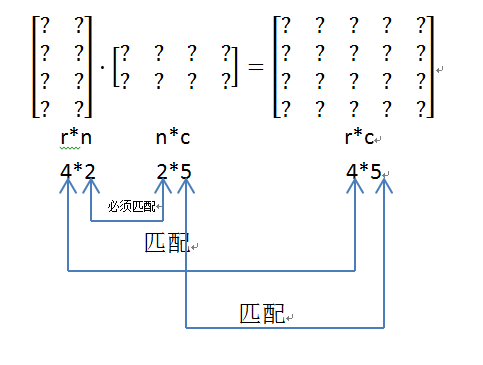
向量和矩阵相乘：

向量如果可以认为是一个行矩阵或者列矩阵

行矩阵：

列矩阵

那样他也满足一般矩阵的乘法公式(2.2)和条件(图1)

一般书籍有两种表达方式 行向量左乘矩阵或者列向量右乘矩阵。

后面的文章默认使用行向量左乘矩阵，其他如行向量右乘矩阵，列向量左乘矩阵都是无意义的。

几何解释：

在2维空间 用两个向量加法表示向量的转换或者说是移动

任意一个向量都可以用分析为其他两个向量的相加

向量在几何上的解析可以认为是一系列在与轴平行的位移。向量的每个单位都表明平行与坐标轴的位移。

同理在三维向量也是

另一种写法，右边都是单位向量

 

我们 P Q R 表示指向+X +Y +Z

 

最终写成

 

这样我们就认为V向量是 向量P Q R 的线性组合，P Q R称作为基向量。

这里的基向量是笛卡尔坐标轴。实际中，我们的坐标系的三个轴可以用任意三个向量，这三个向量要线性无关（就是三个向量不能在同个平面上）

那么我就可以定义矩阵

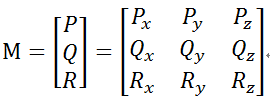
 那么其实矩阵说白了 就是一种非常紧凑的向量表达方式。

我们可以测试下是否正确，任意取一个行向量右乘矩阵

发现两个等式是一样的。说明了 矩阵其实就是向量的线性组合。

 

先写一些旋转公式，后面继续说明一些概念。

简单的三轴旋转公式 ，首先我设置旋转的正负。

我们用左手坐标系，大拇指指向旋转轴与旋转轴平行，四指半握，认为顺着四值的握的方向为正。

绕X轴旋转公式：

绕X旋转时候，Y轴和Z轴变化，X轴不变。

旋转后的X'轴

旋转后的Y‘轴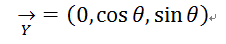

旋转后的Z'轴

根据三个基向量重新构造矩阵

绕Y轴和Z轴旋转也是类似的。

后面的得到旋转矩阵

 

缩放：

在2D向量中，我们用标量K乘上向量表示向量的缩放

可见其实是k值乘上向量的每个基向量，后面用矩阵表示。同理我们可以推理出3维向量中缩放矩阵

如果只是对某个基向量方向做缩放，只要对某个基向量做缩放就可以。

 

齐次坐标W：

在三维空间的变换为什么要用到齐次坐标，矩阵的性质决定任何零向量乘矩阵还是零向量

所以任何三阶矩阵都不包含平移功能。所以出现了齐次坐标w，任何3D坐标表示为

矩阵拓展为四阶矩阵

引入的w就是齐次坐标。

几何解释：

我们可以退化到2D向量去更好的理解齐次。在2D向量和二阶矩阵相乘也是无法进行评议。

我们可以认为向量(x,y,w)是在3D空间一个w的平面上(x,y,w)的一个点。投影到在w这个平面上实际的点

是(x/w,y/w,1);

同理我们在3d向量也加入齐次坐标(x,y,z,w);他在3D空间中实际点的投影是(x/w,y/w,z/w,1);

一般我们把齐次坐标w设置为1,三维向量的表示就是(x,y,z,1);如果w为0，(x,y,z,0)。

我们一般认为这个指向无穷远的方向不是一个点。在4维空间的(x,y,z,k)是一条穿越齐次原点的直线。

 

我们实际使用下四阶矩阵看下跟三阶矩阵的不同。我构造四阶矩阵

 

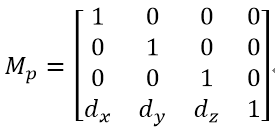
乘上一个向量P

 

各种矩阵性质

 

如果矩阵正交

他转置矩阵跟逆矩阵相等。