软工第2次作业-四则运算器
Github项目地址
https://github.com/wapleeeeee/Arithmetic-operation
PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 10 | 8 |
| · Estimate | · 估计这个任务需要多少时间 | 10 | 8 |
| Development | 开发 | 655 | 785 |
| · Analysis | · 需求分析 (包括学习新技术) | 30 | 35 |
| · Design Spec | · 生成设计文档 | 30 | 40 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 10 | 15 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 5 | 5 |
| · Design | · 具体设计 | 40 | 60 |
| · Coding | · 具体编码 | 5h*60 | 7h*60 |
| · Code Review | · 代码复审 | 1h*60 | 1.5h*60 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 3h*60 | 2h*60 |
| Reporting | 报告 | 290 | 330 |
| · Test Report | · 测试报告+博客 | 4h*60 | 4.5h*60 |
| · Size Measurement | · 计算工作量 | 10 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 40 | 50 |
| 合计 | 955 | 1123 |
项目要求
- √ 参与运算的操作数(operands)除了100以内的整数以外,还要支持真分数的四则运算。操作数必须随机生成。
- √ 运算符(operators)为 +, −, ×, ÷ 运算符的种类和顺序必须随机生成。
- √ 要求能处理用户的输入,并判断对错,打分统计正确率。
- √ 使用 -n 参数控制生成题目的个数。
附加要求
- √ 支持带括号的多元复合运算
- √ 运算符个数随机生成(考虑小学生运算复杂度,范围在2~10)
解题思路
这个题目最开始是在课堂上何老师提出引起大家的思考,一开始我并没有意识到这个题目的复杂性。这个题目可以被划分为以下三个问题:
- 列出随机的四则运算表达式。
- 计算所列出四则运算的结果。
- 接受用户输入并比较结果是否正确,并在命令行中表现出来。
如何解决
问题1
- 随机操作数、随机运算符、随机括号、随机长度等随机变量可以利用python自带随机函数取得。
- 需要考虑除数及分母为0时的情况,此时表达式不成立。
- 需要考虑随机生成括号的位置是否有意义的情况。例如:
expression: (1+2+5)-(3*4)=
问题2
求一般四则算数表达式的结果一般采用转化为逆波兰表达式。
该种方法一般思路为:
- 将中缀表达式转化成后缀表达式。
- 通过栈计算后缀表达式的值。
其中需要考虑运算符优先级问题以及栈的结构。查阅了网上的资料,参考了dragondove的博客以及yichudu的博客。其中都有关于该算法的的具体描述。
问题3
判断用户输入情况只需接受用户输入比较统计得分即可。由于要求采用命令行界面完成,该部分主要需要控制及美化命令行界面。
测试部分
由于四则运算的规则繁杂,随机生成的算式需要判断各种情况的产生,也就无形之中给测试部分增添了很大压力。看过了《构建之法》第二章的所有测试部分之后,利用其中单元测试的部分对项目进行了统一的测试。详细情况见后文测试部分。
设计实现
一、总体设计
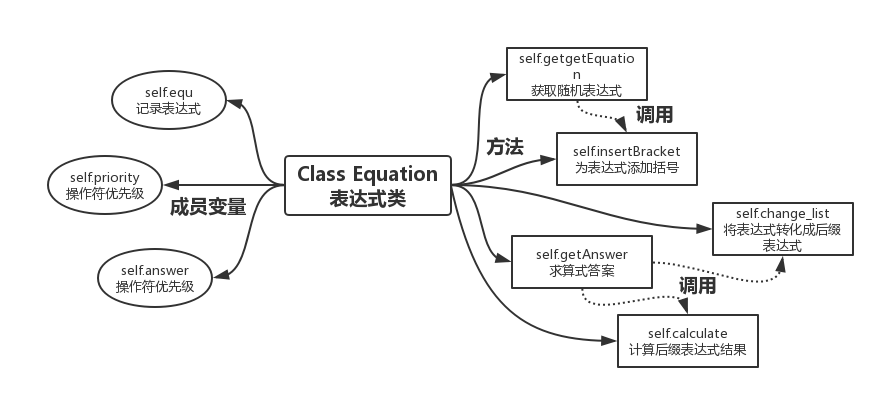
二、具体程序设计
主程序main()用于处理命令行输入输出,建立了一个类Equation用于保存每一个表达式的属性。以下为类中成员变量及成员方法具体介绍。
成员变量
| 变量名 | 类型 | 功能 |
|---|---|---|
| equ | string | 由随机产生运算符的函数保存生成的表达式。 |
| priority | dict | 存放运算符优先级的字典,用于比较优先级大小。 |
| answer | Fraction | 保存最终得到的表达式结果 |
| op | list | 运算符库 |
成员函数
| 函数名 | 输入 | 输出 | 依赖函数 | 功能 |
|---|---|---|---|---|
| getEquation | void | string finalstring:表达式函数 | insertBracket | 生成随机表达式,需要调用随机添加括号函数 |
| insertBracket | string equ:表达式 | string tmplist:表达式函数 | void | 在原表达式基础上随机添加括号 |
| getAnswer | string equ:表达式 | Fraction answer:计算结果 | change_list calculate | 根据表达式计算结果 |
| change_list | list 中缀表达式 | list 后缀表达式 | void | 将中缀表达式转化为后缀表达式 |
| calculate | list 后缀表达式 | Fraction answer:计算结果 | void | 根据后缀表达式计算结果 |
代码说明
核心函数为getEquation(生成随机表达式)和getAnswer(计算结果)
#生成随机等式
def getEquation(self):
number = random.randint(2,9)
tmpstring = ""
tmpop = ''
tmpint = 0
for i in range(number):
if tmpop == '/': #分数情况
tmpint = random.randint(tmpint+1,9)
tmpop = random.choice(self.op[:-1])
elif tmpop == '÷': #除号情况
tmpint = random.randint(1,8)
tmpop = random.choice(self.op)
else:
tmpint = random.randint(0,8)
tmpop = random.choice(self.op)
#添加到算式中
tmpstring += str(tmpint)
tmpstring += tmpop
tmpstring = list(tmpstring)
#修改最后一个符号为=
tmpstring[-1] = '='
tmpstring = ''.join(tmpstring)
#加括号
finalstring = self.insertBracket(tmpstring,number)
return finalstring
#求算式答案
def getAnswer(self,exp):
#将带有分号的表达式化成带分数的list
equlist = []
i = 0
while(i < len(exp)-1):
if exp[i+1] != '/':
equlist.append(exp[i])
i += 1
else:
equlist.append(Fraction(int(exp[i]),int(exp[i+2])))
i += 3
#将中缀表达式转化为后缀
new_equlist = self.change_list(equlist)
#计算后缀表达式的结果
return(self.calculate(new_equlist))
运行效果
运行结果如下所示:
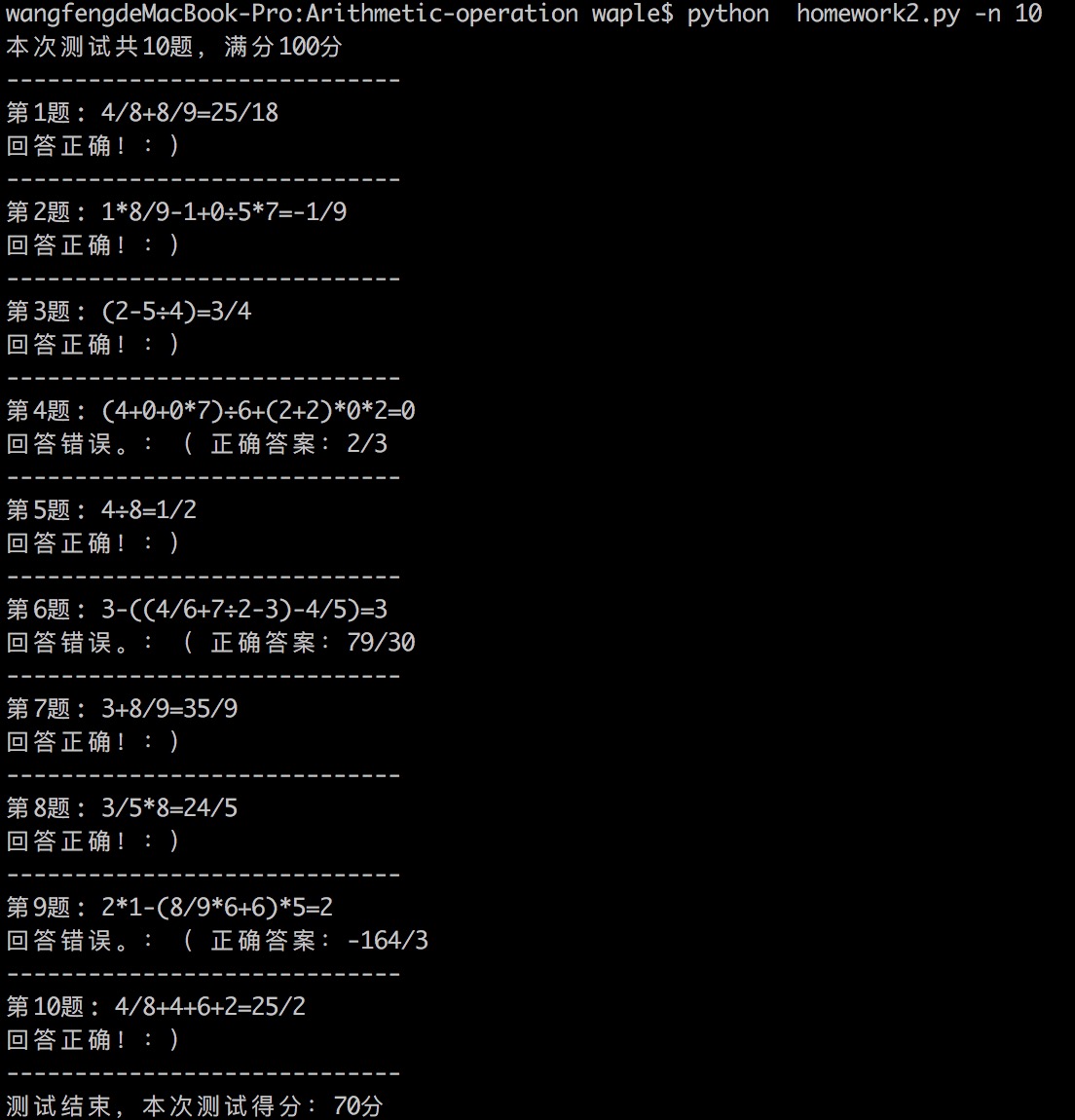
单元测试
《构建之法》第二章中详细提及了好的单元测试的标准。
- 单元测试应该在最基本的功能/参数上检验程序的正确性。
- 单元测试必须由最熟悉代码的人来写。
- 单元测试过后,机器状态保持不变。
- 单元测试要快。
- 单元测试应该产生可重复、一致的结果。
- 独立性-单元测试的运行/通过/失败不依赖于别的测试,可以人为构造数据,以保持测试的独立性。
- 单元测试应该覆盖所有代码路径。
这些思想再加上该项目中表达式内容和形式的千变万化,构建出一套合适的测试体系成为了这个项目中不可或缺的重要部分。因此我对表达式类中每一个函数详细地构造出一套测试方法。
| 函数名 | 输入 | 输出 | 测试方法 | 备注 |
|---|---|---|---|---|
| getEquation | void | string finalstring:表达式函数 | 使用python自带eval函数检验式子合法性 | 由于该函数包含insertBracket并且输出相同,只需要测试该函数即可覆盖。 |
| getAnswer | string equ:表达式 | Fraction answer:计算结果 | 给出不同情况的表达式,测试输入输出结果是否相同。 | |
| change_list | list 中缀表达式 | list 后缀表达式 | 给出特定中缀表达式,测试能否转化成所期待的后缀表达式。 | 包含于getAnswer,但需要单独测试。 |
| calculate | list 后缀表达式 | Fraction answer:计算结果 | 输入指定后缀表达式,匹配结果是否相同。 | 包含于getAnswer,但需要单独测试。 |
getEquation函数
测试代码如下:
#对getEquation函数测试
def test_getEquation(self):
#随机1000000次
for i in range(1000000):
tmpString = self.equation.getEquation()[:-1] #保存生成的算式
tmpString.replace('÷','/') #将无法识别的除号替换
self.assertEqual(type(tmpString),(str or int))
测试了100W次随机生成的字符串,用时30.418s。

- √ 通过测试
getAnswer函数
getAnswer需要输入一个确定的表达式,输出表达式的结果,选取了十组测试用例如下(Fraction(a,b)表示a/b):
| 输入表达式 | 期待返回值 |
|---|---|
| "(1+2)*3=" | 9 |
| "(6+4/5)÷3=" | Fraction(34,15) |
| "(8/9-7-2+3)+3*4-2/9=" | Fraction(20,3) |
| "3*7-3-6+3=" | 15 |
| "5+5/9+6-5÷(6/8+3/6)=" | Fraction(68,9) |
| "1-6=" | -5 |
| "3÷1+8÷5*4*5-2/9*2=" | Fraction(311,9) |
| "(5+(6-3)*3/5)÷7=" | Fraction(34,35) |
| "(1+2)*(3*(4+5))=" | 81 |
| "4+6*0=" | 4 |
| 单独运行测试得到结果如下: | |
 |
change_list函数
change_list函数需要输入一个中缀表达式列表,返回一个后缀表达式列表,同时将列表中字符串类型的数字转化为可运算的整型。
| 输入中缀列表 | 期待返回列表 |
|---|---|
| ["1", "+", Fraction(2,3), "÷", "3"] | [1, Fraction(2,3), 3, "÷", "+"] |
| ['4', '*', '0', '*', '5', '÷', '7', '-', '0', '÷', '3'] | [4, 0, '*', 5, '*', 7, '÷', 0, 3, '÷', '-'] |
| ['2', '-', '6', '+', '4', '+', Fraction(1, 4), '÷', '5', '-', '5'] | [2, 6, '-', 4, '+', Fraction(1, 4), 5, '÷', '+', 5, '-'] |
| ['6', '*', '7'] | [6, 7, '*'] |
| ['7', '*', '(', '0', '÷', '4', '-', '5', ')'] | [7, 0, 4, '÷', 5, '-', '*'] |
| ['0', '*', '7', '+', '(', '8', '+', '7', '*', '6', ')', '÷', '4', '*', '4', '-', '7', '-', '4'] | [0, 7, '*', 8, 7, 6, '*', '+', 4, '÷', 4, '*', '+', 7, '-', 4, '-'] |
| ['0', '+', '1', '*', '8', '÷', '8', '*', '7'] | [0, 1, 8, '*', 8, '÷', 7, '*', '+'] |
| [Fraction(3, 7), '÷', '3', '÷', Fraction(2, 3), '÷', '3'] | [Fraction(3, 7), 3, '÷', Fraction(2, 3), '÷', 3, '÷'] |
| [Fraction(6, 7), '+', '0', '*', '(', '6', '-', '(', '3', '-', Fraction(5, 8), ')', ')'] | [Fraction(6, 7), 0, 6, 3, Fraction(5, 8), '-', '-', '*', '+'] |
| ['(', '4', '+', '8', '-', '4', '-', '3', '+', '2', '*', '0', ')', '÷', '4'] | [4, 8, '+', 4, '-', 3, '-', 2, 0, '*', '+', 4, '÷'] |
| 运行结果如下: | |
 |
calculate函数
calculate函数是输入一个正确的后缀表达式,根据这个输入得到确定结果的方法,由于该方法的分支并不多,所以只选取五组测试用例。
| 输入后缀列表 | 期待返回值 |
|---|---|
| [6, Fraction(2, 5), '÷', 2, 3, '÷', '-', 1, 4, '*', '-'] | Fraction(31,3) |
| [0, 3, 7, '÷', 6, '÷', 0, '-', '÷', 7, '÷'] | 0 |
| [Fraction(8, 9), Fraction(2, 3), '+', 5, 5, '÷', 5, 1, '-', '÷', 7, '*', '+'] | Fraction(119,36) |
| [4, 7, 1, '+', Fraction(8, 9), '+', '*', 5, 6, '÷', '-'] | Fraction(625,18) |
| [2, 1, '÷', 8, '÷', 8, '*', Fraction(1, 2), '÷', Fraction(5, 8), '÷'] | Fraction(32,5) |
| 单元测试运行效果如下: | |
 |
集成测试
将以上五个单元测试叠在一起测试,并且增加了错误情况的判断,让方法鲁棒性更强。测试结果如下:

效能分析与改进
首先考虑到用户输入会影响效能分析中的时间因素,去掉了主函数中接受用户输入并比较的部分,直接改成由代码随机生成算式然后计算结果。
python中的效能分析工具这是一个非常好用的python性能分析工具的介绍,包含了line_profiler(时间分析)以及memory_profiler(内存分析)等python包。
开始
首先测试10W条
统计出五个函数的运行时间及细节如下:
getEquation函数
10W次运行时间15.3507s(33.73%)
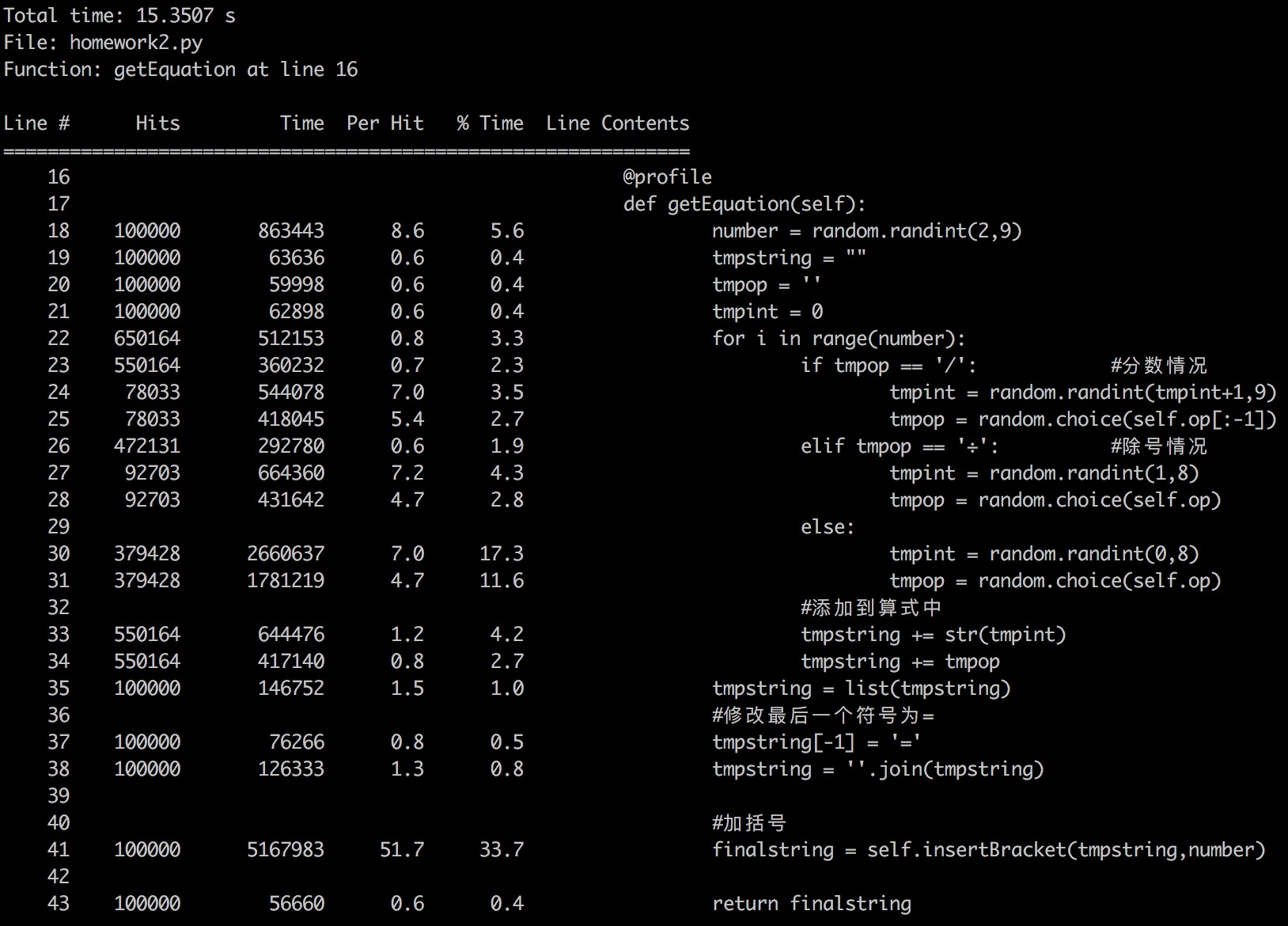
insertBracket函数
10W次运行时间3.30584s(9.26%)
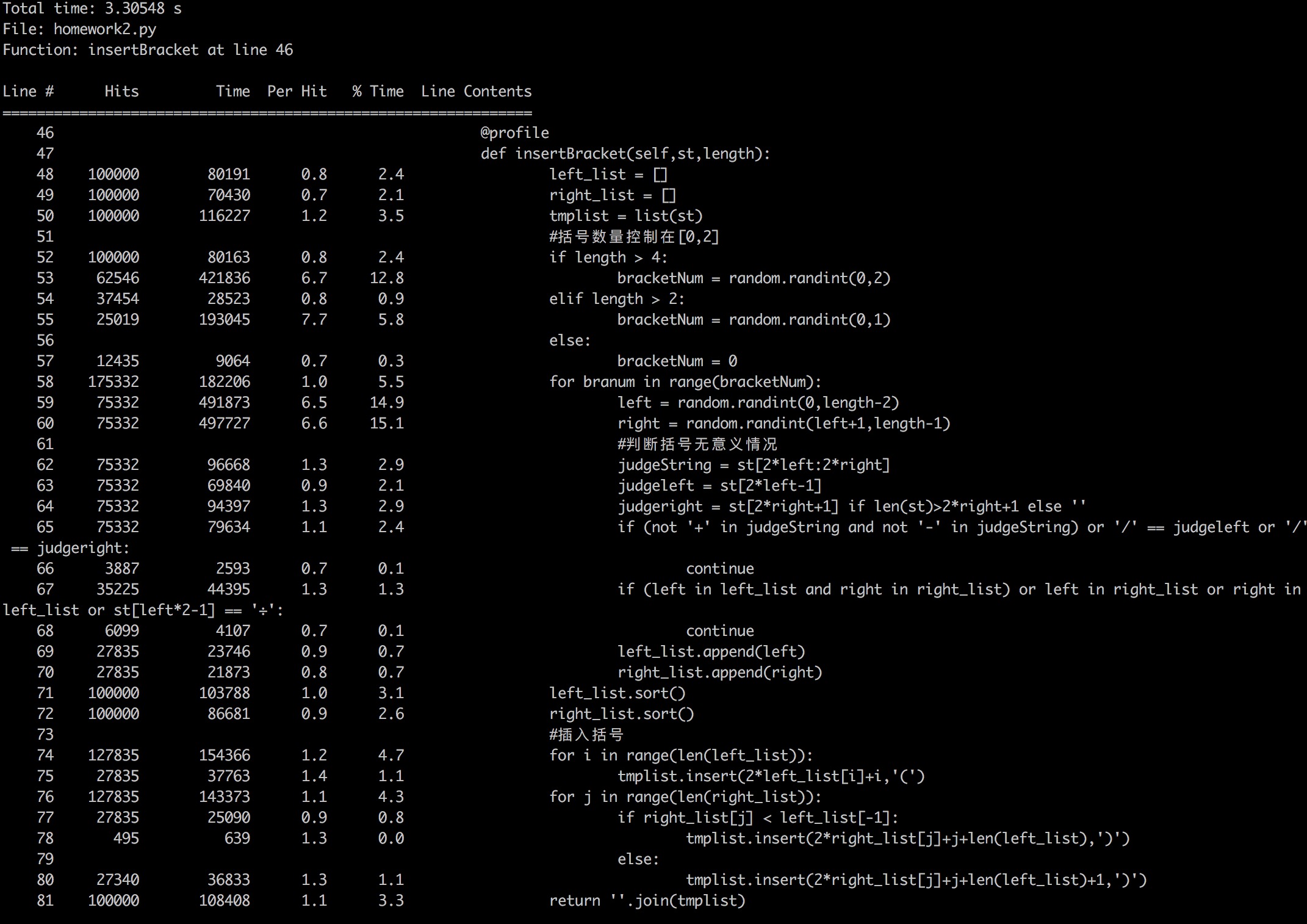
getAnswer函数
10W次运行时间20.3809s(25.7%)(函数内)
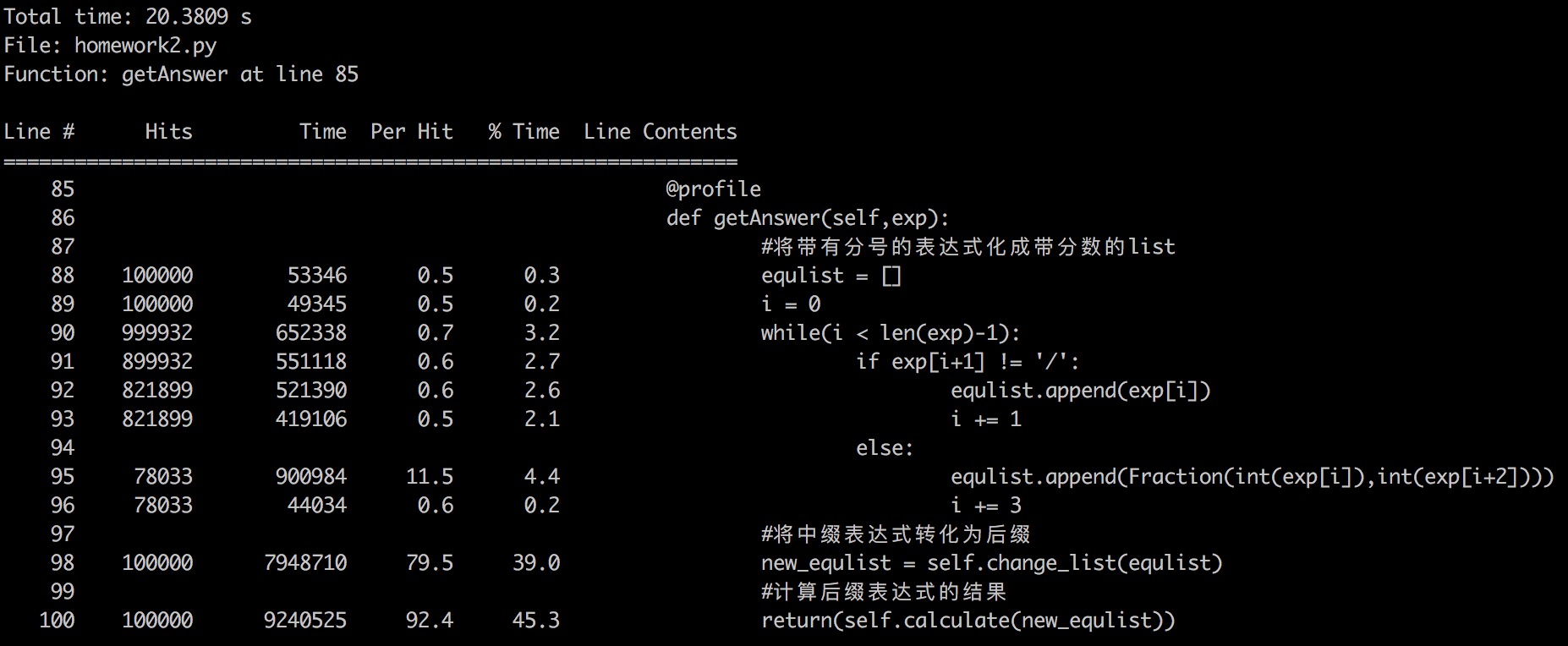
change_list函数
10W次运行时间4.4608s(12.68%)
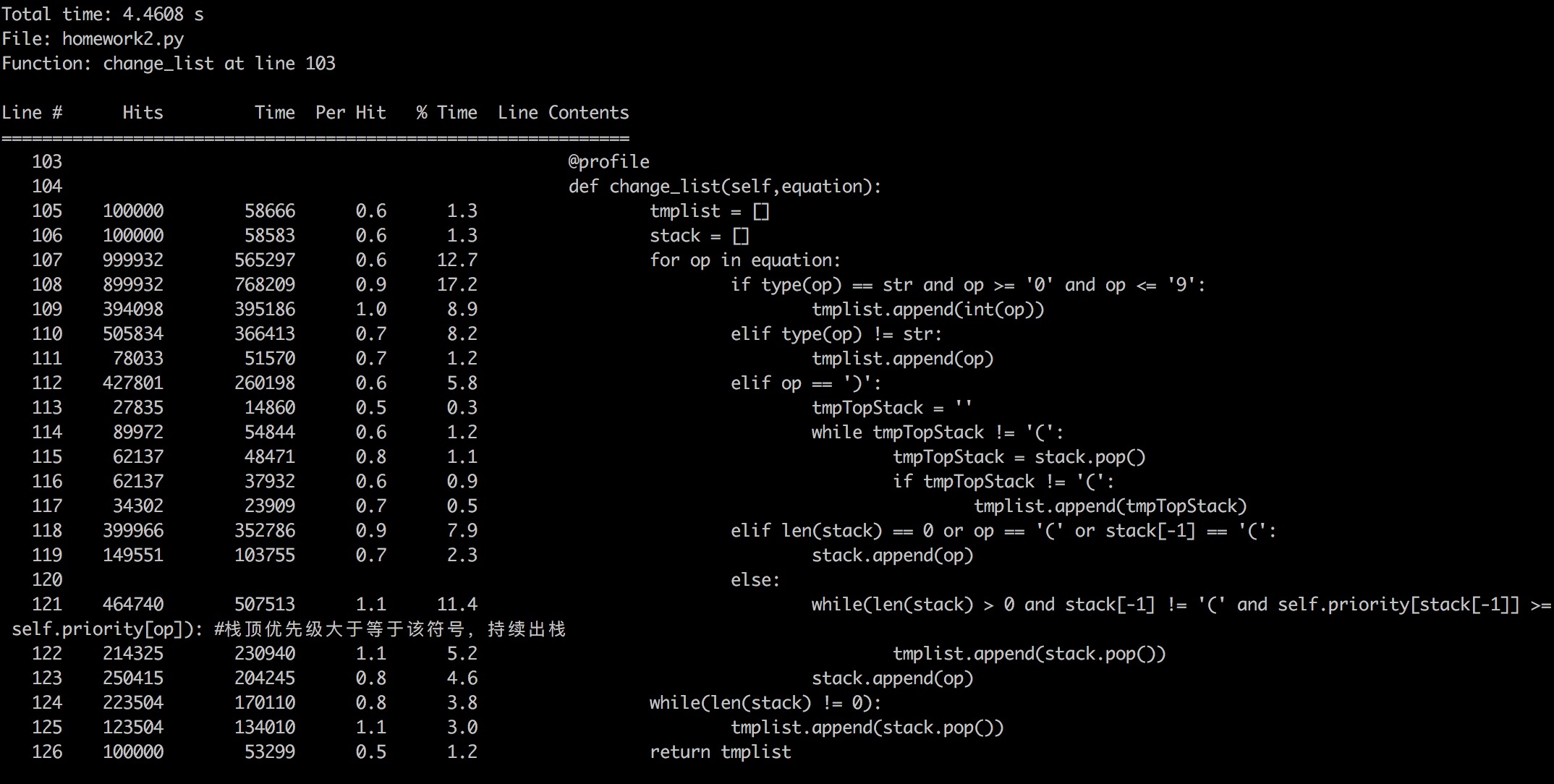
calculate函数
10W次运行时间6.73093s(18.85%)
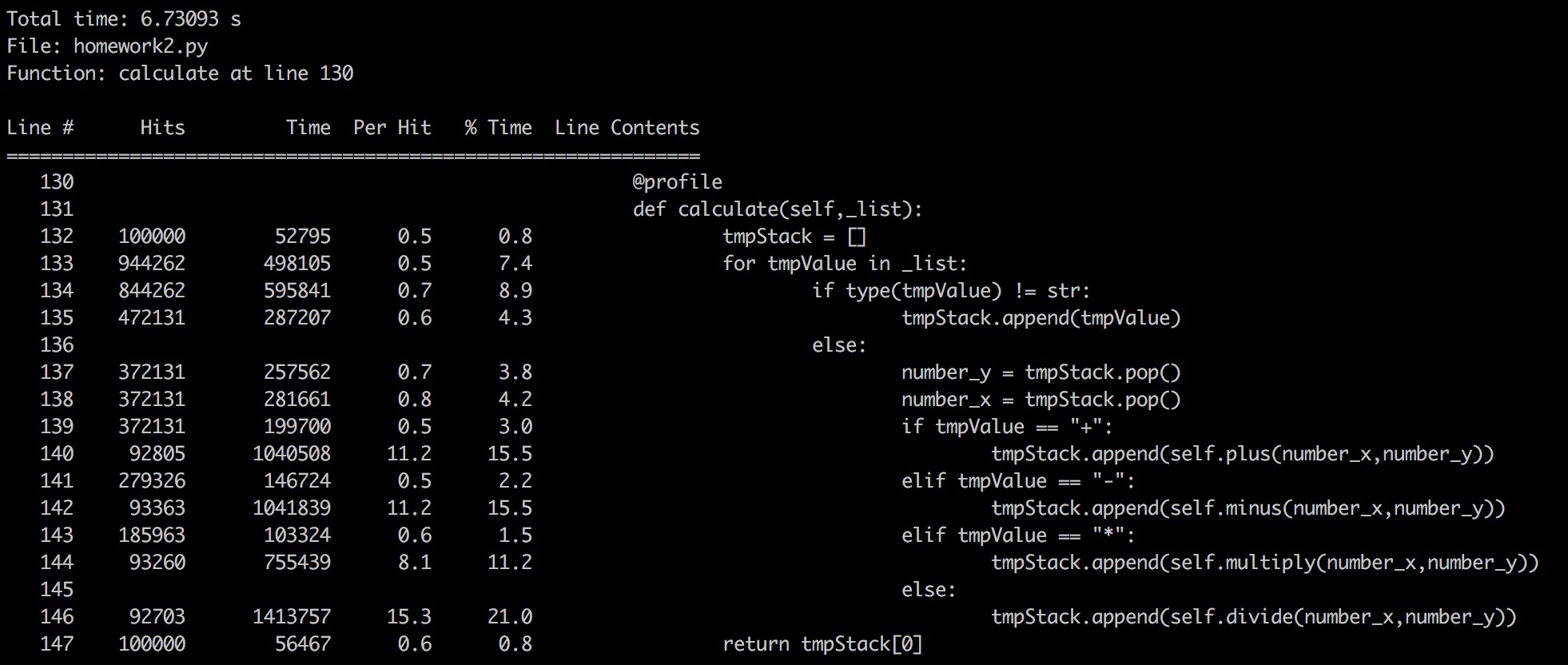
共计耗时35.7136s。
分析perhit参数(平均每次调用产生的时间)可以很快速地找到哪些语句占用了程序的大多数时间。
抽取了其中部分perhit较高的参数如下表:
| 出现函数 | 代码句 | Per Hit |
|---|---|---|
| getEquation | number = random.randint(2,9) | 8.6 |
| getEquation | tmpint = random.randint(tmpint+1,9) | 7.0 |
| insertBracket | bracketNum = random.randint(0,1) | 7.7 |
| insertBracket | right = random.randint(left+1,length-1) | 6.6 |
| getAnswer | equlist.append(Fraction(int(exp[i]),int(exp[i+2]))) | 11.5 |
| calculate | tmpStack.append(self.plus(number_x,number_y)) | 15.5 |
| calculate | tmpStack.append(self.minus(number_x,number_y)) | 15.5 |
| calculate | tmpStack.append(self.multiply(number_x,number_y)) | 11.2 |
| calculate | tmpStack.append(self.divide(number_x,number_y)) | 21.0 |
分析上表可以看出,效率不高的几条语句大致可以分为以下三类:
- 调用random.randint得到随机值。
- 一条参数中使用很多方法嵌套。
- 调用类中的其他函数。
改进
- python中random.randint是一个产生随机数的高效方法,本身没有多少能够替换的函数。由于我们只需要random中的randint函数,于是考虑替换import方式:
import random -> from random import randint
- 多方法嵌套本身需要完成的任务较多,实际上对效率并没有太大影响。
- 计算表达式中原来列出了四个加减乘除的运算函数,但除了这里调用了之外并没有其他地方调用,这里可能才是优化的重点部分。
tmpStack.append(self.plus(number_x,number_y)) -> tmpStack.append(number_x + number_y)
tmpStack.append(self.plus(number_x,number_y)) -> tmpStack.append(number_x - number_y)
tmpStack.append(self.plus(number_x,number_y)) -> tmpStack.append(number_x * number_y)
tmpStack.append(self.plus(number_x,number_y)) -> tmpStack.append(Fraction(number_x,number_y))
做了以上工作后重新跑了10W次后。
运行时间为15.0372s+19.3621s=34.3993s
仅仅只快了1s不到。。
回头看看randint优化的百分比并不多,不考虑在这个上面做文章了。
再看刚刚修改的函数调用部分,虽然提高了不少,但跟其他语句比起来依然惨淡不少:

进一步分析发现每一句话都调用了tmpStack.append(x),于是考虑改变结构:
if tmpValue == "+":
tmp = number_x+number_y
elif tmpValue == "-":
tmp = number_x-number_y
elif tmpValue == "*":
tmp = number_x*number_y
else:
tmp = Fraction(number_x,number_y)
tmpStack.append(tmp)
再次运行10W次,这次缩短到了13.5085s+17.9572s=31.4657s
运行效率增长了13.50%,虽然跟范文数独博客中的1000%小哥比起来相差甚远,不过考虑到四则运算需要考虑的情况之多以及功能的复杂性,在时间上没有更大的优化的空间了。
总结及收获
本次项目虽然核心算法要求并不难,但是包括测试优化自身调整以及写好总结博客这一整套开发我还是第一次这么完整地做下来。过程也可谓是坎坷不断。但这也正反映了《构建之法》实践这一节中对“软件工程”作业的要求:
软件工程的作业,不仅仅是程序,而是要加入软件工程的要素(复杂性、易变性和其他),有价值的软件工程的作业必须要触及这两个基本要素!
无论是从测试内容的丰富性还是效能测试的复杂性来讲,这一次作业都让我从实际动手应用中收获了不少“软件开发流程”相关知识。
在效能测试模块,为了让代码的运行效率提高到理想值(100%),基本把每一条语句都尝试修改成“更好的形式”,但是结果并不尽如人意,有的只是提升了微乎其微的零点几秒,有的甚至让运行时间负增长。最后得到的13.5%的提高虽然不是很好看,但是也心服口服。
当然无论是从算法到测试再到效能提升,肯定还是有很多改进空间的,以后发现了再补充。
未完待续...



