深度学习中常见的几个基础概念
深度学习中常见的几个基础概念
1. Linear regression :
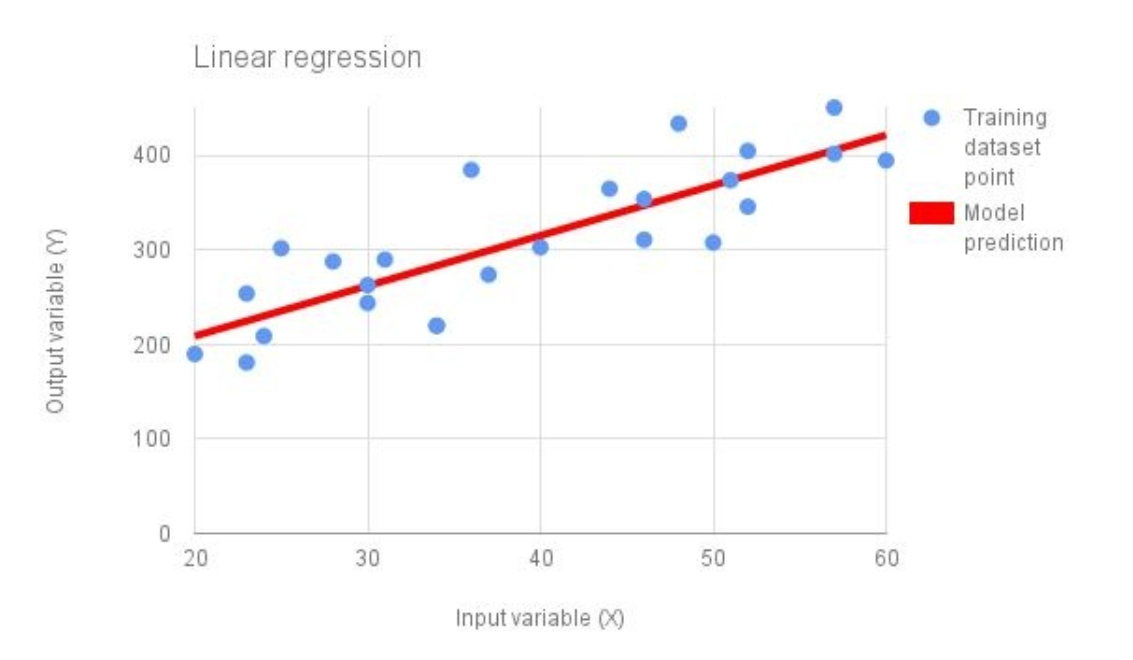
Linear regression 对监督学习问题来说, 是最简单的建模形式. 上图蓝色点表示 training data point, 红色的线表示用于拟合训练数据的线性函数. 线性函数的总的形式为:

在代码中表示这个模型, 可以将其定义为 单列的向量 (a single column vector) :
# initialize variable / model parameters.
w = tf.Variable(tf.zeros([2, 1]), name = "weights")
b = tf.Variable(0., name = "bias")
def inference(X):
return tf.matmul(X, W) + b
既然我们已经定义了如果计算 loss , 此处 loss 函数我们设置为 squared error.
$ loss = \sum_{i} (y_i - y_{predicted_i})^2 $
我们统计 i, i 是每一个数据样本. 代码上表示为:
def loss (X, Y) :
Y_predicted = inference(X)
return tf.reduce_sum(tf.squared_difference(Y, Y_predicted))
def inputs():
weight_age = [[84, 46], [73, 20], [65, 52], [70, 30], [76, 57], [69, 25], [63, 28], [72, 36], [79
blood_fat_content = [354, 190, 405, 263, 451, 302, 288, 385, 402, 365, 209, 290, 346, 254, 395,
return tf.to_float(weight_age), tf.to_float(blood_fat_content)
我们利用 gradient descent 算法来优化模型的参数 :
def train(tota_loss) :
learning_rate = 0.000001
return tf.train.GradientDescentOptimizer (learning_rate).minimize(total_loss)
当你运行之后, 你会发现随着训练步骤的进行, 展示的 loss 会逐渐的降低.
def evaluate(sess, X, Y):
print sess.run(inference([[80., 25.]])) # ~ 303
print sess.run(inference([[65., 25.]])) # ~ 256
Logistic regression.
线性回归模型预测的是一个连续的数字 (continuous value) , 或者其他任何 real number. 我们接下来会提供一个可以回答 yes-or-no 问题的模型, 例如 : " Is this email spam ? "
有一个在机器学习领域被常用的一个模型, 称为: logistic function. 也被称为 sigmoid function, 形状像 S .
$ f(x) = 1/(1+e^{-x}) $

这里你看到了一个 logistic / sigmoid function 的图, 像 "S" 形状.
这个函数将 single input value 作为输入. 为了给这个函数输入多维, 或者我们训练数据集样本的特征 , 我们需要将他们组合为一个 value. 我们可以利用 线性回归模型 来做这个事情 .
# same params and variable initialization as log reg.
w = tf.Variable(tf.zeros([5, 1]), name = "weights")
b = tf.Variable(0., name = "bias")
# former inference is now used for combing inputs.
def combine_inputs(X) :
return tf.matmul(X, W) + b
# new inferred value is the sigmoid applied to the former.
def inference(X) :
return tf.sigmoid (combine_inputs(X))
这种问题 交叉熵损失函数解决的比较好.
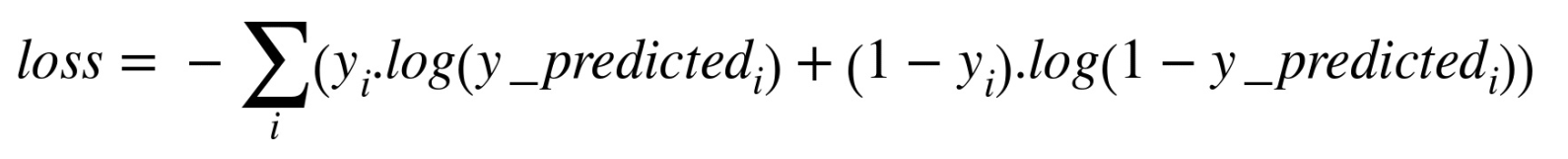
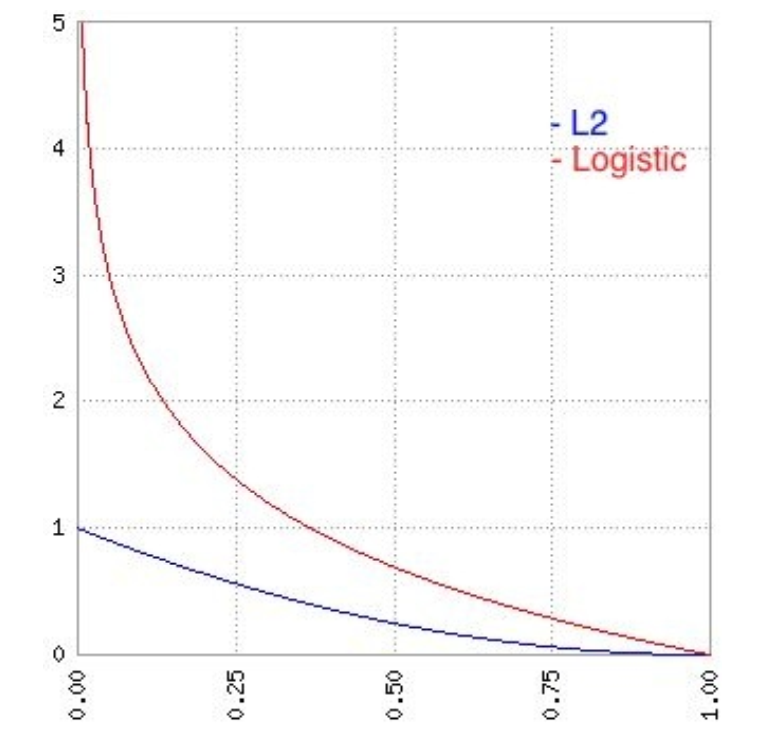
我们可以视觉上比较 两个损失函数的表现, 根据预测的输出.
def loss (X, Y) :
return tf.reduce_mean (tf.sigmoid_cross_entropy_with_logits (combine_inputs(X), Y)
What "Cross-entropy" means :
加载数据 :
def read_csv (batch_size, file_name, record_defaults) :
filename_queue = tf.train.string_input_producer([os.path.dirname(__file__) + "/" + file_name])
reader = tf.TextLineReader (skip_header_lines = 1)
key, value = reader.read(filename_queue)
# decode_csv will convert a Tensor from type string (the text line) in
# a tuple of tensor columns with the specified defaults, which also sets the data type for each column .
decoded = tf.decode_csv(value, record_defaults = record_defaults)
# batch actually reads the file and loads "batch_size" rows in a single tensor
return tf.train.shuffle_batch(decoded, batch_size=batch_size, capacity = batch_size * 50, min_after_dequeue = batch_size)
def inputs ():
passenger_id, survived, pclass, name, sex, age, sibsp, parch, ticket, fare, cabin, embarked = \
read_csv (100, "train.csv", [[0.0], [0.0]] ........)
# convert categorical data .
is_first_class = tf.to_float (tf.equal(pclass, [1]))
is_second_class = tf.to_float (tf.equal(pclass, [2]))
is_third_class = tf.to_float (tf.equal (pclass, [3]))
gender = tf.to_float (tf.equal (sex, ["female"]))
# Finally we pack all the features in a single matrix ;
# We then trainspose to have a matrix with one example per row and one feature per column.
features = tf.transpose (tf.pack([is_first_class, is_second_class, is_third_class, gender, age]))
survived = tf.reshape(survived, [100, 1])
return features, survived



