论文笔记之：Progressive Neural Network Google DeepMind
Progressive Neural Network
Google DeepMind
摘要：学习去解决任务的复杂序列 --- 结合 transfer (迁移)，并且避免 catastrophic forgetting （灾难性遗忘） --- 对于达到 human-level intelligence 仍然是一个关键性的难题。本文提出的 progressive networks approach 朝这个方向迈了一大步：他们对 forgetting 免疫，并且可以结合 prior knowledge 。在强化学习任务上做了一系列的实验，超出了常规的 pre-training 和 finetuning 的 baseline。利用一个新颖的 sensitivity measure（感知衡量），我们表明在 low-level sensory 和 high-level control layers 都发生了transfer 。
Introduction ：
利用卷积神经网络（CNN）进行微调是迁移学习的一种方式。Hinton 首次在 2006 年尝试了这种迁移学习的方法，从产生式模型上迁移到判别模型上。 在 2012年 Bengio 也尝试了这种方式，取得了极大的成功，相关文章见：Unsupervised and transfer learning challenge: a deep learning approach. 但是这种方法致命的缺陷在于，不适合进行 multi-task 的迁移 ： if we wish to leverage knowledge acquired over a sequence of experiences, which model should we use to initialize subsequent models? （如果我们希望将一个序列的经验利用上，那么该用什么模型来初始化接下来的序列模型呢？）这样的话，就使得不仅需要一种学习方法，可以支持 transfer learning，并且没有 catastrophic forgetting，并且要求前面的知识必须是类似的。除此之外，当进行 finetuning 的时候，允许我们在 target domain 恢复出顶尖的性能，也是一个毁灭的过程，其将要扔掉之前学习到的函数。当然我们可以显示的在微调之前复制每一个model，来显示的记住所有的之前任务，但是仍然存在选择一个合适的初始化的问题。
本文就在这个motivation的基础上，就提出了一种 progressive networks，一种新颖的模型结构来显示的支持不同任务序列之间进行迁移学习。微调只有在初始化的时候，才会结合先验信息，progressive networks 保留了一个 pool 用来存储训练过程当中 pre-trained model，然后从那些模型中提取有用的特征，学习 lateral connections ，来进行新任务的训练。通过这种方式结合之前学习到的特征，progressive networks 达到了更丰富的 组合性，先验知识不再是端在存在的，而可以在每一层都结合进来，构成 hierarchy feature。此外，预训练网络的新的存储 提供了这些模型灵活的重新利用 old computations 并且学习新的。如我们即将展示的那样，progressive networks 自然的累积了经验，而且对于灾难性遗忘具有免疫能力，通过设计，making them an ideal springboard for trackling long-standing problems of continual or lifelong learning.
本文的创新点在于三个地方：
1. progressive networks 当中的每一个成分都是现有的，但是将其组合，并且用于解决复杂的序列或者任务，这一点是比较 novel的；
2. 我们充分的将该模型在复杂的 RL 领域进行了验证。在这个过程中，我们也验证了在 RL 领域的另一个 transfer 的方式；
3. 特别的，我们表明 progressive networks 提供了comparable 的迁移能力 （if not slightly better）相对于传统的微调来说，但是没有破坏序列（without the destructive consequences）
4. 最后，我们在 Fisher Information and perturbation 基础上进行了新颖的分析，使得我们可以细致的分析，怎么在任务之间进行了迁移（回答了 how and where 的问题）
2 Progressive Networks ：
持续学习 （continual learning）是机器学习领域当中的长远目标，agents 不仅学习 （and remember）一系列的任务经验，同时也有能力去从之前的任务上迁移出有用的知识来改进收敛的速度。
Progressive Networks 将这些急需品 直接结合到框架中：
1. catastrophic forgetting is prevented by instantiating a new neural network (a column) for each task being solved,
2. while transfer is enabled via lateral connections to features of previously learned columns.
3. The scalability of this approach is addressed at the end of this section.
一个 Progressive networks 是由单列的网络开始的：a deep neural network having L layers with hidden activations $h_i^{(1)}$，其中，ni 是第 i 层的单元个数，以及参数 
训练到收敛。
当切换到第二个网络的时候，我们固定住参数 
，并用随机初始化的方式，开始第二个任务，其参数记为 
，layer $h_i^{(2)}$ 从 $h_{i-1}^{(2)}$ and $h_{i-1}^{(1)}$ 两个地方接收到输入，通过 lateral connections。这种连接方式，拓展到 K 个任务的时候，可以记为：
其中， 
是第 k 列 的 第 i 层的权重矩阵， U 是从 第 j 列的 第 i-1 层到 第 k 列的第 i 层 的 lateral connections ， $h_0$ 是网络的输入。
f 是 an element-wise non-linearity: we use f(x) = max(0, x) for all intermediate layers. 一个 Progressive networks 的示意图为：
这些模型所起到的作用有：
(1). 最终达到解决 K 个独立任务的训练 ；
(2). 当可能的时候，通过迁移，加速学习过程；
(3). 避免灾难性遗忘的问题。
在标准的预训练 和 微调机制上，有一个隐含的假设："overlap" between the tasks.
微调是一种这种设置下，特别有效，因为这个时候，参数只要稍微调整一下，就可以适应 target domain，通常 the top layer is retained. 作为对比，我们不假设任务之间存在这种关系，那么实际上，可能任务之间是互相垂直的，或者说是对抗的。当微调阶段可能潜在的不学习这些 features，这可能证明是困难的。Progressive Networks 绕开了这个问题，通过给每一个新的任务，配置一个新的列，其权重随机的初始化。与和任务相关的初始化 预训练相比较，Progressive Networks 的列，是可以随意 reuse，modify or 通过 lateral connections 忽略之前学习到的features。因为 lateral connections U 仅仅从 第 k 列到第 j 列，之前的列，不受前向传播中学习到的特征的影响。因为参数 
是固定的，当训练 
的时候，任务之间并没有相互干扰，所以不存在毁灭性的遗忘。
另外，可以参考这篇博文： https://blog.acolyer.org/2016/10/11/progressive-neural-networks/?utm_source=tuicool&utm_medium=referral
Rusu et al, 2016
If you’ve seen one Atari game you’ve seen them all, or at least once you’ve seen enough of them anyway. When we (humans) learn, we don’t start from scratch with every new task or experience, instead we’re able to build on what we already know. And not just for one new task, but the accumulated knowledge across a whole series of experiences is applied to each new task. Nor do we suddenly forget everything we knew before – just because you learn to drive (for example), that doesn’t mean you suddenly become worse at playing chess. But neural networks don’t work like we do. There seem to be three basic scenarios:
- Training starts with a blank slate
- Training starts from a model that has been pre-trained in a similar domain, and the model is then specialised for the target domain (this can be a good tactic when there is lots of data in the pre-training source domain, and not so much in the target domain). In this scenario, the resulting model becomes specialised for the new target domain, but in the process may forget much of what it knew about the source domain (“catastrophic forgetting”). This scenario is called ‘fine tuning’ by the authors.
- Use pre-trained feature representations (e.g. word vectors) as richer features in some model.
The last case gets closest to knowledge transfer across domains, but can have limited applicability.
This paper introduces progressive networks, a novel model architecture with explicit support for transfer across sequences of tasks. While fine tuning incorporates prior knowledge only at initialization, progressive networks retain a pool of pretrained models throughout training, and learn lateral connections from these to extract useful features for the new task.
The progressive networks idea is actually very easy to understand (somewhat of a relief for someone like myself who is just following along as an interested outsider observing developments in the field!). Some of the key benefits include:
- The ability to incorporate prior knowledge at each layer of the feature hierarchy
- The ability to reuse old computations and learn new ones
- Immunity to catastrophic forgetting
Thus they are a stepping stone towards continual / life-long learning systems.
Here’s how progressive networks work. Start out by training a neural network with some number L of layers to perform the initial task. Call this neural network the initial column of our progressive network:
When it comes time to learn the second task, we add an additional column and freeze the weights in the first column (thus catastrophic forgetting, or indeed any kind of forgetting is impossible by design). The outputs of layerl in the original network becomes additional inputs to layer l+1 in the new column.
The new column is initialized with random weights.
We make no assumptions about the relationship between tasks, which may in practice be orthogonal or even adversarial. While the fine tuning stage could potentially unlearn these features, this may prove difficult. Progressive networks side-step this issue by allocating a new column for each task, whose weights are initialized randomly.
Suppose we now want to learn a third task. Just add a third column, and connect the outputs of layer l in all previous columns to the inputs of layerl+1 in the new column:
This input connection is made through an adapter which helps to improve initial conditioning and also deals with the dimensionality explosion that would happen as more and more columns are added:
…we replace the linear lateral connection with a single hidden layer MLP (multi-layer perceptron). Before feeding the lateral activations into the MLP, we multiply them by a learned scalar, initialized by a random small value. Its role is to adjust for the different scales of the different inputs. The hidden layer on the non-linear adapter is a projection onto an n<sub>l</sub> dimensional subspace (n<sub>l</sub> is the number of units at layer _l).
As more tasks are added, this ensures that the number of parameters coming from the lateral connections remains in the same order.
Progressive networks in practice
The evaluation uses the A3C framework that we looked at yesterday. It’s superior convergence speed and ability to train on CPUs made it a natural fit for the large number of sequential experiments required for the evaluation. To see how well progressive networks performed, the authors compared both two and three-column progressive networks against four different baselines:
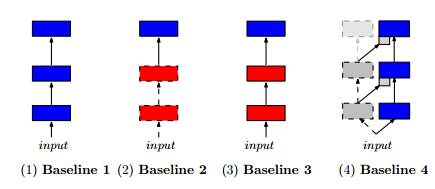
- (i) A single column trained on the target task (traditional network learning from scratch)
- (ii) A single column, using a model pre-trained on a source task, and then allowing just the final layer to be fine tuned to fit the target task
- (iii) A single column, using a model pre-trained on a source task, and then allowing the whole model to be fine tuned to fit the target task
- (iv) A two-column progressive network, but where the first column is simply initialized with random weights and then frozen.
The experiments include:
- Learning to play the Atari pong game as the initial task, and then trying to learn to play a variety of synthetic variants (extra noise added to the inputs, change the background colour, scale and translate the input, flip horizontally or vertically).
- Learning three source games (three columns, one each for Pong, RiverRaid, and Seaquest) and then seeing how easy it is to learn a new game – for a variety of randomly selected target games.
- Playing the Labyrinth 3D maze game – each column is a level (track) in the game, and we see how the network learns new mazes using information from prior mazes.
For the Pong challenge, baseline 3 (fine tuning a network pre-trained on Pong prior to the synthetic change) performed the best of the baselines, with high positive transfer. The progressive network outperformed even this baseline though, with better mean and median scores.
As the mean is more sensitive to outliers, this suggests that progressive networks are better able to exploit transfer when transfer is possible (i.e. when source and target domains are compatible).
For the game transfer challenge the target games experimented with include Alien, Asterix, Boxing, Centipede, Gopher, Hero, James Bond, Krull, Robotank, Road Runner, Star Gunner, and Wizard of Wor.
Across all games, we observe that progressive nets result in positive transfer in 8 out of 12 target tasks, with only two cases of negative transfer. This compares favourably to baseline 3, which yields positive transfer in only 5 out of 12 games.
The more columns (the more prior games the progressive network has seen), the more progressive networks outperform baseline 3.
Seaquest -> Gopher (two quite different games) is an example of negative transfer:
Sequest -> RiverRaid -> Pong -> Boxing is an example where the progressive networks yield significant transfer increase.
With the Labyrinth tests, the progressive networks once again yield more positive transfer than any of the baselines.
Limitations and future directions
Progressive networks are a stepping stone towards a full continual learning agent: they contain the necessary ingredients to learn multiple tasks, in sequence, while enabling transfer and being immune to catastrophic forgetting. A downside of the approach is the growth in number of parameters with the number of tasks. The analysis of Appendix 2 reveals that only a fraction of the new capacity is actually utilized, and that this trend increases with more columns. This suggests that growth can be addressed, e.g. by adding fewer layers or less capacity, by pruning [9], or by online compression [17] during learning. Furthermore, while progressive networks retain the ability to solve all K tasks at test time, choosing which column to use for inference requires knowledge of the task label. These issues are left as future work.
The other observation I would make is that the freezing prior columns certainly prevents catastrophic forgetting, but also prevents any ‘skills’ a network learns on subsequent tasks being used to improve performance on previous tasks. It would be interesting to see backwards transfer as well, and what could be done there without catastrophic forgetting.
