用导函数的图像判断原函数的单调性
前言
用导函数的图像判断原函数的单调性,其本质就是利用\(f'(x)\)的正负,判断\(f(x)\)的增减; 回顾:符号法则
典例剖析
- 给定\(f'(x)\)的图像,确定\(f(x)\)的单调性,最简单层次

分析:本题目考查对导函数的图像的解读能力,和应用图像的意识;
由于在\((4,5)\)上,有\(f^{\prime}(x)>0\)恒成立,故\(f(x)\)是增函数,故选\(C\).
- 用图像确定\(f'(x)\)的正负,确定\(f(x)\)的单调性,
分析:由图可知,
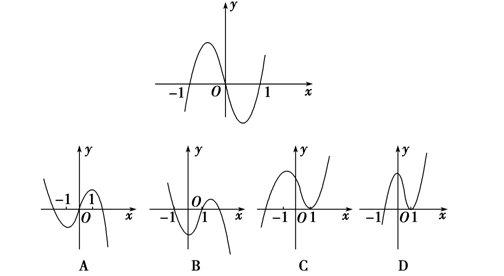
当\(x<-1\)时,\(y<0\),故由符号法则可知\(f'(x)>0\);
当\(-1<x<0\)时,\(y>0\),故由符号法则可知\(f'(x)<0\);
当\(0<x<1\)时,\(y<0\),故由符号法则可知\(f'(x)<0\);
当\(x>1\)时,\(y>0\),故由符号法则可知\(f'(x)>0\);
从而可知当\(x<-1\)时,\(f'(x)>0\),\(f(x)\nearrow\);
当\(-1<x<1\)时,\(f'(x)<0\),\(f(x)\searrow\);
当\(x>1\)时,\(f'(x)>0\),\(f(x)\nearrow\);故选C。
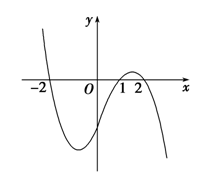
分析:当\(x<-2\)时,则有\(1-x>0\),又\(y>0\),故由符号法则可知\(f'(x)>0\);
当\(-2<x<1\)时,则有\(1-x>0\),又\(y<0\),故由符号法则可知\(f'(x)<0\);
当\(1<x<2\)时,则有\(1-x<0\),又\(y>0\),故由符号法则可知\(f'(x)<0\);
当\(x>2\)时,则有\(1-x<0\),又\(y<0\),故由符号法则可知\(f'(x)>0\);
从而可知当\(x<-2\)时,\(f'(x)>0\),\(f(x)\nearrow\);
当\(-2<x<2\)时,\(f'(x)<0\),\(f(x)\searrow\);
当\(x>2\)时,\(f'(x)>0\),\(f(x)\nearrow\);故选\(D\)。
*解不等式确定\(f^{\prime}(x)\)的正负,确定\(f(x)\)的单调性,
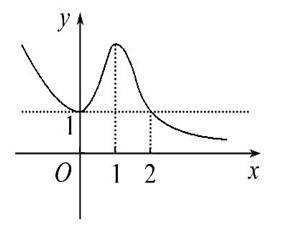
分析:结合图像可知,
当\(x\in(-\infty,2]\)时,\(2^{f^{\prime}(x)}≥1\), 即\(f^{\prime}(x)≥0\);当\(x\in (2,+\infty)\)时, \(2^{f^{\prime}(x)}<1\), 即\(f^{\prime}(x)<0\);
故函数\(y=f(x)\)的递减区间为\((2,+\infty)\)。故选\(D\)。
1、给定函数\(y=(x^2-3x+2)\cdot f'(x)\)的图像,先推断\(f'(x)\)的正负,再确定\(f(x)\)的单调性;
2、已知\((x^2-3x+2)\cdot f'(x)>0\),判断\(f(x)\)的单调性;

分析:由 \(y=f^{\prime}(x)\) 的图像是先上升后下降可知,函数 \(y=f(x)\)图像的切线的斜率先增大后减小,故选\(B\).

分析:由函数 \(f(x)\) 的图象可知, \(f(x)\) 在\((-\infty, 0)\)上单调递增, \(f(x)\) 在\((0,+\infty)\)上单调递减,
所以在区间\((-\infty, 0)\)上\(f'(x)>0\), 在\((0,+\infty)\)上\(f'(x)<0\),只有选项\(D\)满足;故选\(D\).
解析: 因为 \(f(x)=x-2\sin x,\) 所以\(f^{\prime}(x)=1-2\cos x\)
所以当\(0<x<\frac{\pi}{3}\)时, \(f'(x)<0\), \(f(x)\)单调递减;当\(\cfrac{\pi}{3}<x<\pi\)时, \(f^{\prime}(x)>0\),\(f(x)\)单调道增;
所以当 \(x=\cfrac{\pi}{3}\)时, \(f(x)\)有极小值,即最小值,
且 \(f(x)_{\min }=f(\cfrac{\pi}{3})=\cfrac{\pi}{3}-2\sin\cfrac{\pi}{3}=\cfrac{\pi}{3}-\sqrt{3}\)
又 \(f(0)=0\),\(f(\pi)=\pi\),所以 \(f(x)_{\max }=\pi\),
由题意得\(|f(x_{1})-f(x_{2})|\leqslant M\)等价于
\(M\geqslant|f(x)_{\max}-f(x)_{\min}|=\pi-(\cfrac{\pi}{3}-\sqrt{3})=\cfrac{2\pi}{3}+\sqrt{3}\),
所以\(M\) 的最小值为 \(\cfrac{2\pi}{3}+\sqrt{3}\), 故填写\(\cfrac{2\pi}{3}+\sqrt{3}\)。
(1) . 讨论\(f(x)\)的单调性;
分析:利用导数求导解决,
\(f'(x)=e^x(e^x-a)+e^x\cdot e^x-a^2=\)\(2e^{2x}-e^xa-a^2=(e^x-a)\cdot (2e^x+a)\),以下针对\(a\)分类讨论如下:
当\(a=0\)时,\(f'(x)>0\)恒成立,\(f(x)\)在区间\((-\infty,+\infty)\)上单调递增。
当\(a >0\)时,令\(f'(x)=0\),解得\(x=lna\),
则\(x\in(-\infty,lna)\)时,\(f'(x)<0\),即在区间\((-\infty,lna)\)上函数\(f(x)\)单调递减;
\(x\in(lna,+\infty)\)时,\(f'(x)>0\),即在区间\((lna,+\infty)\)上函数\(f(x)\)单调递增;
当\(a <0\)时,令\(f'(x)=0\),解得\(x=ln(-\cfrac{a}{2})\),
则\(x\in(-\infty,ln(-\cfrac{a}{2})\)时,\(f'(x)<0\),即在区间\((-\infty,ln(-\cfrac{a}{2}))\)上函数\(f(x)\)单调递减;
\(x\in(ln(-\cfrac{a}{2}),+\infty)\)时,\(f'(x)>0\),即在区间\((ln(-\cfrac{a}{2}),+\infty)\)上函数\(f(x)\)单调递增;
综上所述,
当\(a<0\)时,函数\(f(x)\)的单减区间是\((-\infty,ln(-\cfrac{a}{2}))\),单增区间是\((ln(-\cfrac{a}{2}),+\infty)\);
当\(a=0\)时,单增区间是\((-\infty,+\infty)\),无单减区间;
当\(a>0\)时,函数\(f(x)\)的单减区间是\((-\infty,lna)\),单增区间是\((lna,+\infty)\);
(2). 【2017全国卷1文科第21题高考真题】当\(x\ge 0\)时,\(f(x)\leq ax+1\),求\(a\)的取值范围。课件

分析:我们可以利用函数的性质做出函数的大致图像来寻找思路,\(f(0)=1\),\(f(\sqrt{2}-1)>1\),且函数在\((0,\sqrt{2}-1)\)上单调递增,在\((\sqrt{2}-1,+\infty)\)上单调递减,故可以做出函数的大致图像如右图所示。再者,函数\(f'(1)=1\),待编辑。
(2). 【2017全国卷2文科第21题高考真题】若 \(f(x)\ge 0\),求 \(a\) 的取值范围。
分析:由于要 \(f(x)\ge 0\) 恒成立,故只要求得 \(f(x)_{min}\ge 0\) 即可,又最小值要用到函数的单调性,而函数的单调性又是与 \(a\) 的取值有关,故应该关于 \(a\) 分类讨论:
当 \(a<0\) 时,函数 \(f(x)\) 的单减区间是 \((-\infty,ln(-\cfrac{a}{2}))\),单增区间是 \((ln(-\cfrac{a}{2}),+\infty)\);
故 \(f(x)_{min}\)\(=\)\(f(ln(-\cfrac{a}{2}))\)
\(=\)\(e^{ln(-\cfrac{a}{2})}(e^{ln(-\cfrac{a}{2})}-a)-a^2ln(-\cfrac{a}{2})\)\(=\)\(\cfrac{3a^2}{4}-a^2ln(-\cfrac{a}{2})\),
令 \(\cfrac{3a^2}{4}-a^2ln(-\cfrac{a}{2})\ge 0\) 得到\(a\ge-2e^{\frac{3}{4}}\),
故 \(-2e^{\frac{3}{4}}\leq a <0\);
当 \(a=0\) 时,\(f(x)=e^{2x}\ge 0\) 恒成立,故 \(a=0\) 满足题意;
当 \(a>0\) 时,函数 \(f(x)\) 的单减区间是 \((-\infty,lna)\),单增区间是 \((lna,+\infty)\);
故 \(f(x)_{min}=f(lna)=e^{lna}(e^{lna}-a)-a^2lna=-a^2lna\),
令\(-a^2lna\ge 0\),得到 \(a\leq 1\),故 \(0<a \leq 1\);
综上所述,取并集得到\(a\)的取值范围是\([-2e^{\frac{3}{4}},1]\)。
分析:\(f'(x)=\sin x+x\cdot\cos x-\sin x=x\cdot\cos x\);
在同一坐标系中,做出函数\(y=x\)和\(y=\cos x\)的图像,\(x\in (-\pi,\pi)\),
由符号法则可知,单调递增区间为\((-\pi,-\cfrac{\pi}{2})\)和\((0,\cfrac{\pi}{2})\);
单调递减区间为\((-\cfrac{\pi}{2},0)\)和\((\cfrac{\pi}{2},\pi)\);

 用导函数的图像判断原函数的单调性
用导函数的图像判断原函数的单调性

