数学概念的演变

前言

函数概念

函数的概念有两个，其一为初中的定义，称为传统定义，其二为高中的定义，称为近代定义。

传统定义：设在某变化过程中有两个变量\(x\)、\(y\)，如果对于\(x\)在某一范围内的每一个确定的值，\(y\)都有唯一确定的值与它对应，那么就称\(y\)是\(x\)的函数，\(x\)叫做自变量。我们将自变量\(x\)取值的集合叫做函数的定义域，和自变量\(x\)对应的\(y\)的值叫做函数值，函数值的集合叫做函数的值域。

近代定义：设 \(A\) ，\(B\) 都是非空的数集，\(f：x→y\) 是从 \(A\) 到 \(B\) 的一个对应法则，那么从 \(A\) 到 \(B\) 的映射 \(f：A→B\) 就叫做函数，记作 \(y=f(x)\)，其中 \(x∈A\)， \(y∈B\)，原象的集合 \(A\) 叫做函数 \(f(x)\) 的定义域，象的集合 \(C\) 叫做函数 \(f(x)\) 的值域，显然有\(C\subseteq B\)由于集合 \(B\) 中的元素不要求每一个都有原像的，而集合 \(A\) 中的每一个元素必须都有像，而且必须唯一；\(\quad\)。

• 对函数概念的理解

函数的两个定义本质是一致的，只是叙述概念的出发点不同，传统定义是从运动变化的观点出发，而近代定义是从集合、映射的观点出发。这样，就不难得知函数实质是从非空数集A到非空数集B的一个特殊的映射。

• 为什么要做这样的安排？

就高中的教学实践来看，高中阶段的学生接受映射这个抽象的数学概念都难度很大，更不用说初中学生了，故初中一般安排用传统定义来刻画函数，从运动变化的观点定义函数，便于学生理解和接受；随着学生的认知程度的提高，阅历的增加，接触函数的增多，用传统定义刻画的函数定义越来越不好解释函数的概念，比如迪利克雷函数，\(f(x)=\left\{\begin{array}{l}{1，x\in Q}\\{0，x\not\in Q，}\end{array}\right.\) 她本质的体现是一种对应，而不是运动变化过程。故需要对函数的定义做出调整；

同时还需要注意到，使用函数的近代定义来刻画函数，她还需要能向下兼容传统定义。这一点是满足的。故高中阶段采用先定义对应，然后在对应的概念基础上再定义映射，最后以映射为基础定义函数。

角的概念

• 初中定义：[静态定义]由公共端点的两条射线组成的图形，成为角。由此定义很容易理解其刻画的角的最大范围为\(\theta\in [0^{\circ}，360^{\circ}]\)。

如下图所示，

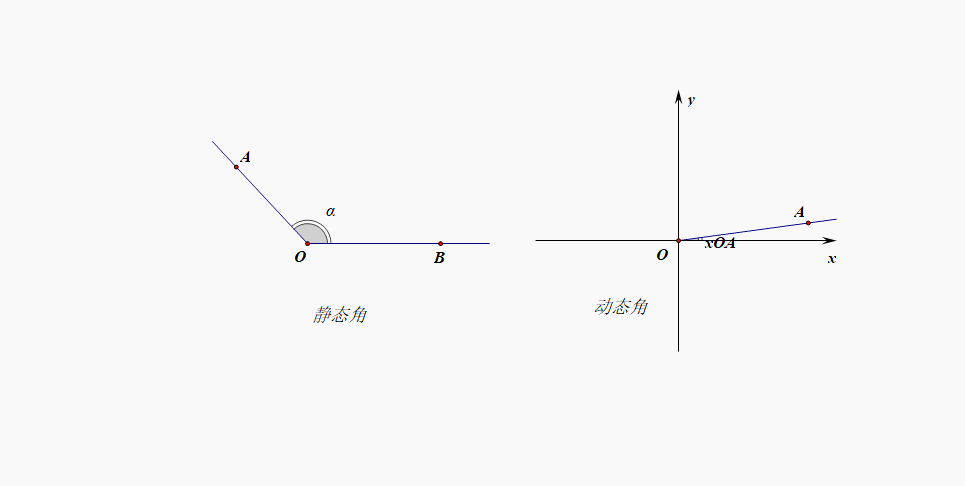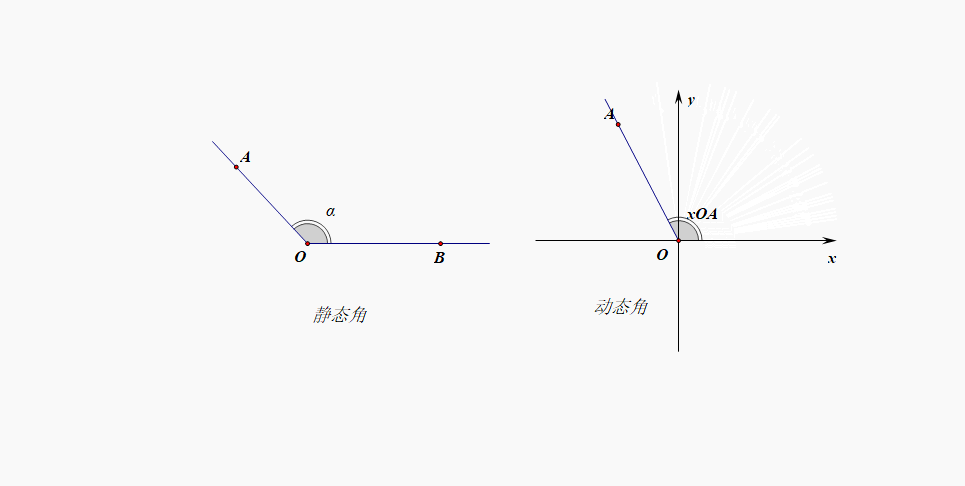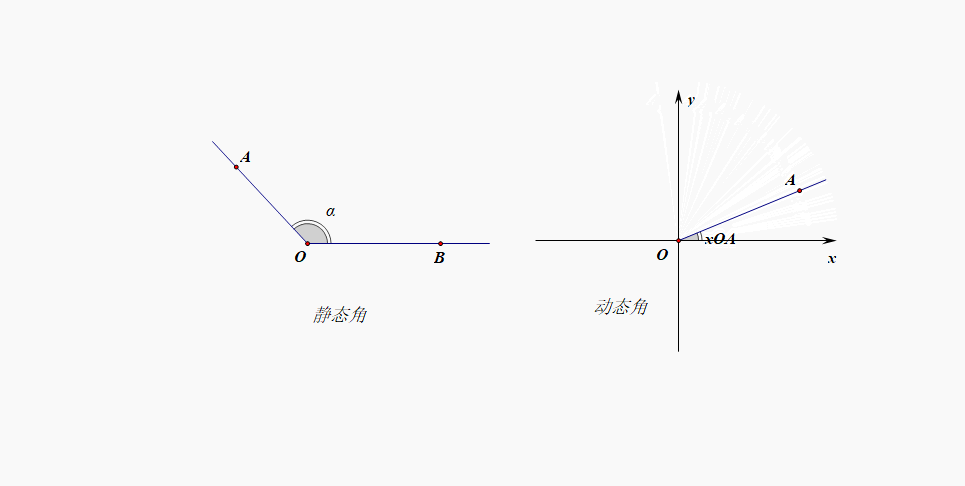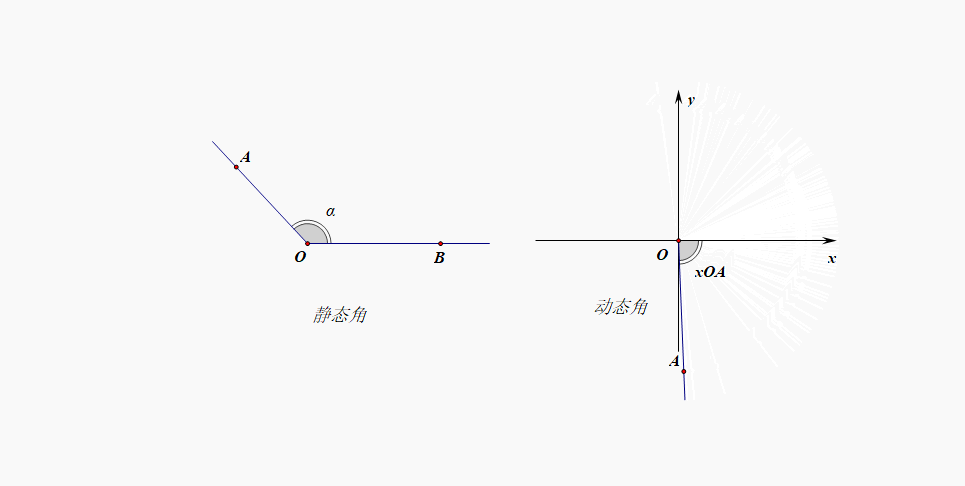
但是，在日常生活中，我们经常会拧开水瓶盖子，顺时针几圈或者逆时针几圈，显然这时候静态角的范围已经不够用了，需要调整，这时候就需要动态角的概念粉墨登场了。

• 高中定义：[动态定义]将一条射线的端点放置在直角坐标的原点位置，射线和\(x\)轴的非负半轴重合，此时如果逆时针旋转就形成了正角，范围可以拓展到\((0，+\infty)\)；如果顺时针旋转就形成了负角，范围可以拓展到\((-\infty，0)\)；如果不做选择就形成零角；这样采用动态定义，就能很容易将角的范围扩充到\((-\infty，+\infty)\)；

而且这种定义方式也是能兼容角的静态定义的。

三角函数概念

• 初中定义：同样由于受学生的认知能力和角的范围的限制，只是在 \(Rt\triangle\) 中定义， \(sin\theta=\cfrac{对边}{斜边}\) ， \(cos\theta=\cfrac{邻边}{斜边}\) ；这种定义的缺陷是三角函数的自变量 \(\theta\) 的范围只能是 \([0^{\circ}，90^{\circ}]\) .

而高中的角的范围已经扩充到了 \((-\infty，+\infty)\) ，显然上述的初中定义已经不能用了，需要更新，应该怎么更新呢？

• 高中定义：将角放置到平面直角坐标系中，初始边放置到\(x\)轴的非负半轴上，终边随其落在某个象限或者坐标轴上，然后在终边上任取一点(不是原点) \(P(x，y)\) ，则 \(r=|OP|=\sqrt{x^2+y^2}\) ，则 \(sin\theta=\cfrac{y}{r}\) ， \(cos\theta=\cfrac{x}{r}\) ， \(tan\theta=\cfrac{y}{x}\) ，

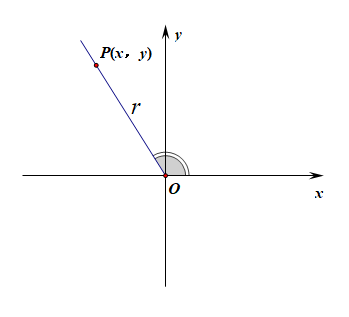
很显然，这种定义方式可以刻画 \((-\infty，+\infty)\) 范围内的任意一个角的三角函数，而且兼容范围 \([0^{\circ}，90^{\circ}]\) ，也就是说高中的三角函数的定义同样能解释初中的三角函数的定义，体现了数学概念发展的扬弃。

补充，只能用定义解题的题目。

切线概念

• 初中定义：由于受学生的认知能力的限制，直线和曲线[初中接触的曲线主要是圆]只有一个交点的情形，我们称为直线和曲线相切，比如直线和圆只有一个交点时，称为直线和圆相切，当然直线和圆相切时也必然只有一个交点；

• 高中定义：我们称曲线的割线的极限为切线，这一定义方式也是向下兼容的，即可以完美解释初中的定义，而且更有利于我们研究更多的曲线。

上图演示的是，圆的割线的的极限位置就是切线；

在高中切线的定义的支撑下，我们就不能再认为，直线和曲线只有一个交点时二者相切，也不能认为直线和曲线相切时只有一个交点。

• 当直线和曲线相切时，不一定只有一个交点，也可能有无数个交点，

比如直线\(y=1\)和曲线\(y=sinx\)，二者相切，有无数个交点。

• 当直线和曲线只有一个交点时，不一定是相切的，也可能相交，

比如直线\(x=1\)和抛物线\(y=(x-1)^2\)只有一个交点，但此时二者是相交的，不是相切的。