从三点共线到四点共面

复习回顾

【共线向量基本定理】如果向量 \(\vec{a}\neq \vec{0}\)，那么向量 \(\vec{b}\) 与向量 \(\vec{a}\) 共线的充要条件是：存在唯一实数 \(\lambda\)，使得向量 \(\vec{b}=\lambda\cdot \vec{a}\) .

三点共线

① 初中使用的三点共线的证明思路，距离的表示形式：若 \(|AB|+|BC|=|AC|\)，则 \(A\)，\(B\)，\(C\)三点共线。

② 高中使用的三点共线的证明思路，斜率表示形式: 若 \(k_{AB}=k_{AC}\)，则 \(A\)，\(B\)，\(C\)三点共线。

③ 高中使用向量表示形式使用的三点共线的证明思路：若 \(\overrightarrow{OC}=\lambda\overrightarrow{OA}+(1-\lambda)\overrightarrow{OB}\)，则 \(A\)，\(B\)，\(C\)三点共线。

或若 \(\overrightarrow{AB}=k\cdot \overrightarrow{AC}\)，则 \(A\)，\(B\)，\(C\)三点共线。

四点共面

【共面向量基本定理】如果向量 \(\vec{a}\)、\(\vec{b}\) 不共线，那么向量 \(\vec{c}\) 与向量 \(\vec{a}\)、向量 \(\vec{b}\) 共线的充要条件是：存在唯一实数对\(x\) 和 \(y\)，使得向量 \(\vec{c}=x\cdot \vec{a}+y\cdot \vec{b}\) .

【共面向量基本定理推论1】如果 \(A\)、\(B\)、\(C\)三点不共线，那么点 \(P\) 在平面 \(ABC\) 上的充要条件是：对空间上任意一点 \(O\) ，存在唯一实数对 \(x\)、\(y\)、\(z\)，且满足 \(x+y+z=1\)，使得 \(\overrightarrow{OP}\)\(=\)\(x\cdot\overrightarrow{OA}\)\(+\)\(y\cdot\overrightarrow{OB}\)\(+\)\(z\cdot\overrightarrow{OC}\) 。 证明^[1]

【共面向量基本定理推论2】如果 \(A\)、\(B\)、\(C\)三点不共线、那么点 \(P\) 在平面 \(ABC\) 上的充要条件是：对空间上任意一点 \(O\) ，存在唯一实数对 \(x\)、\(y\)、\(z\)，\(m\)，且满足 \(x+y+z+m=1\)，使得 \(x\cdot\overrightarrow{OP}\)\(+\)\(y\cdot\overrightarrow{OA}\)\(+\)\(z\cdot\overrightarrow{OB}\)\(+\)\(m\cdot\overrightarrow{OC}=\vec{0}\)。^[2]

【共面向量基本定理推论3】如果 \(A\)、\(B\)、\(C\)三点不共线、那么点 \(P\) 在平面 \(ABC\) 上的充要条件是：对空间上任意一点 \(O\) ，存在唯一实数对 \(x\)、\(y\)，使得 \(\overrightarrow{OP}\)\(=\)\((1-x-y)\cdot\overrightarrow{OA}\)\(+\)\(x\cdot\overrightarrow{OB}\)\(+\)\(y\cdot\overrightarrow{OC}\)。

四点共面证明思路

① 思路一：若任意四点的连线平行或者相交，则此四点必然共面。

比如，线段 \(AC\) 和线段 \(BD\) 平行[不妨称平行线法]或者相交[不妨称相交线法]，则可知点\(A\)，\(B\)，\(C\)，\(D\)四点共面。

② 思路二：四点共面的问题，可以转化为向量共面的问题，

比如，要证明 \(P\)、\(A\)、\(B\)、\(C\) 四点共面，只要能证明\(\overrightarrow{PA}\)\(=\)\(m\cdot\overrightarrow{PB}\)\(+\)\(n\cdot\overrightarrow{PC}\)，

或者\(\overrightarrow{OP}\)\(=\)\(x\cdot\overrightarrow{OA}\)\(+\)\(y\cdot\overrightarrow{OB}\)\(+\)\(z\cdot\overrightarrow{OC}\)，其中\(x+y+z=1\)。

典例剖析

如图， 已知平行四边形 \(ABCD\)， 过平面 \(AC\) 外一点 \(O\) 作射线 \(OA\)，\(OB\)， \(OC\)， \(OD\)， 在四条射线上分别取点 \(E\)，\(F\)，\(G\)，\(H\)，使 \(\cfrac{OE}{OA}=\cfrac{OF}{OB}=\cfrac{OG}{OC}=\cfrac{OH}{OD}=k\)。 求证: \(E\)， \(F\)， \(G\)， \(H\) 四点共面。

法一分析：平行线法，可以通过证明 \(AB//EF\)， \(CD//GH\)，从而证明 \(EF//GH\)，从而证明\(E\)， \(F\)， \(G\)， \(H\) 四点共面。

【证明一】：由已知条件\(\cfrac{OE}{OA}=\cfrac{OF}{OB}=k\)，可得，\(AB//EF\) ^[3]

同理，由条件 \(\cfrac{OG}{OC}=\cfrac{OH}{OD}=k\)，可得，\(CD//GH\)，

则有 \(EF//GH\)，则可得 \(E\)，\(F\)，\(G\)，\(H\) 四点共面。^[4]

法二分析：向量法，欲证 \(E\)， \(F\)，\(G\)， \(H\) 四点共面， 只需证明 \(\overrightarrow{EH}\)， \(\overrightarrow{EF}\)，\(\overrightarrow{EG}\) 共面。 而由已知 \(\overrightarrow{AD}\)， \(\overrightarrow{AB}\)， \(\overrightarrow{AC}\) 共面，可以利用向量运算由 \(\overrightarrow{AD}\)， \(\overrightarrow{AB}\)， \(\overrightarrow{AC}\) 共面的表达式推得 \(\overrightarrow{EH}\)，\(\overrightarrow{EF}\)， \(\overrightarrow{EG}\) 共面的表达式。

【证明二】：由于四边形 \(ABCD\) 是平行四边形，则向量 \(\overrightarrow{AC}\)，\(\overrightarrow{AD}\)，\(\overrightarrow{AB}\) 共面，

即存在唯一的实数对 \(m\)、\(n\)，使得 \(\overrightarrow{AC}=\)\(m\cdot\overrightarrow{AD}+\)\(n\cdot\overrightarrow{AB}\)，

又由于 \(\overrightarrow{AC}\)\(=\)\(\overrightarrow{OC}\)\(-\)\(\overrightarrow{OA}\)，\(\overrightarrow{AD}\)\(=\)\(\overrightarrow{OD}\)\(-\)\(\overrightarrow{OA}\)，\(\overrightarrow{AB}\)\(=\)\(\overrightarrow{OB}\)\(-\)\(\overrightarrow{OA}\)，

代入即得，\(\overrightarrow{OC}-\overrightarrow{OA}=\)\(m\cdot(\overrightarrow{OD}-\overrightarrow{OA})+\)\(n\cdot(\overrightarrow{OB}-\overrightarrow{OA})\)，(*)

又由 \(\cfrac{OE}{OA}=\cfrac{OF}{OB}=\cfrac{OG}{OC}=\cfrac{OH}{OD}=k\) 可得，

\(\overrightarrow{OE}=k\cdot\overrightarrow{OA}\)，\(\overrightarrow{OG}=k\cdot\overrightarrow{OC}\)，\(\overrightarrow{OH}=k\cdot\overrightarrow{OD}\)，\(\overrightarrow{OF}=k\cdot\overrightarrow{OB}\)，

给上述已知 (*) 两边同乘以 \(k\)，代换整理得到，

\(k\cdot\overrightarrow{OC}-k\cdot\overrightarrow{OA}=\)\(m\cdot(k\cdot\overrightarrow{OD}-k\cdot\overrightarrow{OA})+\)\(n\cdot(k\cdot\overrightarrow{OB}-k\cdot\overrightarrow{OA})\)，

即 \(\overrightarrow{OG}-\overrightarrow{OE}=\)\(m\cdot(\overrightarrow{OH}-\overrightarrow{OE})+\)\(n(\cdot\overrightarrow{OF}-\overrightarrow{OE})\)，

即 \(\overrightarrow{EG}=m\cdot\overrightarrow{EH}+n\cdot\overrightarrow{EF}\)，

则可知，向量 \(\overrightarrow{EG}\)、\(\overrightarrow{EH}\)、\(\overrightarrow{EF}\)共面，即可得 \(E\)，\(F\)，\(G\)，\(H\) 四点共面。

如图所示，在空间四边形\(ABCD\)中，点\(E\)，\(H\)分别是边\(AB\)，\(AD\)的中点，点\(F\)，\(G\)分别是边\(BC\)，\(CD\)上的点，且\(\cfrac{CF}{CB}=\cfrac{CG}{CD}=\cfrac{2}{3}\)，则下列说法正确的是【\(\qquad\)】

①\(EF\)与\(GH\)平行；

②\(EF\)与\(GH\)异面；

③\(EF\)与\(GH\)的交点\(M\)可能在直线\(AC\)上，也可能不在直线\(AC\)上；

④\(EF\)与\(GH\)的交点\(M\)一定在直线\(AC\)上；

$A.①④$ $B.④$ $C.①③$ $D.②$

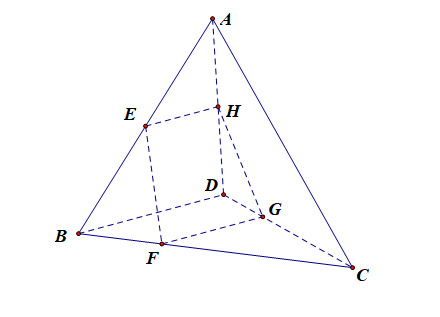
分析：连接\(EH\)，\(FG\)，由题意可知，\(EH//BD\)，\(FG//BD\)，故\(EH//FG\)，且有\(EF\)和\(GH\)不平行，故四边形\(EFGH\)为梯形，所以\(E,F,G,H\)四点共面。故①②错误；

延长\(FE\)和\(GH\)必然交于予一点，两线的交点一定在平面在\(ACD\)上，延长\(FE\)和\(CA\)必然交于一点，两线的交点一定在平面\(ACB\)上，故两线的交点一定在平面\(ACD\)和平面\(ACB\)的交线\(AC\)上，故③错误；

综上所述，故选\(B\)；

另解：[动态观点]设想线段\(FG\)平行移动[和\(BD\)平行]，当\(FG\)缩减为点\(C\)时，说明④正确，当\(FG\)扩充为线段\(BD\)时，也说明④正确，故①②③错误，故选\(B\).

---

1. 共面向量基本定理推论1的证明；
   证明：必要性，由于 \(A\)、\(B\)、\(C\)三点不共线，则向量 \(\overrightarrow{AB}\)、\(\overrightarrow{AC}\)不共线，
   又点 \(P\) 在平面 \(ABC\) 内，则向量 \(\overrightarrow{AP}\)、\(\overrightarrow{AB}\)、\(\overrightarrow{AC}\)共面，
   由共面向量基本定理可知，存在唯一的实数对 \(m\)、\(n\)，使得 \(\overrightarrow{AP}\)\(=\)\(m\cdot\overrightarrow{AB}\)\(+\)\(n\cdot\overrightarrow{AC}\) .
   又由于 \(\overrightarrow{AP}\)\(=\)\(\overrightarrow{OP}\)\(-\)\(\overrightarrow{OA}\)，\(\overrightarrow{AB}\)\(=\)\(\overrightarrow{OB}\)\(-\)\(\overrightarrow{OA}\)，\(\overrightarrow{AC}\)\(=\)\(\overrightarrow{OC}\)\(-\)\(\overrightarrow{OA}\)，
   代入得到，\(\overrightarrow{OP}-\overrightarrow{OA}=m\cdot(\overrightarrow{OB}-\overrightarrow{OA})+n\cdot(\overrightarrow{OC}-\overrightarrow{OA})\) ，
   整理得到，\(\overrightarrow{OP}=(1-m-n)\cdot\overrightarrow{OA}+m\cdot\overrightarrow{OB}+n\cdot\overrightarrow{OC}\) ，
   做简单的代换，令 \(1-m-n=x\)，\(m=y\)，\(n=z\)，即得到
   \(\overrightarrow{OP}\)\(=\)\(x\cdot\overrightarrow{OA}\)\(+\)\(y\cdot\overrightarrow{OB}\)\(+\)\(z\cdot\overrightarrow{OC}\)，且满足 \(x+y+z=1\)；
   充分性，由于 \(A\)、\(B\)、\(C\)三点不共线，则向量 \(\overrightarrow{AB}\)、\(\overrightarrow{AC}\)不共线，
   对空间上任意一点 \(O\) ，存在唯一实数对 \(x\)、\(y\)、\(z\)，且满足 \(x+y+z=1\)，使得 \(\overrightarrow{OP}\)\(=\)\(x\cdot\overrightarrow{OA}\)\(+\)\(y\cdot\overrightarrow{OB}\)\(+\)\(z\cdot\overrightarrow{OC}\) ，
   仿上做代换令 \(x=1-m-n\)，\(y=m\)，\(z=n\)，即得到 \(\overrightarrow{OP}=(1-m-n)\cdot\overrightarrow{OA}+m\cdot\overrightarrow{OB}+n\cdot\overrightarrow{OC}\) ，
   又由于 \(\overrightarrow{AP}\)\(=\)\(\overrightarrow{OP}\)\(-\)\(\overrightarrow{OA}\)，\(\overrightarrow{AB}\)\(=\)\(\overrightarrow{OB}\)\(-\)\(\overrightarrow{OA}\)，\(\overrightarrow{AC}\)\(=\)\(\overrightarrow{OC}\)\(-\)\(\overrightarrow{OA}\)，
   整理得到，存在唯一的实数对 \(m\)、\(n\)，使得 \(\overrightarrow{AP}\)\(=\)\(m\cdot\overrightarrow{AB}\)\(+\)\(n\cdot\overrightarrow{AC}\)
   由共面向量基本定理可知，向量 \(\overrightarrow{AP}\)、\(\overrightarrow{AB}\)、\(\overrightarrow{AC}\)共面，
   即点 \(P\) 在平面 \(ABC\) 上。证毕。 ↩︎

2. 推论 2 和推论 3 本质上是推论 1 的不同形式的改写。 ↩︎

3. 平行线分线段成比例定理[又称为平行截割定理]的推论：平行于三角形一边的直线截其他两边(或者两边的延长线)，截得的三角形与原三角形的对应边成比例.
   平行截割定理推论的逆定理：如果一条直线截三角形的两边(或者两边的延长线)所得的对应线段成比例，那么这条直线平行于三角形的第三边。 ↩︎

4. 两条平行线确定一个平面。两条相交直线确定一个平面。
   问题：可以利用相交线法证明吗？比如通过证明直线 \(EG\) 和 \(FH\) 相交可得四点共面。 ↩︎