半正多面体

前言

正多边形内角和公式：\((n-2)\)\(\cdot\)\(180^{\circ}\) ^[1]，故正八边形的每一个内角为 \(\cfrac{3\pi}{4}\)；正多边形外角和为：\(360^{\circ}\)；^[2]

典例剖析

【2019年高考数学试卷理科新课标Ⅱ第16题】中国有悠久的金石文化，印信是金石文化的代表之一。印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”，半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体体现了数学的对称美，图2是一个棱数为\(48\)的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为\(1\)，则该半正多面体共有__________个面，其棱长为_____________。

分析：半正多面体的制作过程，如下图所示；

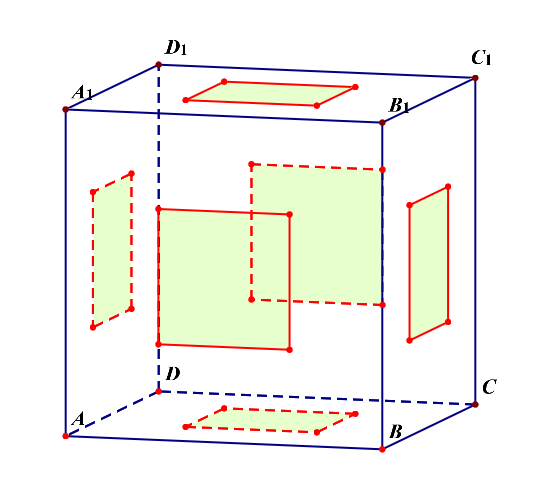
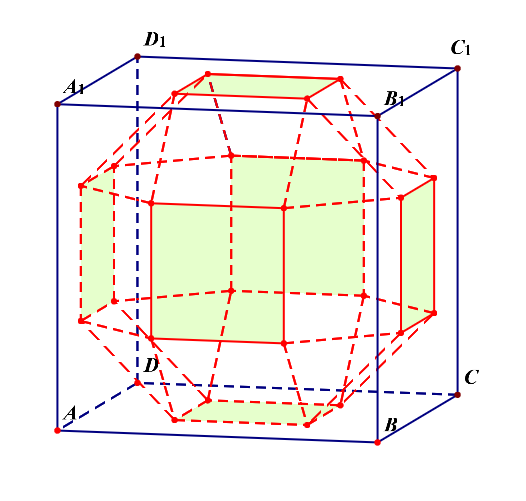
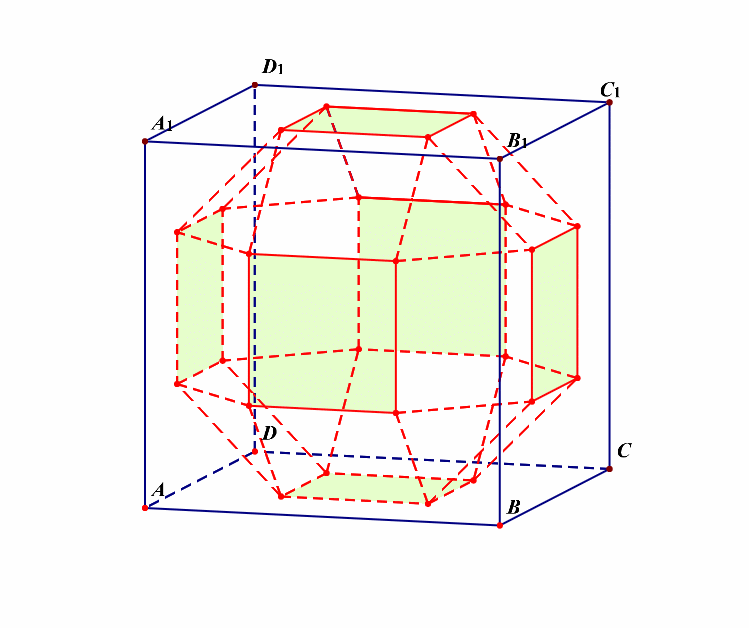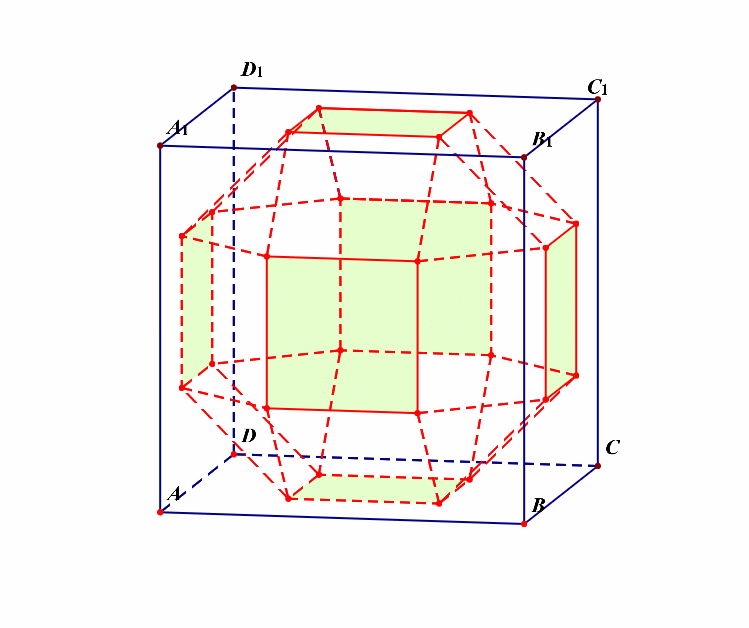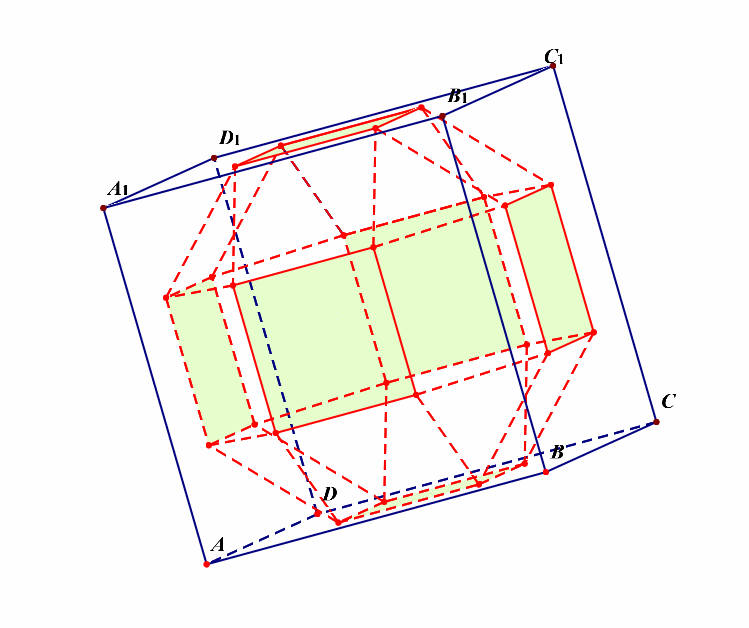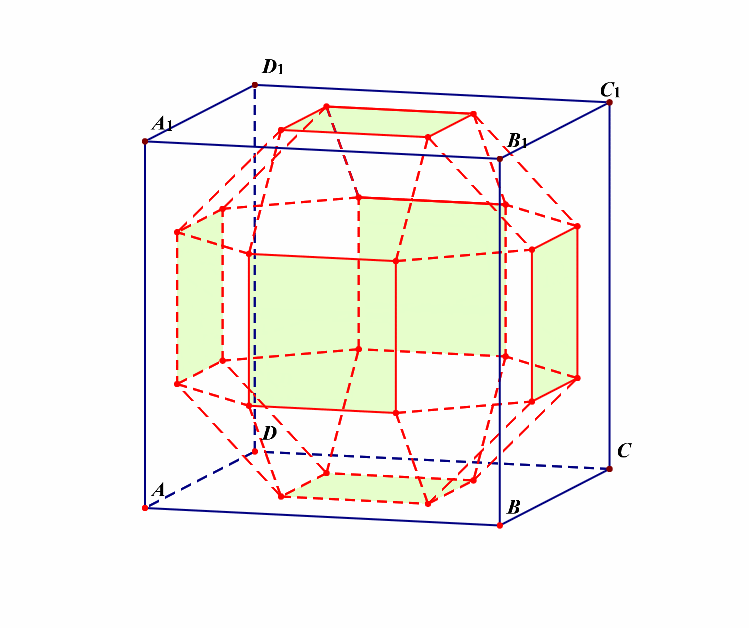
解析：如果我们将其看成是三层的，则每一层都有\(8\)个面，再外加上下两个面，故共有\(3\times 8+2=26\)个面。

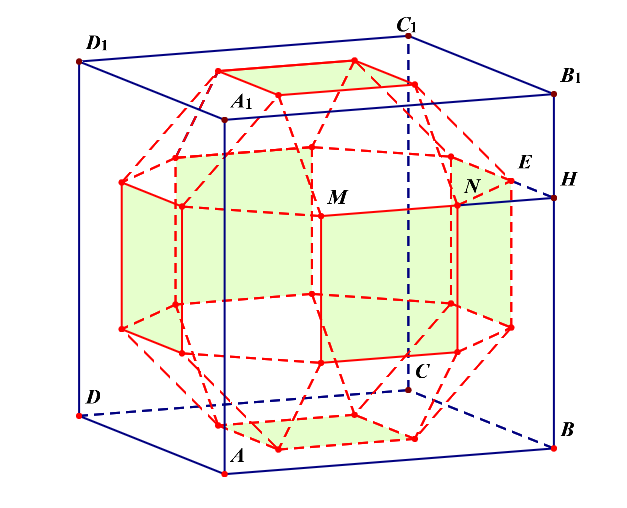
如图所示，设棱长为\(x\)，即\(MN=NE=x\)，由\(\triangle EHN\)为等腰直角三角形，

由\(NE=x\)，则可知\(NH=\cfrac{\sqrt{2}}{2}x\)，又\(MN+2NH=1\)，

则\(x+2\times \cfrac{\sqrt{2}}{2}x=1\)，即\((\sqrt{2}+1)x=1\)，解得\(x=\sqrt{2}-1\).

综上可知，此半正多面体共有\(26\)个面，棱长为\(\sqrt{2}-1\)。

【解后反思】

1、求其表面积；

2、求其体积；

3、求其内切球的半径；

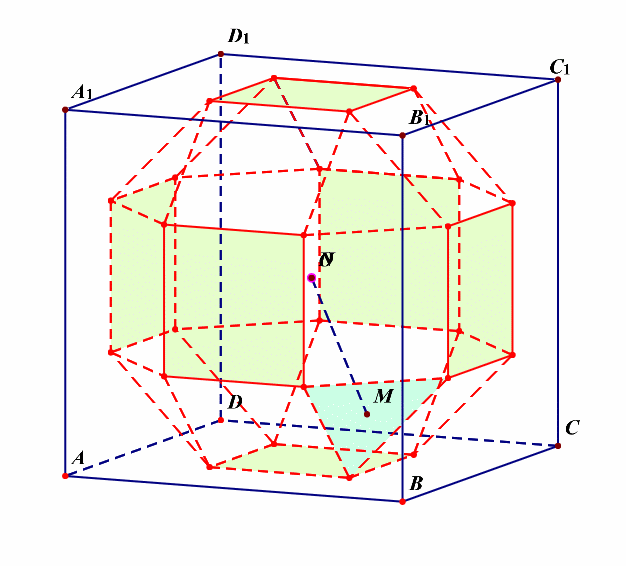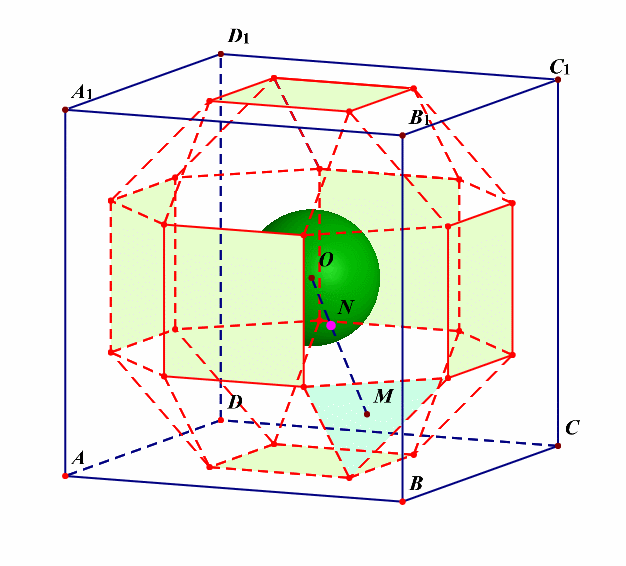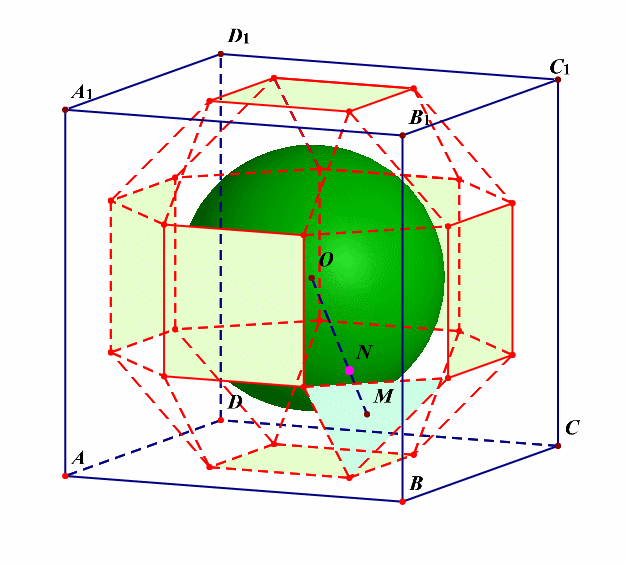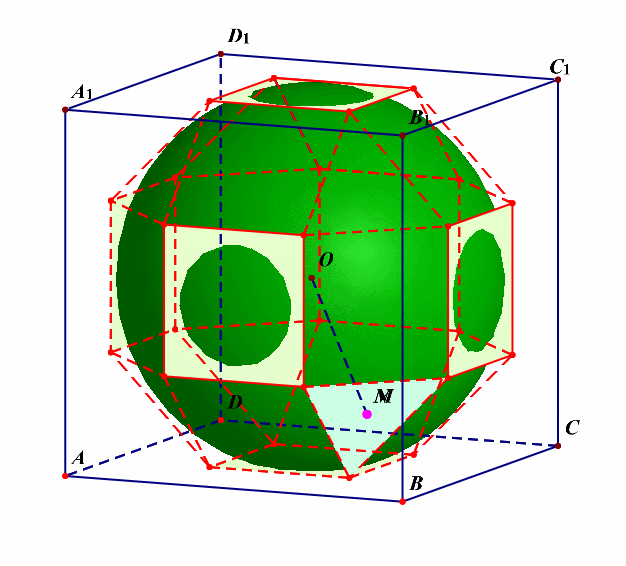
分析：由这个动画可以看出，该半正多面体没有内切球。

4、求其外接球的半径；

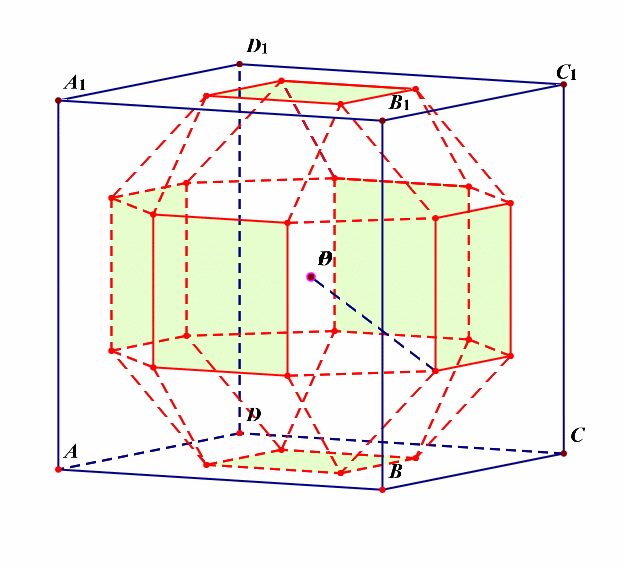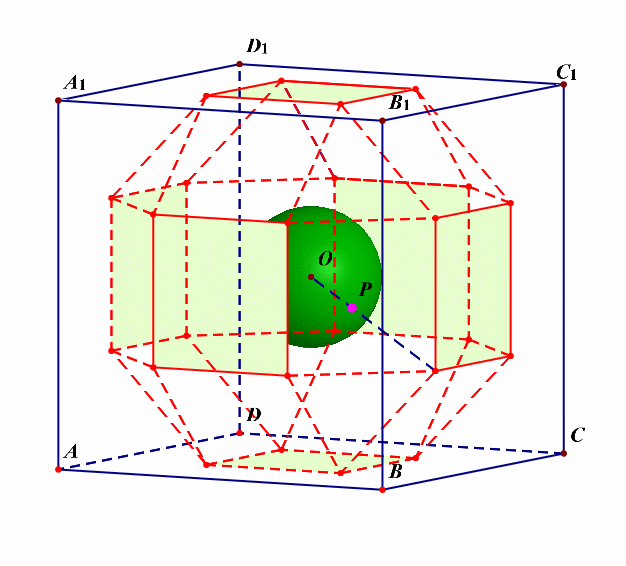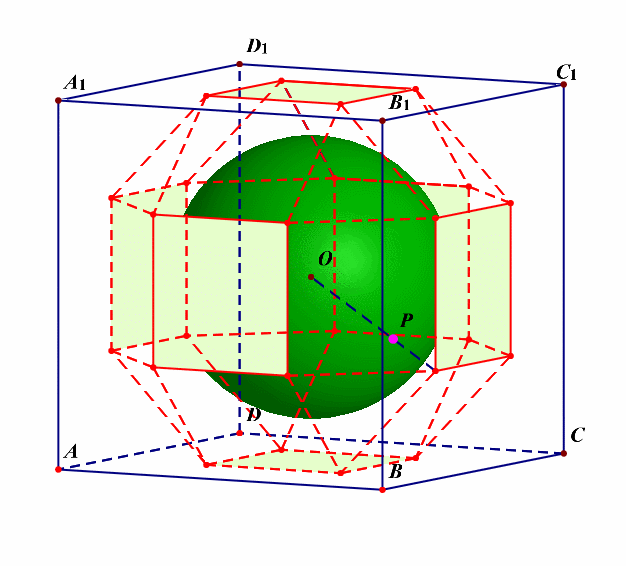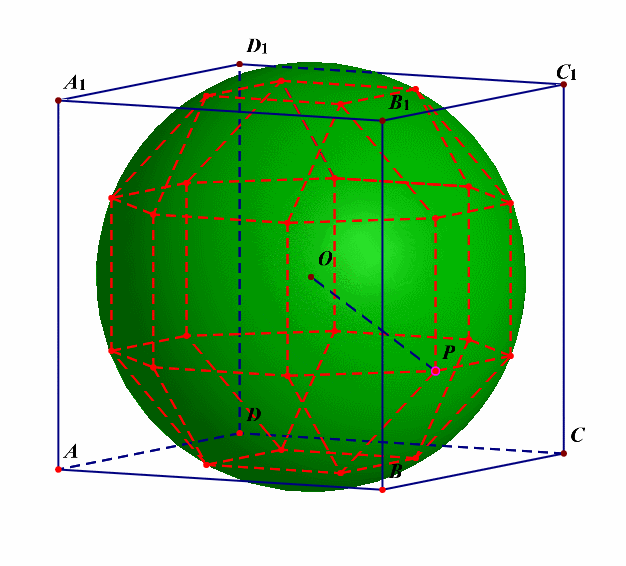
外接球的半径可以借助下图来求解。

5、古典概型中的几何体计数

【2024高一训练题目】如图，该多面体的表面由 \(18\) 个全等的正方形和 \(8\) 个全等的正三角形构成，该多面体的所有顶点都在同一个正方体的表面上 . 若 \(MN=\sqrt{2}\)， 则 【\(\qquad\)】

$A$.$AB=3\sqrt{2}$

$B.$该多面体外接球的表面积为$(10+4\sqrt{2})\pi$

$C.$直线 $MG$与直线 $PQ$的夹角为 $\cfrac{\pi}{4}$

$D.$二面角 $G-NH-P$ 的余弦值为 $-\cfrac{\sqrt{2}}{2}$

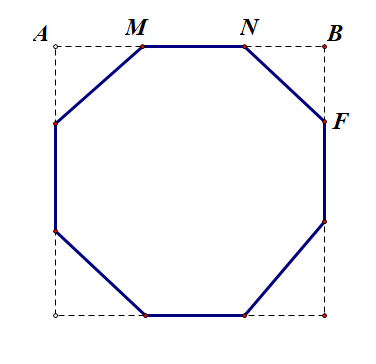
解：对选项 \(A\) 而言，沿着平面 \(MNF\) 做截面，则此截面截取正方体得到的是正方形，截取半正多面体得到的是正八边形，做俯视如图所示，且可知 \(MN=NF=\sqrt{2}\)，故 \(NB=1\)，则 \(AM=1\)，故 \(AB\)\(=\)\(AM\)\(+\)\(MN\)\(+\)\(NB\)\(=\)\(2\)\(+\)\(\sqrt{2}\)，选项 \(A\) 错误；

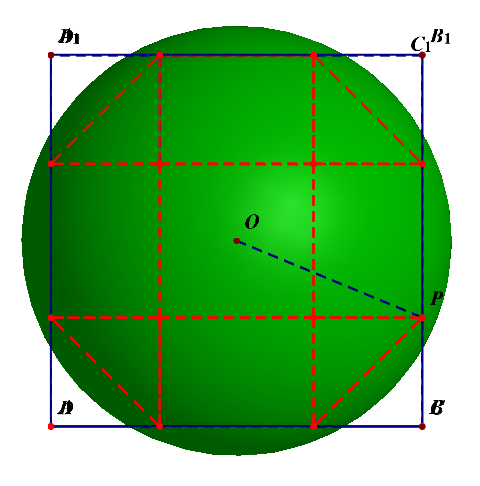
对选项 \(B\) 而言，可借助下图研究半正多面体的外接球的半径，外接球的球心是正方体的中心 \(O\)，点 \(O\) 在右侧面的正射影是右侧面正方形的中心，记为点 \(O'\)，取半正多面体的任意一个顶点[比如动点 \(P\) 的最后的位置]，则 \(\triangle OO'P\) 是 \(Rt\triangle\)，且 \(OO'\)\(=\)\(\cfrac{AB}{2}\)\(=\)\(\cfrac{2+\sqrt{2}}{2}\)，\(O'P=1\)[\(O'P\) 应该是边长为 \(\sqrt{2}\) 的正方形的对角线的一半]，则由勾股定理可得，半正多面体的半径 \(R=OP=\sqrt{OO'^2+O'P^2}=\sqrt{\cfrac{10+4\sqrt{2}}{4}}\)，

故半正多面体的外接球的表面积 \(S_{表}=4\pi R^2=4\pi\times\cfrac{10+4\sqrt{2}}{4}=(10+4\sqrt{2})\pi\)，故选项 \(B\) 正确；

对选项 \(C\) 而言，直线 \(MG//AD//BC\)，标记下底面上的和直线 \(BC\) 平行的直线为 \(B'C'\)，则直线 \(B'C'\) 与直线 \(PQ\)的夹角为 \(\cfrac{\pi}{4}\)，故直线 \(MG\)与直线 \(PQ\)的夹角为 \(\cfrac{\pi}{4}\)，即选项 \(C\) 正确；

对选项 \(D\) 而言，从图上应该能比较容易的看出来，二面角 \(G-NH-P\) 的平面角刚好是正八边形的内角为 \(135^{\circ}\)，故 \(G-NH-P\) 的余弦值为 \(-\cfrac{\sqrt{2}}{2}\)，即选项 \(D\) 正确；

综上所述，选 \(BCD\) .

---

1. 从正 \(n\) 边形的中心向各个顶点引线段，这样把正 \(n\) 边形就分为 \(n\) 个三角形，其所有内角之和是 \(n\) 个三角形的内角和减去中心位置的 \(n\) 个角之和，故正多边形内角和公式：\((n-2)\)\(\cdot\)\(180^{\circ}\)；其实条件可以弱化为只要是凸多边形，其内角和都是 \((n-2)\)\(\cdot\)\(180^{\circ}\)；配图说明 ↩︎

2. 正 \(n\) 边形的内角和定理:正 \(n\) 边形的内角和为 \((n-2)\times180^{\circ}\)；正 \(n\) 边形的外角和定理：正 \(n\) 边形的外角为其对应内角的邻补角，正 \(n\) 边形的外角和为 \(360^{\circ}\) . 证明：在正 \(n\) 边形的每一个顶点处，形成一个周角，此周角包含两个正 \(n\) 边形的内角 \(\alpha=\cfrac{(n-2)\times180^{\circ}}{n}\) 和两个外角 \(\theta\)，则 \(2\alpha+2\theta=360^{\circ}\)，代入解得外角为 \(\theta=\cfrac{360^{\circ}}{n}\)，故正 \(n\) 边形的外角和为 \(360^{\circ}\) . 参考图形 ↩︎