近似计算和估值计算

前言

2019年的考试说明中对运算能力的详细描述是这样的：会根据法则、公式进行变形和正确运算，能根据问题的条件寻找与设计合理、简捷的运算途径，能根据问题要求进行估算或近似计算。

运算求解能力是思维能力和运算技能的结合。运算包括对数值的计算和近似计算，对数学表达式的变形，对几何图形相关几何量的计算求解等。运算求解能力包括分析运算条件、探究运算方向、选择运算公式、确定运算程序等一系列过程中的思维能力，也包括在实施运算过程中遇到障碍而调整运算的能力。

对运算求解能力的考查，不仅包括数的运算，还包括式的运算，兼顾对算理和逻辑推理的考查。考查主要是以含字母的式的运算为主，包括数字的计算、代数式和某些超越式的恒等变形、集合的运算、解方程与不等式、三角恒等变形、求导运算、概率计算、向量运算和几何图形中的计算等。运算结果具有存在性、确定性和最简性。
运算求解能力是一项基本能力，在代数、三角函数、立体几何、平面解析几何、统计与概率、导数、向量等内容中都有所体现。运算的作用不仅是只求出结果，有时还可以辅助证明(以算代证)。运算能力是最基础的又是应用最广的一种能力，高考中对运算求解能力的考查主要体现在运算的合理性、准确性、熟练性、简捷性。

近似计算

• 根式：\(\sqrt{2}=1.414\cdots\)；\(\sqrt{3}=1.732\cdots\)；\(\sqrt{5}=2.236\cdots\)；\(\sqrt{10}=3.162\cdots\)；

• 分式：\(\cfrac{1}{3}=0.333\cdots\)；\(\cfrac{\pi}{2}=1.57079\cdots\)；

• 指数式：\(e=2.718281\cdots\)；\(e^2=7.389\cdots\)；

• 对数式：\(lg2\approx 0.3010\)；\(lg3\approx 0.4771\)；\(ln2\approx 0.6931\)；\(lg3\approx 1.097\)；

• 三角式：\(sin18^{\circ}=\cfrac{\sqrt{5}-1}{2}\)；

典例剖析

【2020年新课标Ⅰ理科数学第\(12\)题】【上例的延申题】 若 \(2^{a}+\log_{2}a=4^{b}+2\log_{4}b\)， 则 【\(\quad\)】

$A.a > 2b$ $B.a < 2b$ $C.a > b^2$ $D.a < b^2$

解析：因为 \(2^{a}+\log _{2} a=4^{b}+2 \log _{4} b=2^{2 b}+\log _{2}b\)，

又由于 \(2^{2b}+\log_{2}b<2^{2b}+\log_{2}2b=2^{2b}+\log_{2}b+1\)，

故 \(2^{a}+\log_{2}a<2^{2b}+\log_{2}2b\)，

此时令 \(f(x)=2^{x}+\log_{2}x\)， 则上述条件变化为 \(f(a)<f(2b)\)这样就能利用新构造的函数的性质比较大小，此时主要用到定义域和单调性。\(\quad\)，

由指对数函数的单调性可得 \(f(x)\) 在 \((0,+\infty)\) 内单调递增，且 \(f(a)<f(2b)\)，

则得到 \(a<2b\)，故选：\(B\) .

法2：赋值法+估值法，相比上述解法，思维的层次低了一些。

令 \(a=1\)，则 左边\(=2+0=2\)，此时由于 \(f(b)=4^b+2\log_4b\)单调递增，\(f(\cfrac{1}{2})=2-1<2\)，\(f(1)=4+0>2\)，故 \(\cfrac{1}{2}<b<1\)，这样就能排除 \(A\) 和 \(C\)，

令 \(b=1\)，则 右边\(=4+0=4\)，此时由于 \(g(a)=2^b+\log_2a\)单调递增，\(g(\cfrac{3}{2})\)\(=\)\(2^{\frac{3}{2}}\)\(+\)\(\log_2\frac{3}{2}\)\(=\)\(2\sqrt{2}\)\(+\)\(\log_23-1\)\(<\)\(4\)，\(g(2)=2^2+1>4\)，故 \(\cfrac{3}{2}<a<2\)，这样就能排除 \(D\)，

综上所述，故选 \(B\) .

求\(0.998^6\)的误差小于\(0.001\)的近似值是_____________。

分析：\(0.998^6=(1-0.002)^2=1+6\times (-0.002)+15\times (-0.002)^2+\cdots+(-0.002)^6\)

由于\(T_3=15\times (-0.002)^2=0.00006<0.001\)，

即第3项以后的项的绝对值都小于\(0.001\)，

所以从第3项起，以后的项可以忽略不计，

即\(0.998^6=(1-0.002)^2\approx 1+6\times (-0.002)=0.998\)。

故\(0.998^6\)的误差小于\(0.001\)的近似值是\(0.998\)。

【2019年高考数学全国卷理科新课标Ⅱ第4题改编】将高考真题中的物理知识背景省略，高度抽象就得到了如下的数学题目：

已知公式：\(\cfrac{M_1}{(R+r)^2}+\cfrac{M_2}{r^2}=(R+r)\cfrac{M_1}{R^3}\)，且已知\(\alpha=\cfrac{r}{R}\)，\(\cfrac{3\alpha^3+3\alpha^4+\alpha^5}{(1+\alpha)^2}\approx 3\alpha^3\)，试用\(M_1\)，\(M_2\)，\(R\)表示\(r\)的近似值；

$A.\sqrt{\cfrac{M_2}{M_1}}\cdot R$ $B.\sqrt{\cfrac{M_2}{2M_1}}\cdot R$ $C.\sqrt[3]{\cfrac{3M_2}{M_1}}\cdot R$ $D.\sqrt[3]{\cfrac{M_2}{3M_1}}\cdot R$

分析：联系到本年度的Ⅱ卷高考数学题目的解答，首先要突破的是对题意的理解，大体意思就是，给定了一个方程，要求你将方程中的\(r\)求解出来，但是由于是用手工计算，为了降低难度，给了一个近似参考公式，你必须使用这个近似计算公式，才能顺利求解。理解了题意之后，还有一个问题，就是该如何使用近似计算公式。由于近似计算中提到了\(\alpha=\cfrac{r}{R}\)，所以我们需要首先让方程中出现\(\alpha\)，使用\(\cfrac{r}{R}=\alpha\)代换，求解到最后，再使用\(\alpha=\cfrac{r}{R}\)，让式子中出现\(r\)，计算即可。

解析：给方程的两边，同时乘以\(R^2\)，得到\(\cfrac{R^2\cdot M_1}{(R+r)^2}+\cfrac{R^2\cdot M_2}{r^2}=(R+r)\cfrac{R^2\cdot M_1}{R^3}\)，

即\(\cfrac{M_1}{\frac{(R+r)^2}{R^2}}+\cfrac{M_2}{\frac{r^2}{R^2}}=(R+r)\cfrac{M_1}{\frac{R^3}{R^2}}\)，变形得到，

\(\cfrac{M_1}{(1+\alpha)^2}+\cfrac{M_2}{\alpha^2}=(R+r)\cfrac{M_1}{R}\)，即\(\cfrac{M_1}{(1+\alpha)^2}+\cfrac{M_2}{\alpha^2}=(1+\alpha)M_1\)，

然后通分整理，得到，\(\alpha^2M_1+(1+\alpha)^2M_2=(1+\alpha)^3\cdot \alpha^2M_1\)，

则有\((1+\alpha)^2M_2=\alpha^2M_1+(3\alpha^3+3\alpha^4+\alpha^5)M_1-\alpha^2M_1\)，

即\((1+\alpha)^2M_2=(3\alpha^3+3\alpha^4+\alpha^5)M_1\)，则\(\cfrac{M_2}{M_1}=\cfrac{3\alpha^3+3\alpha^4+\alpha^5}{(1+\alpha)^2}\)，

即\(\cfrac{M_2}{M_1}\approx 3\alpha^3\)，则\(\alpha^3\approx \cfrac{M_2}{3M_1}\)，

故\(\alpha\approx \sqrt[3]{\cfrac{M_2}{3M_1}}\)，即\(\cfrac{r}{R}\approx \sqrt[3]{\cfrac{M_2}{3M_1}}\)，则\(r\approx \sqrt[3]{\cfrac{M_2}{3M_1}}\cdot R\)，故选\(D\)。

【解后反思】

• 1、你怎么强化自己的阅读理解能力都不嫌过分；近似计算的思路分析过程要清楚；运算功底要扎实，到位。

• 2、\((1+\alpha)^3=1+3\alpha+3\alpha^2+\alpha^3\)；\((a\pm b)^3=a^3\mp 3a^2b\pm 3ab^2-b^3\)；

• 3、整个求解过程中的换元法的使用思路：

\(\cfrac{M_1}{(R+r)^2}+\cfrac{M_2}{r^2}=(R+r)\cfrac{M_1}{R^3}\) \(\xlongequal[同乘以R^2，变形]{为引入\alpha，便于近似计算}\)

\(\stackrel{\frac{r}{R}=>\alpha}{\Longrightarrow} \cfrac{M_1}{(1+\alpha)^2}+\cfrac{M_2}{\alpha^2}=(1+\alpha)M_1\)，

整理变形，得到\(\alpha\approx \sqrt[3]{\cfrac{M_2}{3M_1}}\)， \(\stackrel{\alpha=>\frac{r}{R}}{\Longrightarrow} \cfrac{r}{R}\approx \sqrt[3]{\cfrac{M_2}{3M_1}}\)，

从而得到，\(r\approx \sqrt[3]{\cfrac{M_2}{3M_1}}\cdot R\)，故选\(D\)。

• 4、该题目到底是数学题目还是物理题目？

当你将本题目的物理知识背景都去掉，抽象为“已知公式：\(\cfrac{M_1}{(R+r)^2}+\cfrac{M_2}{r^2}=(R+r)\cfrac{M_1}{R^3}\)，且已知\(\alpha=\cfrac{r}{R}\)，\(\cfrac{3\alpha^3+3\alpha^4+\alpha^5}{(1+\alpha)^2}\approx 3\alpha^3\)，试用\(M_1\)，\(M_2\)，\(R\)表示\(r\)的近似值”，那么此时的题目就是纯粹的数学题目，当添加上物理知识背景后，既可以看成物理题，也可以看成数学题，由此我们还能感悟得到，数学这门学科应该是物理、化学、生物等学科的工具学科，当其他具体学科中的问题转化建立了数学模型后，剩下的求解就是纯粹的数学知识了。

我们的问题：不清楚化简的方向，不清楚化简的方法。

【2018年全国卷Ⅱ卷理科数学解析[陕]】函数\(f(x)=\cfrac{e^x-e^{-x}}{x^2}\)图像大致是【】。

【分析】本题目考查函数图像的辨析，需要利用函数的性质求解，函数的性质常包含定义域、值域、单调性、奇偶性、周期性、对称性、特殊值、驻点等等，具体要用到哪些性质往往因题目而异。

法1：由题目先分析函数的奇偶性，设\(g(x)=e^x-e^{-x}\)，则\(g(-x)=e^{-x}-e^x=-g(x)\)，即函数\(g(x)\)为奇函数，又函数\(y=x^2\)为偶函数，故函数\(f(x)\)为奇函数，排除选项A；再由特殊值法，令\(x=3\)，则估算\(f(3)=\cfrac{e^3-e^{-3}}{3^2}\approx\cfrac{2.7^3}{3^2}\approx 2\)，排除C、D；故选B。

法2：还可以利用奇偶性和单调性来解析本题目，奇偶性如上所述；单调性，\(f'(x)=\cfrac{(e^x+e^{-x})x^2-(e^x-e^{-x})\cdot 2x}{(x^2)^2}=\cfrac{(x-2)e^x+(x+2)e^{-x}}{x^3}\)，接下来常规方法是判断其在\(x>0\)时的准确的单调区间，这时候不但麻烦，而且已经将题目变成了做函数图像的方法了，不是辨析函数图像的方法，
此时我们观察可以看到当\(x>2\)时，\(f'(x)>0\)，故函数\(f(x)\)在\((2，+\infty)\)上单调递增，故排除C和D，从而选B。

反思：1、弄清楚题目的类型和相应的解法思路是非常必要的。

2、函数的奇偶性的判断中，有一个常用的方法就是利用性质，比如 奇+奇=奇，奇\(\times\)奇=偶，奇\(\times\)偶=奇，奇/偶=奇，这些常见的结论一般的高三复习资料上都会有的。

建议：常见函数的奇偶性需要记忆比如，\(f(x)=|x|\)，\(f(x)=e^x+e^{-x}\)，\(f(x)=Acos\omega x\)都是偶函数；\(y=x^3\)，\(y=e^x-e^{-x}\)，\(y=Asin\omega x\)都是奇函数。

已知\(\Delta ABC\)中，\(sin(A-\cfrac{\pi}{4})=\cfrac{7\sqrt{2}}{26}\)，若\(\Delta ABC\)的面积为24，\(c=13\)，求\(a\)的值。

分析：由\(sin(A-\cfrac{\pi}{4})=\cfrac{7\sqrt{2}}{26}\)，估算\(A\)为锐角，打开整理得到\(sinA-cosA=\cfrac{7}{13}\)，

结合勾股数\(5，12，13\)可知，\(sinA=\cfrac{12}{13}，cosA=\cfrac{5}{13}\)，

由\(S_{\Delta}=\cfrac{1}{2}bcsinA=\cfrac{1}{2}\times b\times 13\times\cfrac{12}{13}=24\)，解得\(b=4\)，

由余弦定理可得\(a^2=b^2+c^2-2bccosA=16+169-2\times 4\times 13 \times \cfrac{5}{13}=145\)，

故\(a=\sqrt{145}\).

【2019年高考数学试卷理科新课标Ⅱ第13题】我国高铁发展迅速，技术先进。经统计，在经停某站的高铁列车中，有\(10\)个车次的正点率为\(0.97\)，有\(20\)个车次的正点率为\(0.98\)，有\(10\)个车次的正点率为\(0.99\)，则经停该站高铁列车所有车次的平均正点率的估计值为____________.

分析：由题目可知，经停该站高铁列车所有车次为\(40\)个车次，那么利用加权平均数的计算公式就可以求解平均值。

解析：\(\bar{x}=\cfrac{10}{40}\times 0.97+\cfrac{20}{40}\times 0.98+\cfrac{10}{40}\times 0.99=0.98\).

解后反思：听学生反馈，说是题目理解有误，他弄不清楚正点率为\(0.98\)的\(20\)个车次里面，到底是不是包含了开始说的那\(10\)个车次，很明显是不包含的，故正确、准确理解题意很关键。

【2019年高考数学试卷理科新课标Ⅱ第20题】已知函数\(f(x)=lnx-\cfrac{x+1}{x-1}\)，利用零点存在性定理判断函数在\((1，+\infty)\)内是否有零点时，用赋值法估算\(f(e)\)和\(f(e^2)\)的值；

解析：\(f(e)=1-\cfrac{e+1}{e-1}<0\)，\(f(e^2)=2-\cfrac{e^2+1}{e^2-1}=\cfrac{e^2-3}{e^2-1}>0\)，所以\(f(x)\)在\((1，+\infty)\)内有唯一的零点\(x_1\)，即\(f(x_1)=0\)；

采用系统抽样方法从\(960\)人中抽取\(32\)人做问卷调查，为此将他们随机编号为\(1\)，\(2\)，\(\cdots\)，\(960\)，分组后在第一组采用简单随机抽样的方法抽到的号码为\(9\)，抽到的\(32\)人中，编号落入区间\([1,450]\)的人做问卷\(A\)，编号落入区间\([451，750]\)的人做问卷\(B\)，其余的人做问卷\(C\)，则抽到的人中，做问卷\(B\)的人数为【\(\quad\)】

$A.7$ $B.9$ $C.10$ $D.15$

分析：形成一个首项为\(9\)，公差为\(30\)的等差数列，由\(9+(n-1)\times 30=450\)，

解得\(n\approx 15.7\)，再用\(n=15\)代入确认，\(9+(15-1)\times 30=429\)，

故在第一组中有\(15\)个人，第二组的第一个号码为\(429+30=459\)，

再用同样的思路求解第二组的人数有\(10\)个，故第三组的人数有\(7\)个。

设\(p: f(x)=e^{x}+\ln x+2x^{2}+mx+1\)在\((0,+\infty)\)内单调递增，\(q:m\geqslant -5\)，则\(p\)是\(q\)的【\(\quad\)】

$A.$必要不充分条件

$B.$充分不必要条件

$C.$充分必要条件

$D.$既不充分也不必要条件

解析：对于命题\(p: f(x)=e^{x}+\ln x+2x^{2}+m x+1\) 在\((0,+\infty)\)内单调递增，

则\(f^{\prime}(x)=e^{x}+\cfrac{1}{x}+4x+m\geqslant 0\)在\((0,+\infty)\)内恒成立，

分离参数，得到\(m\geqslant -e^{x}-\cfrac{1}{x}-4x\)在\((0,+\infty)\)上恒成立，

令\(g(x)=-e^{x}-\cfrac{1}{x}-4x=-(e^{x}+4x+\cfrac{1}{x})\)，

由于\(x>0\)，则\(e^{x}>1\)，又\(4x+\cfrac{1}{x} \geqslant 2\sqrt{4x\cdot\cfrac{1}{x}}=4\)，

则\(e^{x}+4 x+\cfrac{1}{x}>5\)，说明此处，两个同向不等式相加，由于其中一个不能取到等号，故结果不能取到等号\(\quad\)，则\(g(x)<-5\)，

设\(g(x)\)的最大值为\(N\)[比如取为\(-5.5\)]，则必有\(N<-5\)，

则化简命题\(p\)后得到参数的取值范围是\(m\geqslant N[-5.5]\)，所以\(p\)是\(q\)的必要不充分条件，故选\(A\).

【2021届宝鸡市一检文科数学第12题】 直线 \(y=ax+c\) 与曲线 \(y=e^{x}\) 相切于点 \((x_{0}, e^{x_{0}})\) ，且 \(x_{0}\in[0,1]\)，设 \(b=\log _{5}(3^{a}+4^{a})\)， 则 \(a\) 与 \(b\) 的大小关系是 【\(\quad\)】

$A.a=b$ $B.a > b$ $C.a < b$ $D.以上均有可能$

解析：由直线 \(y=ax+c\) 与曲线 \(y=e^{x}\) 相切于点 \((x_{0}, e^{x_{0}})\)可知 ，则切线斜率为 \(k=a\) 且 \(k=e^{x_0}\)，

则\(a=e^{x_0}\)，又由于\(x_{0}\in[0,1]\)，故\(a\in [1,e]\)，问题转换为：

当 \(a\in [1,e]\) 时，比较 \(b=\log _{5}(3^{a}+4^{a})\) 与 \(a\)的大小关系；

注意到 \(b\) 为对数式，故想到将 \(a\) 对数化为 \(a=log_55^a\)，

比较\(b=\log _{5}(3^{a}+4^{a})\) 与 \(a=log_55^a\) 的大小，这样只需要比较 \(3^a+4^a\) 与 \(5^a\) 的大小关系，

注意到，\(3^2+4^2=5^2\)，我们想到需要针对 \(a\) 分类讨论，可以使用验证法；

当\(a=1\)时，\(3^1+4^1>5^1\)，故\(b>a\)；

当\(a=2\)时，\(3^2+4^2=5^2\)，故\(b=a\)；

当\(a=\cfrac{5}{2}\)时，\(3^{\frac{5}{2}}+4^{\frac{5}{2}}\approx48.2\)，\(5^{\frac{5}{2}}=25\sqrt{5}\approx57.5\)，故\(b<a\)；

故选\(D\)；

补充：①\(7\leqslant 3^a+4^a\leqslant 3^e+4^e\)，\(5\leqslant 5^a\leqslant 5^e\)；

②\(\cfrac{3^a+4^a}{5^a}=(\cfrac{3}{5})^a+(\cfrac{4}{5})^a\)； \(\cos\theta\)，\(\sin\theta\)；

③证明，若\(n\geqslant 3，n\in N^*\)，则\(3^n+4^n<5^n\)；

【2021届宝鸡市一检理科数学第12题】 设 \(1<a<2\)， \(m=\log _{4}(2^{a}+3^{a})\)， \(n=\log _{5}(3^{m}+4^{m})\)， 则 【\(\quad\)】

$A.n=2$ $B.n >2$ $C.n <2$ $D.以上均有可能$

法1： 不等式性质法，因为 \(1<a<2\)， 所以 \(5<2^{a}+3^{a}<13\)，

所以 \(1<\log_{4}5<m<\log_{4}13<2\)，

所以 \(1<m<2\)， 所以 \(7<3^{m}+4^{m}<25\)，

所以 \(1<\log _{5}7<n<\log _{5}25=2\)

所以 \(n<2\)， 故选 \(C\) .

法2：估值计算法，

令\(a=\cfrac{3}{2}\)，\(2^{\frac{3}{2}}+3^{\frac{3}{2}}=2\sqrt{2}+3\sqrt{2}=5\sqrt{2}=\sqrt{50}=7\)

\(m=log_47\approx log_48=\cfrac{3}{2}log_22=\cfrac{3}{2}\)；

当\(m=\cfrac{3}{2}\)时，\(3^{\frac{3}{2}}+4^{\frac{3}{2}}\approx 13.2\)，

\(n=\log _{5}(3^{m}+4^{m})=\log_513.2<\log_5 25=2\)，故\(n<2\)，故选 \(C\) ；

【2021届宝鸡市一检文科数学第4题】 很多关于大数的故事里（例如“棋盘上的学问”，“64片金片在三根金针上移动的寓言”) 都涉及 \(2^{64}\) 这个数. 请你估算这个数 \(2^{64}\) 大致所在的范围是 【\(\quad\)】(参考数据: \(\lg2\)\(\approx\)\(0.30\)， \(\lg3\)\(\approx\)\(0.48\))

$A.(10^{12}, 10^{13})$ $B.(10^{19}, 10^{20})$ $C.(10^{20}, 10^{21})$ $D.(10^{30}, 10^{31})$

分析：设\(a<2^{64}<b\)，则\(lga<64\cdot lg2<lgb\)，即\(lga<19.2<lgb\)，

若是选项 \(A\)，则\(a=10^{12}\)，\(b=10^{13}\)，则\(12<19.2<13\)，故\(A\)错误；同理排除选项 \(C\)，\(D\)，故选\(B\)；

从折线图中估算平均数和方差、标准差等，

【2020-江西九江一中质检】我国古代数学名著《九章算术》中“开立圆术”曰：置积尺数，以十六乘之，九而一，所得开立方除之，即立圆径。“开立圆术”相当于给出了已知球的体积 \(V\)， 求其直径 \(d\) 的一个近似公式 \(d\)\(\approx\)\(\sqrt[3]{\frac{16}{9} V}\) . 人们还用过一些类似的近似公式，根据 \(\pi=3.14159...\)判断，下列近似公式中最精确的一个是【\(\quad\)】

$A.d\approx\sqrt[3]{2V}$ $B.d\approx\sqrt[3]{\frac{21}{11} V}$ $C.d\approx\sqrt[3]{\frac{16}{9} V}$ $D.d\approx\sqrt[3]{\frac{300}{157} V}$

法1： 由球的体积公式可得 \(V=\cfrac{4}{3}\pi R^3=\cfrac{4}{3}\pi(\cfrac{d}{2})^3\)，故 \(d=\sqrt[3]{\frac{6}{\pi}V}\)，

设每个选项中的 \(V\) 前面的常数系数为 \(\cfrac{a}{b}\)，则有 \(\cfrac{6}{\pi}=\cfrac{a}{b}\)，则 \(\pi=\cfrac{6b}{a}\)，

在选项 \(A\) 中，代入得 \(\pi=\cfrac{6}{2}=3\)；

在选项 \(B\) 中，代入得 \(\pi=\cfrac{11\times 6}{21}\approx 3.142857\)；

在选项 \(C\) 中，代入得 \(\pi=\cfrac{6\times9}{16}= 3.375\)；

在选项 \(D\) 中，代入得 \(\pi=\cfrac{6\times 157}{300}=3.14\)；

由于选项 \(B\) 中的值最接近 \(\pi\) 的真实值，故选 \(B\).

法2：由于 \(d=\sqrt[3]{\frac{6}{\pi}V}\)，计算得到的是 \(d\) 的真实值，故选项中哪个常数系数最接近 \(\cfrac{6}{\pi}\)，哪个就是最接近真实值的；

又由于 \(\cfrac{6}{\pi}\approx 1.90985\)； \(\cfrac{21}{11}\approx 1.90909\) ； \(\cfrac{16}{9}\approx 1.77777\) ；\(\cfrac{300}{157}\approx 1.91082\) ；

相比较，故选\(B\)；

【2020·聊城模拟】足球运动是一项古老的体育活动，众多的资料表明，中国古代足球的出现比欧洲早，历史更为悠久，如图，现代比赛用的足球是由正五边形与正六边形构成的共32个面的多面体。

著名数学家欧拉证明了凸多面体的面数( \(F\) )，顶点数( \(V\) )，棱数 (\(E\)) 满足\(F+V-E=2\)，那么，足球有______个正六边形的面，若正六边形的边长为\(\sqrt{21}\)，则足球的直径为________ \(cm\) (结果保留整数）（参考数据：\(\tan54^{\circ}\approx1.38\)，\(\sqrt{3}\approx 1.73\)， \(\pi\approx 3.14\)）.

解析：因为足球是由正五边形与正六边形构成，所以每块正五边形皮料周围都是正六边形皮料，每两个相邻的多边形恰有一条公共边，每个顶点处都有三块皮料，而且都遵循一个正五边形，两个正六边形的构造。

设正五边形为 \(x\) 块，正六边形为 \(y\) 块，则凸多面体的面数 \(F=x+y=32\) ，且凸多面体的顶点数 \(V=\cfrac{1}{3}(5x+6y)\)，凸多面体的棱数 \(E=\cfrac{1}{2}(5x+6y)\)，

故得到方程组 \(\left\{\begin{array}{l}{x+y=32}\\{(x+y)+[\cfrac{1}{3}(5x+6y)]-[\cfrac{1}{2}(5x+6y)]=2}\end{array}\right.\)

解得， \(x=12\)，\(y=20\)， 即足球有 \(12\) 个正五边形的面，有 \(20\) 个正六边形的面；

每个正六边形[可以等分为六个等面积的正三角形]的面积为 \([\cfrac{1}{2}\times(\sqrt{21})^{2}\times\cfrac{\sqrt{3}}{2}]\times6=\cfrac{63\sqrt{3}}{2}\)，

每个正五边形[可以等分为五个等面积的等腰三角形]的面积为 \(\cfrac{1}{2}\times\sqrt{21}\times\cfrac{\sqrt{21}\times\tan 54^{\circ}}{2}\times 5=\cfrac{105 \tan54^{\circ}}{4}\)，

故足球的表面积为 \(S=20\times\cfrac{63\sqrt{3}}{2}+12\times\cfrac{105\tan 54^{\circ}}{4}=630\sqrt{3}+315\tan 54^{\circ}\)，

\(\approx 1089.9+434.7=1524.6\)

所以 \(4 \pi R^{2}=\pi(2 R)^{2}=1524.6, \quad 2 R \approx 22\).

所以足球的直径为 \(22\) .

本题目补充：凸 \(n\) 边形的内角和公式：\((n-2)\cdot 180^{\circ}\)；

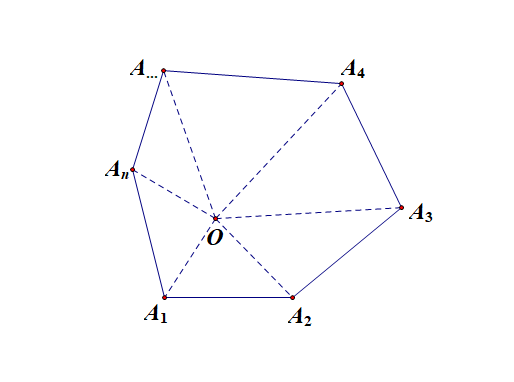
证明： 在凸 \(n\) 边形的内部任取一点\(O\)，分别连接点 \(O\) 和凸 \(n\) 边形的各个顶点，我们得到了 \(n\) 个三角形，则凸 \(n\) 边形的内角之和等于 \(n\) 个三角形的内角和，再减去围绕点 \(O\) 形成的周角，即\(n\cdot 180^{\circ}-2\cdot 180^{\circ}=(n-2)\cdot 180^{\circ}\).

故正五边形的内角为 \(108^{\circ}\) ，其一半为 \(54^{\circ}\).

【2022届高三数学三轮模拟冲刺用题】高德纳箭头表示法是一种用来表示很大的整数的方法， 它的理念来自乘法是重复的加法，幂是重复的乘法。 定义： \(a\uparrow b=\underbrace{a\cdot a\cdot a\cdot\ldots\cdot a}_{ b 个 a}=a^{b}\)， \(a\uparrow\uparrow b=\underbrace{a\uparrow a\uparrow a\uparrow\ldots\uparrow a}_{ b 个 a}\) (从右往左计算)。 已知可观测宇宙中普通物质的原子总数 \(T\) 约为 \(10^{82}\)， 则下列各数中与 \(\cfrac{4\uparrow\uparrow 3}{T}\) 最接近的是 (参考数据: \(\lg2\approx 0.3\) )【\(\qquad\)】

$A.10^{-64}$ $B.10^{-64}$ $C.10^{71}$ $D.10^{74}$

解析：由定义可知， \(4\uparrow\uparrow3=4\uparrow 4\uparrow4=4\uparrow(4\uparrow 4)=4^{4\uparrow4}=4^{4^4}=4^{256}\)，

则 \(\lg\cfrac{4\uparrow\uparrow 3}{T}=\lg\cfrac{4^{256}}{10^{82}}=256\lg4-82\lg{10}=512\lg2-82\approx 71.6\)，

故 \(\cfrac{4\uparrow\uparrow 3}{T}\approx 10^{71.6}\Rightarrow 10^{71}\)，故选 \(C\) .

【2022届高三数学三轮模拟冲刺用题】数列 \(H_{n}=1+\cfrac{1}{2}+\cfrac{1}{3}+\cdots+\cfrac{1}{n}\) 通常被称为 “调和级数”， 是级数理论中最早被人们研究的级数之一， 著名数学家欧拉在 \(1734\) 年就曾给出证明： 当 \(n\) 足够大时, \(H_{n}\approx\ln(n+1)+\gamma\), 其中 \(\gamma\) 为欧拉一马歇罗尼常数， 其值约为 \(0.57\)， 在本题的计算中可以忽略不计。 据此， \(H_{511}\) 与 \(H_{99}\) 之比的近似值为(参考数据: \(\lg2\approx 0.3\) ) 【\(\qquad\)】

$A.1.50$ $B.1.35$ $C.1.20$ $D.1.05$

解析：由题目定义以及约定可知，

\(\cfrac{H_{511}}{H_{99}}=\cfrac{\ln512}{\ln100}=\cfrac{9\ln2}{2\ln{10}}=\cfrac{9}{2}\times \cfrac{\ln2}{\ln{10}}=\cfrac{9}{2}\times\lg2=1.35\)，故选 \(B\) .