求曲线的轨迹方程

前言

注意事项

求轨迹和求轨迹方程是不一样的，求轨迹方程只需要写出其方程即可，若是求轨迹，除过写出方程外，还需要说明轨迹的样子，比如圆需要说明圆心和半径，椭圆需要说明中心和长轴与短轴等。

常见方法

直接法

若曲线上的动点满足的条件是一些几何量的等量关系，则只需要直接将这种关系“翻译成”动点的坐标$(x，y)$的方程，经化简所得同解的最简方程，即为所求轨迹的方程，其一般步骤为：建系$\Rightarrow$设点$\Rightarrow$列式$\Rightarrow$代换$\Rightarrow$化简$\Rightarrow$检验。

定义法

若动点的轨迹的条件符合某一基本轨迹的定义，如圆、椭圆、双曲线、抛物线的定义，则可以直接根据定义求出动点的轨迹方程。近年考试常常和圆锥曲线的定义结合很紧密，故需要特别注意。

待定系数法

当已知动点的轨迹是某种圆锥曲线，则可设出含有待定系数的方程，再根据动点满足的条件，确定待定系数，从而求得动点的轨迹方程。

相关点法[代入法]

将未知曲线上的动点坐标$P(x，y)$用已知曲线上的动点坐标$P_0(x_0，y_0)$表示，反解得到$x_0=f(x)$，$y_0=g(y)$，然后将其代入已知曲线方程中，整理得到的方程即为待求曲线的轨迹方程，这一方法就叫相关点法，也叫代入法。

参数法

如果轨迹动点$P(x，y)$的坐标之间的关系不易找到，也没有相关的点可用时，可先考虑将$x$，$y$用一个或者几个参数来表示，然后消去参数可得到轨迹方程，此法称为参数法，用参数法求轨迹方程需要注意参数的范围对方程的影响。

以坐标原点$O$为极点，$x$轴的正半轴为极轴建立极坐标系，已知曲线$C$的极坐标方程为$\rho=4cos\theta$，曲线$M$的直角坐标方程为$x-2y+2=0(x>0)$，以曲线$M$上的点与点$O$连线的斜率为参数，写出曲线$M$的参数方程；

分析：由$\left\{\begin{array}{l}{x-2y+2=0(x>0)①}\\{y=kx②}\end{array}\right.$

解方程，消去$y$，解得$x=\cfrac{2}{2k-1}$，代入②得到，$y=\cfrac{2k}{2k-1}$，由$x=\cfrac{2}{2k-1}>0$，得到$k>\cfrac{1}{2}$

故曲线$M$的参数方程为$\left\{\begin{array}{l}{x=\cfrac{2}{2k-1}}\\{y=\cfrac{2k}{2k-1}}\end{array}\right.$ ($k$为参数，$k>\cfrac{1}{2}$)

点差法

涉及到中点坐标有关的问题求轨迹方程，可以考虑用点差法；

交轨法

交轨法是解析几何中求动点轨迹方程的常用方法之一。首先选择适当的参数表示两动曲线的方程，将两动曲线方程中的参数消去，然后得到不含参数的方程，此方程即为两动曲线交点的轨迹方程，这种求轨迹方程的方法叫做交轨法[交点轨迹法]。

求两条直线$x-my-1=0$和$mx+y-1=0$的交点的轨迹方程。

法1：参数方程法，首先联立两个方程，得到$\left\{\begin{array}{l}{x-my-1=0①}\\{mx+y-1=0②}\end{array}\right.$

给②式乘以$m$，消$y$得到，$x=\cfrac{m+1}{m^2+1}$，代入②式得到$y=\cfrac{1-m}{m^2+1}$

即交点轨迹的参数方程为

\[\left\{\begin{array}{l}{x=\cfrac{m+1}{m^2+1}}\\{y=\cfrac{1-m}{m^2+1}}\end{array}\right.\quad (m为参数) \]

或者说我们就可以用参数方法来回答这个问题。

不过我们还是继续完成接下来的任务，重点和难点是消参。

$\left\{\begin{array}{l}{x=\cfrac{m+1}{m^2+1}①}\\{y=\cfrac{1-m}{m^2+1}②}\end{array}\right.\quad (m为参数)$，如何消参，

给 $①^2$ + $②^2$，得到 $x^2+y^2=\cfrac{(m+1)^2}{(m^2+1)^2}+\cfrac{(1-m)^2}{(m^2+1)^2}=\cfrac{2}{m^2+1}$，

又$x+y=\cfrac{2}{m^2+1}$，故$x^2+y^2-x-y=0$。

又当$x=0$且$y=0$时，$m$不存在，

故所求的轨迹方程为$x^2+y^2-x-y=0(x\neq0且y\neq 0)$。

法2：交轨法，将两个方程分别变形为$my=x-1$和$mx=1-y$，

当$m=0$时，两个方程不能相除，此时得到两个直线的交点为$(1，1)$；

当$m\neq 0$时，两式相除得到$\cfrac{my}{mx}=\cfrac{x-1}{1-y}$，即$\cfrac{y}{x}=\cfrac{x-1}{1-y}$，

变形为$y(1-y)=x^2-x$，整理为$x^2+y^2-x-y=0$，即$(x-\frac{1}{2})^2+(y-\frac{1}{2})^2=\cfrac{1}{2}$

再分别验证点$(1，1)$和点$(0，1)$和点$(1，0)$都在上述曲线上，但是点$(0，0)$不应该在轨迹曲线上，

[为什么验证这四个点，原因是由$\cfrac{y}{x}=\cfrac{x-1}{1-y}$，两个横行即分子分母都为零，得到点$(0，1)$和$(1，0)$，两个竖行都为零，得到点点$(0，0)$和$(1，1)$，]

故所求的轨迹方程为$x^2+y^2-x-y=0(x\neq0且y\neq 0)$。

特殊化策略

个别涉及选择类型题目的轨迹方程的求法，可以使用特殊化策略。

典例剖析

【直接法】【2019年高考数学试卷理科新课标Ⅱ第21题】已知点$A(-2，0)$，$B(-2，0)$，动点$M(x，y)$满足直线$AM$与$BM$的斜率之积为$-\cfrac{1}{2}$，记$M$的轨迹为曲线$C$。

(1).求$C$的方程，并说明$C$是什么曲线；

分析：本题目可以用直接法得到曲线的方程，难点是要注意到不是恒等变形，需要添加条件。

解析：由于$k_{AM}=\cfrac{y}{x+2}$，$k_{BM}=\cfrac{y}{x-2}$，由题可知，$k_{AM}\cdot k_{BM}=-\cfrac{1}{2}$，

化简得到$x^2+2y^2=4$，再整理为$\cfrac{x^2}{4}+\cfrac{y^2}{2}=1$，

[此时，务必要注意，我们是将分式形式转化为整式形式，这一过程有去分母的变形，一定会扩大字母的取值范围，故需要添加条件才能保证变形前后是恒等变形，以此题为例，由于有分母，故需要$|x|\neq 2$，或者对应到$y$值加以限制也是可以的，比如$y\neq 0$]，

即曲线$C$的方程为$\cfrac{x^2}{4}+\cfrac{y^2}{2}=1(|x|\neq 2)$，或者$\cfrac{x^2}{4}+\cfrac{y^2}{2}=1(y\neq 0)$，所以$C$为中心在坐标原点，焦点在$x$轴上的椭圆，且不含左右顶点。

【定义法】已知圆$M：(x+1)^2+y^2=1$，圆$N：(x-1)^2+y^2=9$，动圆$P$与圆$M$外切并且与圆$N$内切，圆心$P$的轨迹方程为曲线$C$。

(1)、求$C$的方程；

分析：由已知得，圆$M$的圆心为$M(-1，0)$，半径$r_1=1$；

圆$N$的圆心为$N(1，0)$，半径$r_2=3$；

设圆$P$的圆心为$P(x，y)$，半径为$R$；

由于圆$P$与圆$M$外切并且与圆$N$内切，

所以$|PM|+|PN|=(R+r_1)+(r_2-R)=r_1+r_2=4$，

由[椭圆的定义]可知，曲线$C$是以$M$，$N$为左右焦点，长半轴长为2，短半轴长为$\sqrt{3}$的椭圆(左顶点除外)，

其轨迹方程为$\cfrac{x^2}{4}+\cfrac{y^2}{3}=1(x\neq -2)$。

(2)、$l$是与圆$P$，圆$M$都相切的一条直线，$l$与曲线$C$交于$A$，$B$两点，当圆$P$的半径最长时，求$|AB|$；

待整理。

【点差法】已知椭圆$\cfrac{x^2}{2}+y^2=1$，求斜率为$2$的平行弦的中点的轨迹方程。

解：设弦的两个端点分别为$P(x_1，y_1)，Q(x_2，y_2)$，$PQ$的中点为$M(x，y)$，

则有$\cfrac{x_1^2}{2}+y_1^2=1$①，$\cfrac{x_2^2}{2}+y_2^2=1$②，

①-②得到，$\cfrac{x_1^2-x_2^2}{2}+y_1^2-y_2^2=0$

则有$\cfrac{x_1+x_2}{2}+\cfrac{y_1-y_2}{x_1-x_2}(y_1+y_2)=0$

又由于$x_1+x_2=2x$，$y_1+y_2=2y$，$\cfrac{y_1-y_2}{x_1-x_2}=k=2$，

代入上式，得到$x+4y=0$，

又由于弦中点在椭圆内，故所求的弦中点的轨迹方程为$x+4y=0$(在已知椭圆内)。

【参数方程法】已知过原点的动直线$l$与圆$C_1：x^2+y^2-6x+5=0$相交于不同的两点$A，B$，

(1)、求直线$l$的斜率$k$的取值范围；

分析：圆的标准方程为$(x-3)^2+y^2=2^2$，

故圆心坐标$C_1(3，0)$，半径为$r=2$，

设直线$l$的方程为$y=kx$，即$kx-y=0$，

则圆心$C_1$到直线$l$的距离$d=\cfrac{|3k|}{\sqrt{k^2+1}}< 2$，

解得$-\cfrac{2\sqrt{5}}{5}< k< \cfrac{2\sqrt{5}}{5}$；

(2)、求线段$AB$的中点$M$的轨迹$C$的方程。

分析【法1】：设直线$AB$的方程为$y=kx$，点$A(x_1，y_1)$，$B(x_2，y_2)$

与圆$C_1$联立，消$y$得到，$(1+k^2)x^2-6x+5=0$，

由$\Delta =(-6)^2-4\times 5(1+k^2)>0$，可得$k^2<\cfrac{4}{5}$，

由韦达定理可得，$x_1+x_2=\cfrac{6}{1+k^2}$，

则线段$AB$的中点$M$的轨迹$C$的参数方程为$\left\{\begin{array}{l}{x=\cfrac{3}{1+k^2}①}\\{y=\cfrac{3k}{1+k^2}②}\end{array}\right.$，其中$-\cfrac{2\sqrt{5}}{5}<k<\cfrac{2\sqrt{5}}{5}$，

如何消参数呢？两式相比，得到$y=kx$，即$k=\cfrac{y}{x}$，

代入①变形整理后得到，$(x-\cfrac{3}{2})^2+y^2=\cfrac{9}{4}$，

又由于$k^2<\cfrac{4}{5}$，得到$\cfrac{5}{3}<x\leq 3$，

故线段$AB$的中点$M$的轨迹$C$的方程为$(x-\cfrac{3}{2})^2+y^2=\cfrac{9}{4}$，其中$\cfrac{5}{3}<x\leq 3$。

【法2】有空，再思考补充点差法。

思路补记：$(x_1+x_2)[(x_1-x_2)-6]=-(y_1+y_2)(y_1-y_2)$。

【相关点法】在直角坐标系$xoy$中，以坐标原点为极点，$x$轴正半轴为极轴建立极坐标系，曲线$C_1$的方程为$\rho(\rho-4sin\theta)=12$，定点$A(6，0)$，点$P$是$C_1$上的动点，$Q$为$AP$的中点，求点$Q$的轨迹$C_2$的直角坐标方程；

分析：将曲线$C_1$的极坐标方程化为直角坐标方程为$x^2+y^2-4y=12$，

设点$P(x'，y')$，点$Q(x，y)$，由$Q$为$AP$的中点，得到$\begin{cases}x'=2x-6\\y'=2y\end{cases}$，

代入$x^2+y^2-4y=12$，

得到点$Q$的轨迹$C_2$的直角坐标方程为$(x-3)^2+(y-1)^2=4$；

平面直角坐标系$xoy$中，若动圆与圆$(x-2)^2+y^2=1$外切，且又与直线$x+1=0$相切，则动圆圆心的轨迹方程为【】

$A.y^2=8x$ $B.x^2=8y$ $C.y^2=4x$ $D.x^2=4y$

法1：直接法，如图所示，动圆的圆心为点$P(x,y)$，则有$|PN|=|PM|+1$，

即$\sqrt{(x-2)^2+(y-0)^2}=|x+1|+1$，由于动圆在直线$x+1=0$的右侧，即$x+1>0$，

故化简得到$\sqrt{(x-2)^2+(y-0)^2}=x+1+1$，整理得到$y^2=8x$，故选$A$；

法2：定义法，转化为能利用抛物线的定义来求解，其定义是说动点到定点的距离等于其到定直线的距离，

这样定点取$(2，0)$，此时定直线必须取$x=-2$，

这样抛物线的标准方程为$y^2=2px(p>0)$，且$\cfrac{p}{2}=2$，即$p=4$，

故抛物线的标准方程为$y^2=8x$，故选$A$。

【2019届宝鸡市高三理科数学质检Ⅰ第8题】平面直角坐标系$xoy$中，动点$P$与圆$(x-2)^2+y^2=1$上的点的最短距离与其到直线$x=-1$的距离相等，则点$P$的轨迹方程为【】

$A.y^2=8x$ $B.x^2=8y$ $C.y^2=4x$ $D.x^2=4y$

分析：由题意可知，$|PQ|=|PD|$，但是用这个不好建立轨迹方程，或者不能有效的和抛物线的定义建立联系，

故等价转化为$|PA|=|PB|$，且其模型为$y^2=2px$。

这样就可以理解为平面内一个动点$P$到一个定点$A$的距离等于其到定直线$x=-2$的距离。

由抛物线的定义可知，$-\cfrac{p}{2}=-2$，即$p=4$，故$y^2=2\times 4x=8x$，故选$A$。

注意：抛物线的定义是高考考查时的高频考点。

已知点 $Q$ 在椭圆 $\cfrac{x^2}{16}+\cfrac{y^2}{10}=1$ 上，点 $P$ 满足 $\overrightarrow{OP}$$=$$\cfrac{1}{2}(\overrightarrow{OF_1}$$+$$\overrightarrow{OQ})$(其中 $O$ 为坐标原点，$F_1$ 为椭圆 $C$ 的左焦点)，求点 $P$ 的轨迹方程。

提示：设点$P(x，y)$，点$Q(x_1，y_1)$，点$F_1(-\sqrt{6}，0)$，

由$\overrightarrow{OP}=\cfrac{1}{2}(\overrightarrow{OF_1}+\overrightarrow{OQ})$，则可知点$P$为线段$F_1Q$的中点，

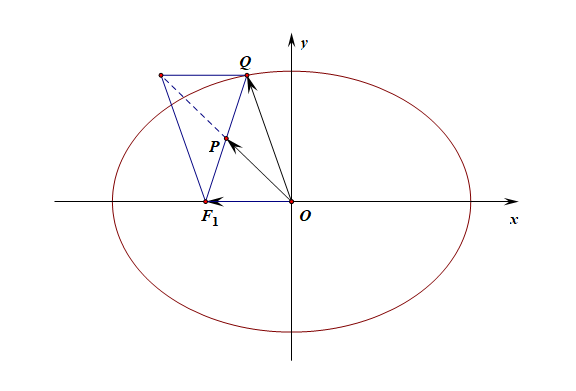
得到$\left\{\begin{array}{l}{2x=-\sqrt{6}+x_1}\\{2y=y_1,}\end{array}\right.\quad$，变形得到$\left\{\begin{array}{l}{x_1=2x+\sqrt{6}}\\{y_1=2y,}\end{array}\right.$

将其代入$\cfrac{x^2}{16}+\cfrac{y^2}{10}=1$，得到$\cfrac{(2x+\sqrt{6})^2}{16}+\cfrac{2y^2}{5}=1$.

即点$P$的轨迹方程为$\cfrac{(2x+\sqrt{6})^2}{16}+\cfrac{2y^2}{5}=1$。

【坐标法】在边长为 $2$ 的正 $\triangle ABC$ 中，若 $P$ 为 $\triangle ABC$ 内一点，且 $|PA|^{2}=|PB|^{2}+|PC|^{2}$，求点 $P$ 的轨迹方程，并画出方程所表示的曲线。

分析：本题目是曲线方程的确定与应用问题，考查建立平面直角坐标系、数形结合思想、曲线方程的求法及分析推理、计算化间技能、技巧等。解答需要先建立平面直角坐标系，写出各点的坐标，用直接法求解，再根据方程判定曲线类型画出其表示的曲线。

解析：以 $BC$ 所在直线为 $x$ 轴，$BC$ 的中点为原点，$BC$ 的中垂线为 $y$ 轴建立平面直角坐标系，

设 $P(x, y)$ 是轨迹上任意一点, 又 $|BC|=2$，故有 $B(-1,0)$， $C(1,0)$，则$A(0,\sqrt{3})$，

由于 $|PA|^{2}=|PB|^{2}+|PC|^{2}$，

即 $x^{2}+(y-\sqrt{3})^{2}=(x+1)^{2}+y^{2}+(x-1)^{2}+y^{2}$，

化简得到， $x^{2}+(y+\sqrt{3})^{2}=4$，

又由于点 $P$ 在 $\triangle ABC$ 内，所以 $y>0$，

所以， $P$ 点的轨迹方程为 $x^{2}+(y+\sqrt{3})^{2}=4(y>0)$.

其轨迹如图所示，为以 $(0,-\sqrt{3})$ 为圆心，半径为 $2$ 的圆在 $x$ 轴上方的圆弧.

【特殊化策略解决选择题】设椭圆$\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a>b>0)$上的动点$Q$，过动点$Q$做椭圆的切线$l$，过右焦点做$l$的垂线交$l$于点$P$，则点$P$的轨迹方程为【】

$A.x^2+y^2=a^2$ $B.x^2+y^2=b^2$ $C.x^2+y^2=c^2$ $D.x^2+y^2=e^2$

分析：由于点$Q$是椭圆上的任意一个动点，不妨取其在椭圆的四个特殊位置来思考；

当点$Q(a，0)$时，过动点$Q$做椭圆的切线$l：x=a$，过右焦点做$l$的垂线为$y=0$，则点$P(a，0)$，代入验证，只有选项$A$满足；

当点$Q(0，b)$时，过动点$Q$做椭圆的切线$l：y=b$，过右焦点做$l$的垂线为$x=c$，则点$P(c，b)$，代入验证，也只有选项$A$满足；

故用特殊化策略可知，选$A$。

解后反思：如果本题目直接求解，可能会很麻烦，由此也体现出特殊化策略在解选择题时的便捷性。

posted @ 2019-02-27 10:26 静雅斋数学阅读(1473) 评论(0) 编辑收藏举报

指间灵动，快码加编

刷新页面返回顶部

求曲线的轨迹方程

前言

相关概念

注意事项

常见方法

典例剖析

公告