$$ %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Self-defined math definitions %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Math symbol commands \newcommand{\intd}{\,{\rm d}} % Symbol 'd' used in integration, such as 'dx' \newcommand{\diff}{{\rm d}} % Symbol 'd' used in differentiation ... $$

决策树原理

1.特征选择

特征选择是选取对训练数据有分类能力的特征，常用的有信息增益（ information gain）、基尼不纯度（Gini impurity ）

信息增益（ information gain）

信息增益用在ID3、C4.5决策树生成算法中

wikipedia中信息增益的公式

{\displaystyle \overbrace {IG(T,a)} ^{\text{Information Gain}}=\overbrace {\mathrm {H} (T)} ^{\text{Entropy (parent)}}-\overbrace {\mathrm {H} (T|a)} ^{\text{Weighted Sum of Entropy (Children)}}}{\displaystyle =-\sum _{i=1}^{J}p_{i}\log _{2}{p_{i}}-\sum _{a}{p(a)\sum _{i=1}^{J}-\Pr(i|a)\log _{2}{\Pr(i|a)}}}
 
 J是分类数，几分类就是几
a是特征a的取值

Pr(i|a)是在a的属性下，第i个类别的概率

IG（T，a）是特征a对数据集T的信息增益

H（T）是数据集T的经验熵

H（T|a）是特征a给定条件下T的经验熵             

一个特征的信息增益越大，特征的分类能力越强

基尼不纯度（Gini impurity ）

基尼不纯度用在CART生成算法中

wikipedia中基尼不纯度的公式   

{\displaystyle \operatorname {I} _{G}(p)=\sum _{i=1}^{J}p_{i}\sum _{k\neq i}p_{k}=\sum _{i=1}^{J}p_{i}(1-p_{i})=\sum _{i=1}^{J}(p_{i}-{p_{i}}^{2})=\sum _{i=1}^{J}p_{i}-\sum _{i=1}^{J}{p_{i}}^{2}=1-\sum _{i=1}^{J}{p_{i}}^{2}}               

J是类别，pi是样本属于第i类的概率

特征A的基尼不纯度

 

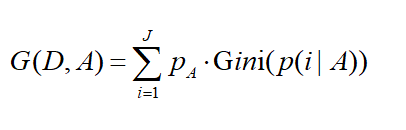
pA是特征A出现的概率，p(i|A)是在特征A的条件下，是类别i的概率

一个特征的基尼不纯度越小，特征分类能力越强

2. 决策树生成算法

常用决策树生成算法包括ID3、C4.5、CART

在scikit-learn中，使用的CART算法实现决策树

ID3算法

算法思想

1）计算所有特征的信息增益

2）选择信息增益最大的特征作为根节点

3）根据特征的取值建立子节点

4）重复步骤1-3，构建决策树

缺点

该算法是基于信息增益进行节点特征的选择，但该选择方法会倾向于属性值比较多的那些特征，易发生过拟合

不能处理连续的特征

C4.5算法

C4.5算法对ID3算法进行了改进，改进了以下几个方面

1）使用信息增益比来进行特征选择，使算法不偏向于选择属性值较多的特征

信息增益比的公式

splitInformation（D，A）是数据集D关于特征A的熵

g（D，A）是特征A的信息增益

2）创建了阈值用来处理连续属性，把连续的属性全部放进一个列表，对列表属性排序，根据阈值分割列表

注意，排序会降低C4.5算法的性能

3）对属性值丢失的情况，直接放弃该样本

 CART算法

算法思想

1）计算每个特征的基尼不纯度，选择基尼不纯度最小的作为最优切分点

2）比较每个特征的最优切分点，选择基尼不纯度最小的最优切分点，用它的特征作为最优特征，生成二叉树

3）二叉树的右边继续重复1,2，构建决策树

CART算法与ID3的最大不同：CART算法构造的是二叉树，二叉树精度通常高于多叉树

3. 决策树剪枝

预剪枝（ prepruning）

预剪枝是在决策树生成过程中，对树进行剪枝，提前结束树的分支生长。

优点：降低了过拟合风险，显著减少训练时间，测试时间

缺点：有可能导致欠拟合

预剪枝依据

1）作为叶结点或作为根结点需要含的最少样本个数

2）决策树的层数

3）结点的经验熵小于某个阈值才停止

后剪枝（postpruning）

后剪枝是在决策树生长完成之后，对树进行剪枝，得到简化版的决策树。

优点：欠拟合风险小，泛化性能通常高于预剪枝

缺点：训练时间比未剪枝和预剪枝大的多                                                                                                                                                                                                                                                                                          

posted @ 2018-12-21 16:53  V丶vvv  阅读(345)  评论(0)  编辑  收藏  举报