SVM学习——Improvements to Platt’s SMO Algorithm

纵观SMO算法，其核心是怎么选择每轮优化的两个拉格朗日乘子，标准的SMO算法是通过判断乘子是否违反原问题的KKT条件来选择待优化乘子的，这里可能有一个问题，回顾原问题的KKT条件：

$\alpha_i=0 \Leftrightarrow y_iu_i \geq 1$

$0 \leq \alpha_i \leq C \Leftrightarrow y_iu_i = 1$

$\alpha_i=C \Leftrightarrow y_iu_i \leq 1$

是否违反它，与这几个因素相关：拉格朗日乘子 $\alpha_i$ 、样本标记 $y_i$ 、偏置 $b$ 。 $b$ 的更新依赖于两个优化拉格朗日乘子，这就可能出现这种情况：拉格朗日乘子 $\alpha_i$ 已经能使目标函数达到最优，而SMO算法本身并不能确定当前由于两个优化拉格朗日乘子计算得到的 $b$ 是否就是使目标函数达到最优的那个 $b$ ，换句话说，对一些本来不违反KKT条件的点，由于上次迭代选择了不合适的 $b$ ，使得它们出现违反KKT条件的情况，导致后续出现一些耗时而无用的搜索，针对标准SMO的缺点，出现了以下几种改进方法，它们同样是通过KKT条件来选择乘子，不同之处为使用对偶问题的KKT条件。

1、通过Maximal Violating Pair选择优化乘子

原问题的对偶问题指的是：

$max \quad \quad W(\alpha)=\sum\limits_{i=1}^{n}\alpha-\frac{1}{2}\sum\limits_{i,j=1}^{n}{y_iy_j\alpha_i\alpha_j(K(x_i,x_j))$

$s.t.$ $\sum\limits_{i=1}^{n}y_i\alpha_i=0$

$0 \leq \alpha_i \leq C$ $(i=1,2,...n)$

它的拉格朗日方程可以写为：

$L(\alpha_i,\delta_i,\mu_i,\beta)=\frac{1}{2}\sum\limits_{i,j=1}^{n}{y_iy_j\alpha_i\alpha_j(K(x_i,x_j))-\sum\limits_{i=1}^{n}\alpha$

$-\sum\limits_{i=1}^{n}\alpha_i\delta_i+\sum\limits_{i=1}^{n}\mu_i(\alpha_i-C)+\beta\sum\limits_{i=1}^{n}\alpha_i y_i$

定义 $F_i=w^Tx_i -y_i=\sum\limits_{j=1}^{n}{y_j\alpha_jK(x_i,x_j)-y_i=y_i \nabla W(\alpha_i)$ ，则对偶问题的KKT条件为：

$\begin{cases} \(F_i+\beta)y_i-\delta_i+\mu_i =0\\ \ \delta_i \geq 0\\ \ \delta_i \alpha_i=0\\ \ \mu_i \geq 0\\ \mu_i(\alpha_i-C)=0 \end{cases}$

总结以下可分为3种情况：

$\begin{cases} \ \alpha_i=0 \Leftrightarrow (F_i+\beta)y_i \geq 0\\ \ 0<\alpha_i<C \Leftrightarrow (F_i+\beta)y_i = 0\\ \ \alpha_i=C \Leftrightarrow (F_i+\beta)y_i \leq 0 \end{cases}$

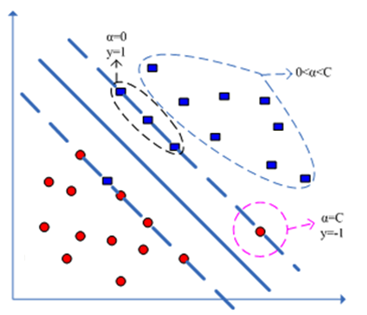
分类标记 $y_i$ 可以取1或-1，按照正类和负类区分指标集， $I_0=\{0<\alpha_i<C\}$ 、 $I_1=\{\alpha_i=0 && y_i=1\}$ 、 $I_2=\{\alpha_i=C&&y_i=-1\}$ 、 $I_3=\{\alpha_i=0&&y_i=-1\}$ 、 $I_4=\{\alpha_i=C&&y_i=1\}$ ，如图：

图一

整理一下就得到KKT条件的新形式：

$\begin{cases} \ \beta \geq -F_i \quad\quad\quad\quad i\in \{I_0 \bigcup I_1 \bigcup I_2\}\\ \ \beta \leq -F_i \quad\quad\quad\quad i\in \{I_0 \bigcup I_3 \bigcup I_4\}\\ \end{cases}$

从图上也可以看到，当分类器对全部样本都分类正确的时候，必有：

$F_i>F_j \quad\quad\quad\quad i\in {I_0\bigcup I_1 \bigcup I_2} \quad and \quad j\in {I_0\bigcup I_3 \bigcup I_4}$

像标准SMO一样，要精确达到最优值显然也是没必要的，因此这里也需要加个容忍值。

引入容忍值后的KKT条件为：

$\begin{cases} \ \alpha_i=0 \Leftrightarrow (F_i+\beta)y_i \geq -\iota\\ \ 0<\alpha_i<C \Leftrightarrow |F_i+\beta| \leq \iota\\ \ \alpha_i=C \Leftrightarrow (F_i+\beta)y_i \leq \iota \end{cases}$

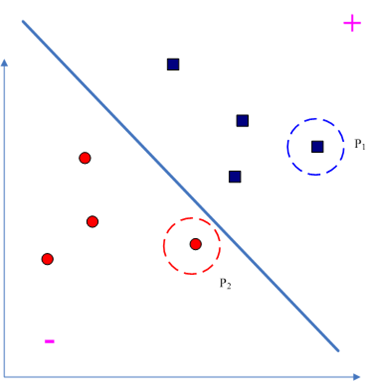
根据前面的说明可以定义“违反对” $pair(i,j)$ ：

$i\in \{I_0 \bigcup I_1 \bigcup I_2\}, j\in \{I_0 \bigcup I_3 \bigcup I_4\} \quad and\quad F_i<F_j-2\iota$

$i\in \{I_0 \bigcup I_3 \bigcup I_4\}, j\in \{I_0 \bigcup I_1 \bigcup I_2\} \quad and\quad F_i>F_j+2\iota$

那么我们到底要优化哪两个拉格朗日乘子呢？由“违反对”的定义可知， $F_i$ 和 $F_j$ 差距最大的那两个点最违反KKT条件的，描述为：

$\begin{cases} \ m(\alpha)=max\{-F_i:\quad\quad i\in I_0\bigcup I_1 \bigcup I_2\}\\ \ M(\alpha)=min\{-F_j:\quad\quad j\in I_0\bigcup I_3 \bigcup I_4\}\\ \ m(\alpha) > M(\alpha) + 2\iota \\ \end{cases}$

于是 $pair(i,j)$ 就是一个“Maximal Violating Pair，一个示意图如下，其中 $P_1$ 和 $P_2$ 就是一对MVP：

2、通过Second Order Information选择优化乘子

不论是通过一阶信息还是二阶信息来选择优化乘子，都是基于以下这个定理：

定理一：如果 $y_iy_jK_{i,j}$ 矩阵为半正定矩阵，当且仅当待优化乘子为“违反对”时，对于SMO类型的算法，其目标函数严格递减(如： $w(\alpha^{k+1}) < w(\alpha^{k})$ )。

First Order Information选择方法我就不介绍了，直接看Second Order Information选择方法：

当选定一个乘子后，另一个乘子选择的条件是使得当前“乘子对”为“违反对”且能使目标函数值最小，在最优化迭代类型方法中非常重要的一个工具就是函数的taylor展开式，优化的过程可以概括为一系列选搜索方向、选搜索步长的过程，对目标函数w展开得：

$W(\alpha^{k}+d) \approx W(\alpha^{k})+\nabla W(\alpha^{k})^Td+\frac{1}{2} d^T \nabla^{2} W(\alpha^{k})d$ ，这里d分别为两个待选择乘子的优化方向。

于是最小化 $W(\alpha^{k}+d)$ 就变成了：

$min \quad \quad \quad \quad \quad \quad \nabla W(\alpha^{k})^Td+\frac{1}{2} d^T \nabla^{2} W(\alpha^{k})d$

由优化条件可知：

$\begin{cases} \ y_1\alpha_1 + y_2\alpha_2 +\sum\limits_{i=3}^{n}y_i\alpha_i=0\\ \ y_1(\alpha_1+d_1) + y_2(\alpha_2 +d_2)+\sum\limits_{i=3}^{n}y_i\alpha_i =0\\ \end{cases}$

$\Rightarrow \sum\limits_{i=1}^{2}y_id_i=0$

$0 \leq \alpha_i \leq C$

$\Rightarrow \begin{cases} \ d_i \geq 0 \quad \quad \quad \quad if \alpha__i = 0\\ \ d_i \leq 0 \quad \quad \quad \quad if \alpha__i = C\\ \end{cases}$

这样选择乘子的过程就变成了以下优化问题：

$Sub(B) = min \quad \quad \quad \quad \quad \quad \nabla W(\alpha^{k})^Td+\frac{1}{2} d^T \nabla^{2} W(\alpha^{k})d$

$s.t.$ $\sum\limits_{i=1}^{2}y_id_i=0$

$d_i \geq 0 \quad \quad \quad \quad if \quad \quad \quad \quad \alpha__i = 0$

$d_i \leq 0 \quad \quad \quad \quad if \quad \quad \quad \quad \alpha__i = C$ $(i=1,2)$

总结通过Second Order Information选择优化乘子的方法如下：

1、首先选择一个乘子，条件如下：

$i \in argmax\{-F_i|\ \quad \quad \quad \quad i\in I_{up}\}$

2、选择另外一个乘子的过程就是求解 $Sub(B)$ 的过程，设 $j$ 为第二个乘子，则有：

$Sub(B)=[\nabla W(\alpha^k)_i,\nabla W(\alpha^k)_j] \left[ d_i\\ d_j \right]$

$+\frac{1}{2}[d_i,d_j] \left[ y_i y_i K_{i,i},\quad y_i y_j K_{i,j}\\ y_j y_i K_{j,i},\quad y_j y_j K_{j,j} \right] \left[ d_i\\ d_j \right]$

将条件：

$\sum\limits_{i=1}^{2}y_id_i=0$

带入有：

$Sub(B)=(K_{i,i}+K_{j,j}-2K_{i,j})d_j^2-\nabla W(\alpha^k)_iy_iy_jd_j +\nabla W(\alpha^k)_j d_j$

于是目标函数在 $-\frac{-\nabla W(\alpha^k)_iy_iy_j +\nabla W(\alpha^k)_j }{(K_{i,i}+K_{j,j}-2K_{i,j})}$ 处达到最小值：

$objvalue=-\frac{(-\nabla W(\alpha^k)_iy_iy_j +\nabla W(\alpha^k))_j ^2}{2(K_{i,i}+K_{j,j}-2K_{i,j})}$

用式子表示就是：

$j \in argmin\{objvalue|k \in I_{low},\quad \quad -F_k<-F_i\}$

当 $K_{i,i}+K_{j,j}-2K_{i,j}<=0$ 这种情况出现时可以用一个很小的值来代替它，具体可见《A study on SMO-type decomposition methods for support vector machines》一文中“Non-Positive Definite Kernel Matrices”小节。

4、算法实现

将代码加入到了LeftNotEasy的pymining项目中了，可以从http://code.google.com/p/python-data-mining-platform/下载。

几点说明：

1、训练和测试数据格式为：value1 value2 value3 …… valuen，label=+1，数据集放在***.data中，对应的label放在***.labels中，也可以使用libsvm的数据集；

2、分类器目前支持的核为RBF、Linear、Polynomial、Sigmoid、将来支持String Kernel；

3、训练集和测试集的输入支持dense matrix 和 sparse matrix，其中sparse matrix采用CSR表示法；

4、对于不平衡数据的处理一般来说从三个方面入手：

1)、对正例和负例赋予不同的C值，例如正例远少于负例，则正例的C值取得较大，这种方法的缺点是可能会偏离原始数据的概率分布；

2)、对训练集的数据进行预处理即对数量少的样本以某种策略进行采样，增加其数量或者减少数量多的样本，典型的方法如：随机插入法，缺点是可能出现

overfitting，较好的是：Synthetic Minority Over-sampling TEchnique(SMOTE)，其缺点是只能应用在具体的特征空间中，不适合处理那些无法用

特征向量表示的问题，当然增加样本也意味着训练时间可能增加；

3)、基于核函数的不平衡数据处理。

本文就以容易实现为原则，采用第一种方式，配置文件中的节点<c>中的值代表的是正例的代价值，模型中的npRatio用来计算负例的代价值，例如正例远多于负例，则这个比率就大于一，反之亦然，原理如下图所示：

$y_1$ 和 $y_2$ 异号且 $y_1 =-1$ 的情形( $y_1 =1$ 的情况类似)

$y_1$ 和 $y_2$ 同号的情形

5、算法最耗时的地方是优化乘子的选择和更新一阶导数信息，这两个地方都需要去计算核函数值，而核函数值的计算最终都需要去做内积运算，这就意味着原始空间的维度很高会增加内积运算的时间；对于dense matrix我就直接用numpy的dot了，而sparse matrix采用的是CSR表示法，求它的内积我实验过的方法有三种，第一种不需要额外空间，但时间复杂度为O(nlgn)，第二种需要一个hash表(用dictionary代替了)，时间复杂度为线性，第三种需要一个bitmap(使用BitVector)，时间复杂度也为线性，实际使用中第一种速度最快，我就暂时用它了，应该还有更快的方法，希望高人们能指点一下；另外由于使用dictionary缓存核矩阵，遇到训练数据很大的数据集很容易挂掉，所以在程序中，当dictionary的内存占用达到配置文件的阈值时会将其中相对次要的元素删掉，保留对角线上的内积值。

6、使用psyco

相对于c，python在进行高维度数值计算时表现的会比较差，为了加快数值计算的速度，我使用了psyco来进行加速，它的使用很简单，加两句话就行，用程序测试一下使用psyco之前和之后的表现：

定义一个1164维的向量，代码如下：

        1: import time

       2: import psyco

       3: psyco.full()

       4:  

       5: def dot():

       6:     vec =[0.0081484941037,0.088244064232,-0.0116517274912,0.0175709303652,-0.0626241393835,-0.0854107365903,-0.0351575090354,0.0380456765128,0.0180095979816,-0.0209914241928,0.163106660981,0.127053320056,-0.0335430235607,-0.0109767864904,0.0709995225815,0.0167076809919,0.027726097262,-0.0311204836595,-0.0259199476295,0.180810035412,-0.0075547491507,-0.0081006110325,0.0270585413405,-0.0148313935713,0.0337146203424,0.0736048267004,-0.182810465676,-0.0267899729122,0.000179219280158,-0.0981396318556,0.0162153149149,0.0158205889243,0.0135732439379,-0.0122793913668,-0.0248816557428,-0.0839578376417,0.00599848509353,0.114707262204,-0.0328007287819,0.0467560652885,0.313179556657,0.024121214556,-0.0553332419857,-0.00684296908044,0.174685776575,0.00418298437096,0.015624947957,-0.0357577181683,-0.0335658241296,-0.0413500938049,0.00890996222676,-0.191520167295,-0.02223857119,-0.00900410728578,-0.00101642281143,-0.0751063838566,-0.00779308778792,-0.0339048097301,-0.29873321989,-0.00751397119331,0.0020689071961,-0.0334433996129,0.0798526578962,-0.00314060942661,0.000994142874497,-0.00385208084616,0.00639638012896,0.00432347948574,-0.0295723516279,-0.0282409806726,-0.243877258982,0.0306503469536,-0.0229985748532,0.0284501391965,-0.198174324275,-0.0179711916393,0.0143267555469,-0.0287066071347,0.000282523969584,0.0616495560776,-0.0172220711262,-0.0687083629936,-0.00370051948645,-0.0219797414557,0.15847905705,0.0354483161821,0.0763267553204,-0.0429680349387,0.438909021868,-0.0549235929403,-0.00176280411289,0.0168842161271,-0.0245477451033,0.103534103547,0.190875334952,-0.0160077971357,-1.13916725717,-0.0578280272522,0.618283515386,0.0218745277242,-0.0637461100123,0.00666421528081,0.0276254007423,-0.042759151837,-0.0145850642315,-0.00880446485194,0.000126716038755,0.00433140420099,0.0308245755082,-0.00623921726713,-0.0318217746795,-0.0382440579868,0.000428347914493,0.000530399307534,-0.0759717737756,0.0354515033891,0.130639143673,-0.141494874567,0.0838856126349,-0.0194418010364,0.0137972983237,0.000531338760413,0.00134150184801,0.261957858812,0.0237711884021,0.0230326428759,0.0219937855594,0.00719528755352,0.0333485055281,0.00833840466389,-0.0250022671701,0.0732187999699,0.0409463350505,-0.00163879777058,0.0323944604152,0.0248038687327,0.00763331851835,-0.00540476791599,-0.0700331001035,0.636770876239,0.0270714128914,-0.0562305127792,0.0369742780132,-0.00482469423333,-0.153208622043,-0.169948249631,0.0822114655752,-0.000810202457017,0.0592939745916,0.0210041288368,0.0424686903816,0.013082261434,-0.0270151903807,0.0226204321573,0.00337807861336,0.0552972148331,0.00137329198924,0.00410977518032,-0.0788631223297,0.0195763268983,-0.011867418399,0.000136137516823,0.0489199529798,-0.0272194722771,0.0126117026801,-0.422521768213,0.0175167663074,-0.513577519799,-0.304908016713,-0.0153815043354,0.0143756230195,0.038892601783,0.00785100547614,0.024633644749,0.0565278241742,-0.019980734894,0.100938716186,0.0274989424604,0.0103429343526,-0.0533430239958,0.0319011843986,-0.0168859775771,-0.0443695710743,-0.0079129398118,-0.0125144644331,0.13605025411,-0.0162963376194,-0.000710295461299,0.0144422401202,-0.0184620116687,0.0804442274609,-0.0234468286624,-0.0238108738443,0.00860171509498,0.0081484941037,0.088244064232,-0.0116517274912,0.0175709303652,-0.0626241393835,-0.0854107365903,-0.0351575090354,0.0380456765128,0.0180095979816,-0.0209914241928,0.163106660981,0.127053320056,-0.0335430235607,-0.0109767864904,0.0709995225815,0.0167076809919,0.027726097262,-0.0311204836595,-0.0259199476295,0.180810035412,-0.0075547491507,-0.0081006110325,0.0270585413405,-0.0148313935713,0.0337146203424,0.0736048267004,-0.182810465676,-0.0267899729122,0.000179219280158,-0.0981396318556,0.0162153149149,0.0158205889243,0.0135732439379,-0.0122793913668,-0.0248816557428,-0.0839578376417,0.00599848509353,0.114707262204,-0.0328007287819,0.0467560652885,0.313179556657,0.024121214556,-0.0553332419857,-0.00684296908044,0.174685776575,0.00418298437096,0.015624947957,-0.0357577181683,-0.0335658241296,-0.0413500938049,0.00890996222676,-0.191520167295,-0.02223857119,-0.00900410728578,-0.00101642281143,-0.0751063838566,-0.00779308778792,-0.0339048097301,-0.29873321989,-0.00751397119331,0.0020689071961,-0.0334433996129,0.0798526578962,-0.00314060942661,0.000994142874497,-0.00385208084616,0.00639638012896,0.00432347948574,-0.0295723516279,-0.0282409806726,-0.243877258982,0.0306503469536,-0.0229985748532,0.0284501391965,-0.198174324275,-0.0179711916393,0.0143267555469,-0.0287066071347,0.000282523969584,0.0616495560776,-0.0172220711262,-0.0687083629936,-0.00370051948645,-0.0219797414557,0.15847905705,0.0354483161821,0.0763267553204,-0.0429680349387,0.438909021868,-0.0549235929403,-0.00176280411289,0.0168842161271,-0.0245477451033,0.103534103547,0.190875334952,-0.0160077971357,-1.13916725717,-0.0578280272522,0.618283515386,0.0218745277242,-0.0637461100123,0.00666421528081,0.0276254007423,-0.042759151837,-0.0145850642315,-0.00880446485194,0.000126716038755,0.00433140420099,0.0308245755082,-0.00623921726713,-0.0318217746795,-0.0382440579868,0.000428347914493,0.000530399307534,-0.0759717737756,0.0354515033891,0.130639143673,-0.141494874567,0.0838856126349,-0.0194418010364,0.0137972983237,0.000531338760413,0.00134150184801,0.261957858812,0.0237711884021,0.0230326428759,0.0219937855594,0.00719528755352,0.0333485055281,0.00833840466389,-0.0250022671701,0.0732187999699,0.0409463350505,-0.00163879777058,0.0323944604152,0.0248038687327,0.00763331851835,-0.00540476791599,-0.0700331001035,0.636770876239,0.0270714128914,-0.0562305127792,0.0369742780132,-0.00482469423333,-0.153208622043,-0.169948249631,0.0822114655752,-0.000810202457017,0.0592939745916,0.0210041288368,0.0424686903816,0.013082261434,-0.0270151903807,0.0226204321573,0.00337807861336,0.0552972148331,0.00137329198924,0.00410977518032,-0.0788631223297,0.0195763268983,-0.011867418399,0.000136137516823,0.0489199529798,-0.0272194722771,0.0126117026801,-0.422521768213,0.0175167663074,-0.513577519799,-0.304908016713,-0.0153815043354,0.0143756230195,0.038892601783,0.00785100547614,0.024633644749,0.0565278241742,-0.019980734894,0.100938716186,0.0274989424604,0.0103429343526,-0.0533430239958,0.0319011843986,-0.0168859775771,-0.0443695710743,-0.0079129398118,-0.0125144644331,0.13605025411,-0.0162963376194,-0.000710295461299,0.0144422401202,-0.0184620116687,0.0804442274609,-0.0234468286624,-0.0238108738443,0.00860171509498,0.0081484941037,0.088244064232,-0.0116517274912,0.0175709303652,-0.0626241393835,-0.0854107365903,-0.0351575090354,0.0380456765128,0.0180095979816,-0.0209914241928,0.163106660981,0.127053320056,-0.0335430235607,-0.0109767864904,0.0709995225815,0.0167076809919,0.027726097262,-0.0311204836595,-0.0259199476295,0.180810035412,-0.0075547491507,-0.0081006110325,0.0270585413405,-0.0148313935713,0.0337146203424,0.0736048267004,-0.182810465676,-0.0267899729122,0.000179219280158,-0.0981396318556,0.0162153149149,0.0158205889243,0.0135732439379,-0.0122793913668,-0.0248816557428,-0.0839578376417,0.00599848509353,0.114707262204,-0.0328007287819,0.0467560652885,0.313179556657,0.024121214556,-0.0553332419857,-0.00684296908044,0.174685776575,0.00418298437096,0.015624947957,-0.0357577181683,-0.0335658241296,-0.0413500938049,0.00890996222676,-0.191520167295,-0.02223857119,-0.00900410728578,-0.00101642281143,-0.0751063838566,-0.00779308778792,-0.0339048097301,-0.29873321989,-0.00751397119331,0.0020689071961,-0.0334433996129,0.0798526578962,-0.00314060942661,0.000994142874497,-0.00385208084616,0.00639638012896,0.00432347948574,-0.0295723516279,-0.0282409806726,-0.243877258982,0.0306503469536,-0.0229985748532,0.0284501391965,-0.198174324275,-0.0179711916393,0.0143267555469,-0.0287066071347,0.000282523969584,0.0616495560776,-0.0172220711262,-0.0687083629936,-0.00370051948645,-0.0219797414557,0.15847905705,0.0354483161821,0.0763267553204,-0.0429680349387,0.438909021868,-0.0549235929403,-0.00176280411289,0.0168842161271,-0.0245477451033,0.103534103547,0.190875334952,-0.0160077971357,-1.13916725717,-0.0578280272522,0.618283515386,0.0218745277242,-0.0637461100123,0.00666421528081,0.0276254007423,-0.042759151837,-0.0145850642315,-0.00880446485194,0.000126716038755,0.00433140420099,0.0308245755082,-0.00623921726713,-0.0318217746795,-0.0382440579868,0.000428347914493,0.000530399307534,-0.0759717737756,0.0354515033891,0.130639143673,-0.141494874567,0.0838856126349,-0.0194418010364,0.0137972983237,0.000531338760413,0.00134150184801,0.261957858812,0.0237711884021,0.0230326428759,0.0219937855594,0.00719528755352,0.0333485055281,0.00833840466389,-0.0250022671701,0.0732187999699,0.0409463350505,-0.00163879777058,0.0323944604152,0.0248038687327,0.00763331851835,-0.00540476791599,-0.0700331001035,0.636770876239,0.0270714128914,-0.0562305127792,0.0369742780132,-0.00482469423333,-0.153208622043,-0.169948249631,0.0822114655752,-0.000810202457017,0.0592939745916,0.0210041288368,0.0424686903816,0.013082261434,-0.0270151903807,0.0226204321573,0.00337807861336,0.0552972148331,0.00137329198924,0.00410977518032,-0.0788631223297,0.0195763268983,-0.011867418399,0.000136137516823,0.0489199529798,-0.0272194722771,0.0126117026801,-0.422521768213,0.0175167663074,-0.513577519799,-0.304908016713,-0.0153815043354,0.0143756230195,0.038892601783,0.00785100547614,0.024633644749,0.0565278241742,-0.019980734894,0.100938716186,0.0274989424604,0.0103429343526,-0.0533430239958,0.0319011843986,-0.0168859775771,-0.0443695710743,-0.0079129398118,-0.0125144644331,0.13605025411,-0.0162963376194,-0.000710295461299,0.0144422401202,-0.0184620116687,0.0804442274609,-0.0234468286624,-0.0238108738443,0.00860171509498,0.0081484941037,0.088244064232,-0.0116517274912,0.0175709303652,-0.0626241393835,-0.0854107365903,-0.0351575090354,0.0380456765128,0.0180095979816,-0.0209914241928,0.163106660981,0.127053320056,-0.0335430235607,-0.0109767864904,0.0709995225815,0.0167076809919,0.027726097262,-0.0311204836595,-0.0259199476295,0.180810035412,-0.0075547491507,-0.0081006110325,0.0270585413405,-0.0148313935713,0.0337146203424,0.0736048267004,-0.182810465676,-0.0267899729122,0.000179219280158,-0.0981396318556,0.0162153149149,0.0158205889243,0.0135732439379,-0.0122793913668,-0.0248816557428,-0.0839578376417,0.00599848509353,0.114707262204,-0.0328007287819,0.0467560652885,0.313179556657,0.024121214556,-0.0553332419857,-0.00684296908044,0.174685776575,0.00418298437096,0.015624947957,-0.0357577181683,-0.0335658241296,-0.0413500938049,0.00890996222676,-0.191520167295,-0.02223857119,-0.00900410728578,-0.00101642281143,-0.0751063838566,-0.00779308778792,-0.0339048097301,-0.29873321989,-0.00751397119331,0.0020689071961,-0.0334433996129,0.0798526578962,-0.00314060942661,0.000994142874497,-0.00385208084616,0.00639638012896,0.00432347948574,-0.0295723516279,-0.0282409806726,-0.243877258982,0.0306503469536,-0.0229985748532,0.0284501391965,-0.198174324275,-0.0179711916393,0.0143267555469,-0.0287066071347,0.000282523969584,0.0616495560776,-0.0172220711262,-0.0687083629936,-0.00370051948645,-0.0219797414557,0.15847905705,0.0354483161821,0.0763267553204,-0.0429680349387,0.438909021868,-0.0549235929403,-0.00176280411289,0.0168842161271,-0.0245477451033,0.103534103547,0.190875334952,-0.0160077971357,-1.13916725717,-0.0578280272522,0.618283515386,0.0218745277242,-0.0637461100123,0.00666421528081,0.0276254007423,-0.042759151837,-0.0145850642315,-0.00880446485194,0.000126716038755,0.00433140420099,0.0308245755082,-0.00623921726713,-0.0318217746795,-0.0382440579868,0.000428347914493,0.000530399307534,-0.0759717737756,0.0354515033891,0.130639143673,-0.141494874567,0.0838856126349,-0.0194418010364,0.0137972983237,0.000531338760413,0.00134150184801,0.261957858812,0.0237711884021,0.0230326428759,0.0219937855594,0.00719528755352,0.0333485055281,0.00833840466389,-0.0250022671701,0.0732187999699,0.0409463350505,-0.00163879777058,0.0323944604152,0.0248038687327,0.00763331851835,-0.00540476791599,-0.0700331001035,0.636770876239,0.0270714128914,-0.0562305127792,0.0369742780132,-0.00482469423333,-0.153208622043,-0.169948249631,0.0822114655752,-0.000810202457017,0.0592939745916,0.0210041288368,0.0424686903816,0.013082261434,-0.0270151903807,0.0226204321573,0.00337807861336,0.0552972148331,0.00137329198924,0.00410977518032,-0.0788631223297,0.0195763268983,-0.011867418399,0.000136137516823,0.0489199529798,-0.0272194722771,0.0126117026801,-0.422521768213,0.0175167663074,-0.513577519799,-0.304908016713,-0.0153815043354,0.0143756230195,0.038892601783,0.00785100547614,0.024633644749,0.0565278241742,-0.019980734894,0.100938716186,0.0274989424604,0.0103429343526,-0.0533430239958,0.0319011843986,-0.0168859775771,-0.0443695710743,-0.0079129398118,-0.0125144644331,0.13605025411,-0.0162963376194,-0.000710295461299,0.0144422401202,-0.0184620116687,0.0804442274609,-0.0234468286624,-0.0238108738443,0.00860171509498,0.0081484941037,0.088244064232,-0.0116517274912,0.0175709303652,-0.0626241393835,-0.0854107365903,-0.0351575090354,0.0380456765128,0.0180095979816,-0.0209914241928,0.163106660981,0.127053320056,-0.0335430235607,-0.0109767864904,0.0709995225815,0.0167076809919,0.027726097262,-0.0311204836595,-0.0259199476295,0.180810035412,-0.0075547491507,-0.0081006110325,0.0270585413405,-0.0148313935713,0.0337146203424,0.0736048267004,-0.182810465676,-0.0267899729122,0.000179219280158,-0.0981396318556,0.0162153149149,0.0158205889243,0.0135732439379,-0.0122793913668,-0.0248816557428,-0.0839578376417,0.00599848509353,0.114707262204,-0.0328007287819,0.0467560652885,0.313179556657,0.024121214556,-0.0553332419857,-0.00684296908044,0.174685776575,0.00418298437096,0.015624947957,-0.0357577181683,-0.0335658241296,-0.0413500938049,0.00890996222676,-0.191520167295,-0.02223857119,-0.00900410728578,-0.00101642281143,-0.0751063838566,-0.00779308778792,-0.0339048097301,-0.29873321989,-0.00751397119331,0.0020689071961,-0.0334433996129,0.0798526578962,-0.00314060942661,0.000994142874497,-0.00385208084616,0.00639638012896,0.00432347948574,-0.0295723516279,-0.0282409806726,-0.243877258982,0.0306503469536,-0.0229985748532,0.0284501391965,-0.198174324275,-0.0179711916393,0.0143267555469,-0.0287066071347,0.000282523969584,0.0616495560776,-0.0172220711262,-0.0687083629936,-0.00370051948645,-0.0219797414557,0.15847905705,0.0354483161821,0.0763267553204,-0.0429680349387,0.438909021868,-0.0549235929403,-0.00176280411289,0.0168842161271,-0.0245477451033,0.103534103547,0.190875334952,-0.0160077971357,-1.13916725717,-0.0578280272522,0.618283515386,0.0218745277242,-0.0637461100123,0.00666421528081,0.0276254007423,-0.042759151837,-0.0145850642315,-0.00880446485194,0.000126716038755,0.00433140420099,0.0308245755082,-0.00623921726713,-0.0318217746795,-0.0382440579868,0.000428347914493,0.000530399307534,-0.0759717737756,0.0354515033891,0.130639143673,-0.141494874567,0.0838856126349,-0.0194418010364,0.0137972983237,0.000531338760413,0.00134150184801,0.261957858812,0.0237711884021,0.0230326428759,0.0219937855594,0.00719528755352,0.0333485055281,0.00833840466389,-0.0250022671701,0.0732187999699,0.0409463350505,-0.00163879777058,0.0323944604152,0.0248038687327,0.00763331851835,-0.00540476791599,-0.0700331001035,0.636770876239,0.0270714128914,-0.0562305127792,0.0369742780132,-0.00482469423333,-0.153208622043,-0.169948249631,0.0822114655752,-0.000810202457017,0.0592939745916,0.0210041288368,0.0424686903816,0.013082261434,-0.0270151903807,0.0226204321573,0.00337807861336,0.0552972148331,0.00137329198924,0.00410977518032,-0.0788631223297,0.0195763268983,-0.011867418399,0.000136137516823,0.0489199529798,-0.0272194722771,0.0126117026801,-0.422521768213,0.0175167663074,-0.513577519799,-0.304908016713,-0.0153815043354,0.0143756230195,0.038892601783,0.00785100547614,0.024633644749,0.0565278241742,-0.019980734894,0.100938716186,0.0274989424604,0.0103429343526,-0.0533430239958,0.0319011843986,-0.0168859775771,-0.0443695710743,-0.0079129398118,-0.0125144644331,0.13605025411,-0.0162963376194,-0.000710295461299,0.0144422401202,-0.0184620116687,0.0804442274609,-0.0234468286624,-0.0238108738443,0.00860171509498,0.0081484941037,0.088244064232,-0.0116517274912,0.0175709303652,-0.0626241393835,-0.0854107365903,-0.0351575090354,0.0380456765128,0.0180095979816,-0.0209914241928,0.163106660981,0.127053320056,-0.0335430235607,-0.0109767864904,0.0709995225815,0.0167076809919,0.027726097262,-0.0311204836595,-0.0259199476295,0.180810035412,-0.0075547491507,-0.0081006110325,0.0270585413405,-0.0148313935713,0.0337146203424,0.0736048267004,-0.182810465676,-0.0267899729122,0.000179219280158,-0.0981396318556,0.0162153149149,0.0158205889243,0.0135732439379,-0.0122793913668,-0.0248816557428,-0.0839578376417,0.00599848509353,0.114707262204,-0.0328007287819,0.0467560652885,0.313179556657,0.024121214556,-0.0553332419857,-0.00684296908044,0.174685776575,0.00418298437096,0.015624947957,-0.0357577181683,-0.0335658241296,-0.0413500938049,0.00890996222676,-0.191520167295,-0.02223857119,-0.00900410728578,-0.00101642281143,-0.0751063838566,-0.00779308778792,-0.0339048097301,-0.29873321989,-0.00751397119331,0.0020689071961,-0.0334433996129,0.0798526578962,-0.00314060942661,0.000994142874497,-0.00385208084616,0.00639638012896,0.00432347948574,-0.0295723516279,-0.0282409806726,-0.243877258982,0.0306503469536,-0.0229985748532,0.0284501391965,-0.198174324275,-0.0179711916393,0.0143267555469,-0.0287066071347,0.000282523969584,0.0616495560776,-0.0172220711262,-0.0687083629936,-0.00370051948645,-0.0219797414557,0.15847905705,0.0354483161821,0.0763267553204,-0.0429680349387,0.438909021868,-0.0549235929403,-0.00176280411289,0.0168842161271,-0.0245477451033,0.103534103547,0.190875334952,-0.0160077971357,-1.13916725717,-0.0578280272522,0.618283515386,0.0218745277242,-0.0637461100123,0.00666421528081,0.0276254007423,-0.042759151837,-0.0145850642315,-0.00880446485194,0.000126716038755,0.00433140420099,0.0308245755082,-0.00623921726713,-0.0318217746795,-0.0382440579868,0.000428347914493,0.000530399307534,-0.0759717737756,0.0354515033891,0.130639143673,-0.141494874567,0.0838856126349,-0.0194418010364,0.0137972983237,0.000531338760413,0.00134150184801,0.261957858812,0.0237711884021,0.0230326428759,0.0219937855594,0.00719528755352,0.0333485055281,0.00833840466389,-0.0250022671701,0.0732187999699,0.0409463350505,-0.00163879777058,0.0323944604152,0.0248038687327,0.00763331851835,-0.00540476791599,-0.0700331001035,0.636770876239,0.0270714128914,-0.0562305127792,0.0369742780132,-0.00482469423333,-0.153208622043,-0.169948249631,0.0822114655752,-0.000810202457017,0.0592939745916,0.0210041288368,0.0424686903816,0.013082261434,-0.0270151903807,0.0226204321573,0.00337807861336,0.0552972148331,0.00137329198924,0.00410977518032,-0.0788631223297,0.0195763268983,-0.011867418399,0.000136137516823,0.0489199529798,-0.0272194722771,0.0126117026801,-0.422521768213,0.0175167663074,-0.513577519799,-0.304908016713,-0.0153815043354,0.0143756230195,0.038892601783,0.00785100547614,0.024633644749,0.0565278241742,-0.019980734894,0.100938716186,0.0274989424604,0.0103429343526,-0.0533430239958,0.0319011843986,-0.0168859775771,-0.0443695710743,-0.0079129398118,-0.0125144644331,0.13605025411,-0.0162963376194,-0.000710295461299,0.0144422401202,-0.0184620116687,0.0804442274609,-0.0234468286624,-0.0238108738443,0.00860171509498]

       7:     sum = 0.0

       8:     for i in range(len(vec)):

       9:         sum += vec[i] * vec[i]

      10:     return sum

      11:  

      12: if __name__ == "__main__": 

      13:     start = time.clock()

      14:     

      15:     for i in range(100000):

      16:         dot()

      17:  

      18:     print '\n dot product = ',dot(),'\n'

      19:  

      20:     end = time.clock()

      21:     print end - start, 'seconds.'

注释掉psyco.full()这句话后执行时间为：26.48s，去掉注释后执行时间为：4.6s，改成C代码执行时间为：0.58s，一般情况下psyco都会加快运行速度，当然和C相比其实还是差距明显的，相关链接如下：

1)、可爱的 Python: 用 Psyco 让 Python 运行得像 C 一样快》：http://www.ibm.com/developerworks/cn/linux/sdk/python/charm-28/

2)、psyco主页：http://psyco.sourceforge.net/download.html，在ubuntu下可以这么安装：sudo apt-get install python-psyco

7、关于分类器的评价采用如下指标：

1)、 $Recall = TP/(TP + FN)$

2)、 $Precision = TP/(TP + FP)$

3)、 $Accuracy = (TP + TN)/(TP + TN + FP + FN)$

4)、 $F\beta_1 = 2 * (Recall * Precision)/(1 + Precision + Recall)$

5)、 $F\beta_2 = 5 * (Recall * Precision)/(4 + Precision + Recall)$

6)、 $AUCb = (Recall + TN/(FP + TN))/2$

7)、 $ROC$ 、 $AUC$

8、运行环境：

OS：32bits ubuntu 10.04

CPU：Intel(R) Pentium(R) Dual CPU E2200 @ 2.20GHz

memory：DIMM DDR2 Synchronous 667 MHz (1.5 ns) 2G

IDE：Eclipse + Pydev

9、程序中用到的数据集主要来自UCI Data Set和Libsvm Data：

1)、pymining data：data/train.txt和data/test.txt

                     DATA     ------- 0 ex. ------- 1 ex. -------- 2 ex. ---------- 3 ex. ------------ Total
                 Training set       149 --------- 36   --------- 102 ---------- 63      ------------ 350
                 Validation set     85 --------- 14   --------- 35    ---------- 16      ------------ 150

Number of features：卡方检验过滤后

Total：1862

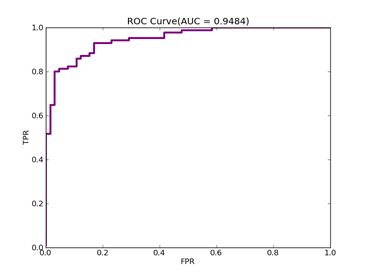
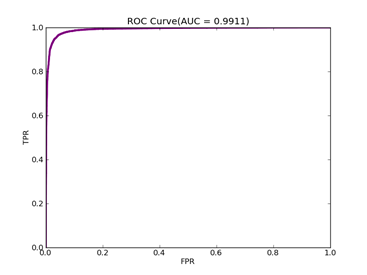
C = 100,kernel = RBF,gamma = 0.03,npRatio=1,测试结果如下：

                 (1)、类别0标记为1，其它标记为-1，
                 Recall = 0.929411764706 Precision = 0.840425531915 Accuracy = 0.86
                 F(beta=1) = 0.564005241516 F(beta=2) = 0.676883364786 AUCb = 0.849321266968

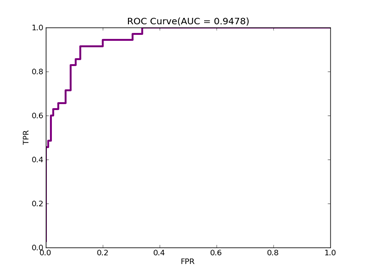
                 (2)、类别1标记为1，其它标记为-1，
                 Recall = 0.929411764706 Precision = 0.840425531915 Accuracy = 0.86
                 F(beta=1) = 0.564005241516 F(beta=2) = 0.676883364786 AUCb = 0.849321266968

                 (3)、类别2标记为1，其它标记为-1，
                 Recall = 0.6 Precision = 0.913043478261 Accuracy = 0.893333333333
                 F(beta=1) = 0.43598615917 F(beta=2) = 0.496845425868 AUCb = 0.791304347826

                 (4)、类别3标记为1，其它标记为-1，
                 Recall = 0.25 Precision = 1.0 Accuracy = 0.92
                 F(beta=1) = 0.222222222222 F(beta=2) = 0.238095238095 AUCb = 0.625

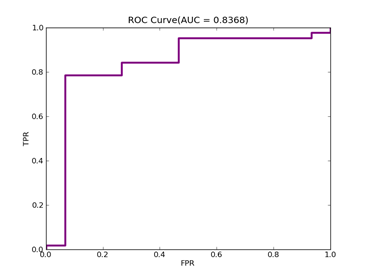
2)、Arcene：http://archive.ics.uci.edu/ml/datasets/Arcene

                 ARCENE -- Positive ex. -- Negative ex. – Total
                 Training set     44 ----------- 56 --------- 100
                 Validation set   44 ----------- 56 --------- 100

                 Number of variables/features/attributes：
                 Real: 7000
                 Probes: 3000
                 Total: 10000

                 C = 100,kernel = RBF,gamma = 0.000000001,npRatio=1,测试结果如下：
                 Recall = 0.772727272727 Precision = 0.85 Accuracy = 0.84
                 F(beta=1) = 0.500866551127 F(beta=2) = 0.584074373484 AUCb = 0.832792207792

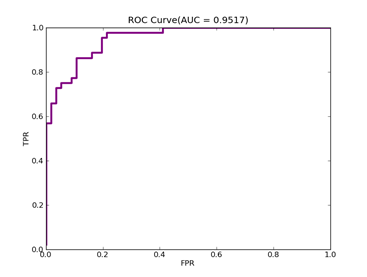
3)、SPECT Heart Data Set ：http://archive.ics.uci.edu/ml/datasets/SPECT+Heart

                 SPECT ------ Positive ex. -- Negative ex. – Total
                 Training set     40------------ 40---------- 80
                 Validation set   172 ---------- 15--------- 187

                 Attribute Information:
                 OVERALL_DIAGNOSIS: 0,1 (class attribute, binary)
                 F1: 0,1 (the partial diagnosis 1, binary)
                 F2: 0,1 (the partial diagnosis 2, binary)
                 F3: 0,1 (the partial diagnosis 3, binary)
                 F4: 0,1 (the partial diagnosis 4, binary)
                 F5: 0,1 (the partial diagnosis 5, binary)
                 F6: 0,1 (the partial diagnosis 6, binary)
                 F7: 0,1 (the partial diagnosis 7, binary)
                 F8: 0,1 (the partial diagnosis 8, binary)
                 F9: 0,1 (the partial diagnosis 9, binary)
                 F10: 0,1 (the partial diagnosis 10, binary)
                 F11: 0,1 (the partial diagnosis 11, binary)
                 F12: 0,1 (the partial diagnosis 12, binary)
                 F13: 0,1 (the partial diagnosis 13, binary)
                 F14: 0,1 (the partial diagnosis 14, binary)
                 F15: 0,1 (the partial diagnosis 15, binary)
                 F16: 0,1 (the partial diagnosis 16, binary)
                 F17: 0,1 (the partial diagnosis 17, binary)
                 F18: 0,1 (the partial diagnosis 18, binary)
                 F19: 0,1 (the partial diagnosis 19, binary)
                 F20: 0,1 (the partial diagnosis 20, binary)
                 F21: 0,1 (the partial diagnosis 21, binary)
                 F22: 0,1 (the partial diagnosis 22, binary)

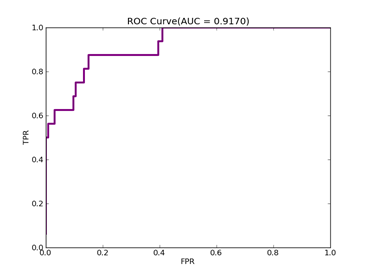
                 C = 100,kernel = RBF,gamma = 15,npRatio=1,测试结果如下：
                 Recall = 0.93023255814 Precision = 0.958083832335 Accuracy = 0.898395721925
                 F(beta=1) = 0.617135142954 F(beta=2) = 0.756787437329 AUCb = 0.731782945736

4)、Dexter：http://archive.ics.uci.edu/ml/datasets/Dexter

                 DEXTER -- Positive ex. -- Negative ex. – Total
                 Training set    150 ---------- 150 -------- 300
                 Validation set 150 ---------- 150 -------- 300
                 Test set         1000 --------- 1000 ------- 2000 (缺少label)

                 Number of variables/features/attributes:
                 Real: 9947
                 Probes: 10053
                 Total: 20000

                 C = 100,kernel = RBF, gamma = 0.000001,npRatio=1,测试结果如下：
                 Recall = 0.986666666667 Precision = 0.822222222222 Accuracy = 0.886666666667
                 F(beta=1) = 0.577637130802 F(beta=2) = 0.698291252232 AUCb = 0.886666666667

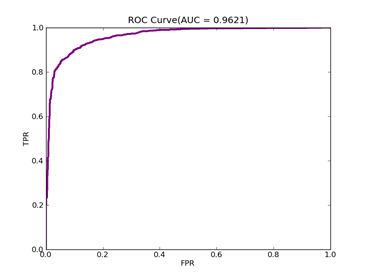
5)、Mushrooms：原始数据集在：http://archive.ics.uci.edu/ml/datasets/Mushroom

预处理以后的在：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary/mushrooms

MUSHROOMS-- Positive ex.（lbael=1） -- Negative ex.（lbael=2） – Total
Data set 3916 ----------------------- 4208 ------------------- 8124

Number of variables/features/attributes: 112

                 C = 100,kernel = RBF,gamma = 0.00001,npRatio=1,测试结果如下：
                 Recall = 1.0 Precision = 0.942615239887 Accuracy = 0.960897435897
                 F(beta=1) = 0.640664961637 F(beta=2) = 0.793097989552 AUCb = 0.945340501792

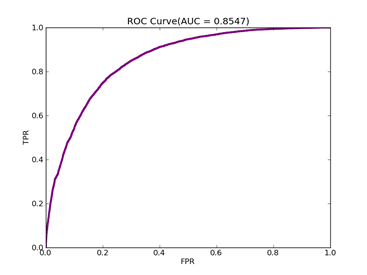
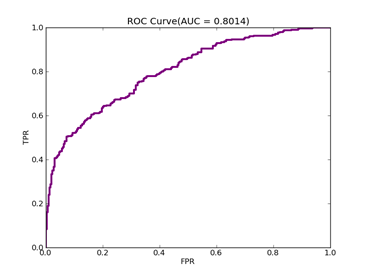
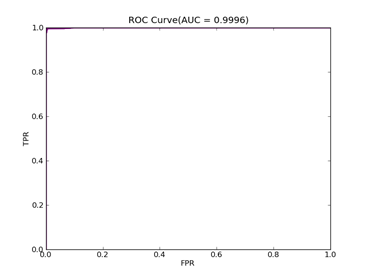6)、 Adult：原始数据集在：http://archive.ics.uci.edu/ml/datasets/Adult

预处理以后的在：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html a1a

ADULT ------ Positive ex.（lbael=+1） --- Negative ex.（lbael=-1） – Total
Training set 395 -------------------- 1210 ----------------- 1605

Validation set 7446 -------------------- 23510 ----------------- 30956

Number of variables/features/attributes: 123

                 C = 100,kernel = RBF,gamma = 0.08,npRatio=1,测试结果如下：
                 Recall = 0.598710717164 Precision = 0.588281868567 Accuracy = 0.802687685748
                 F(beta=1) = 0.322095887953 F(beta=2) = 0.339513363093 AUCb = 0.733000615919

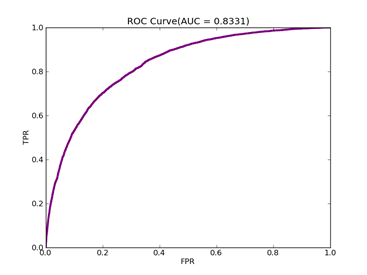由于正例少于负例,调整模型的npRatio=10,测试结果如下：

Recall = 0.620198764437 Precision = 0.602243088159 Accuracy = 0.810117586251
F(beta=1) = 0.336126156669 F(beta=2) = 0.357601319181 AUCb = 0.745233367757

其它参数不变，npRatio=100,测试结果如下：

Recall = 0.6952726296 Precision = 0.595399654974 Accuracy = 0.813057242538
F(beta=1) = 0.361435449815 F(beta=2) = 0.39122162696 AUCb = 0.772817088939

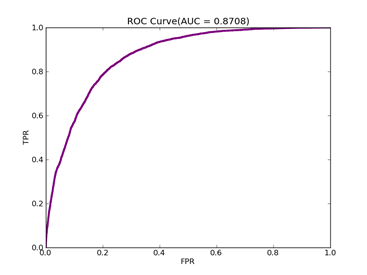可以从上面的实验看到处理不平衡数据时候，对正例和负例赋予不同的C值方法的作用。

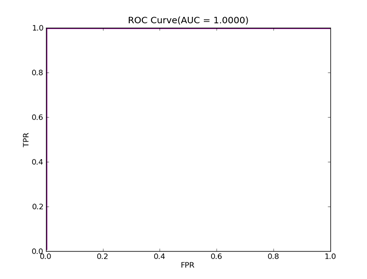
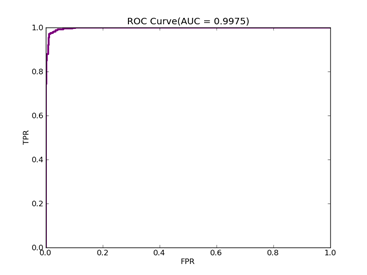
7）、Fourclass：数据集在：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary/fourclass

FOURCLASS-- Positive ex.（lbael=1） -- Negative ex.（lbael=2） – Total
Fourclass set 307 ----------------------- 557 ------------------- 864

Number of variables/features/attributes: 2

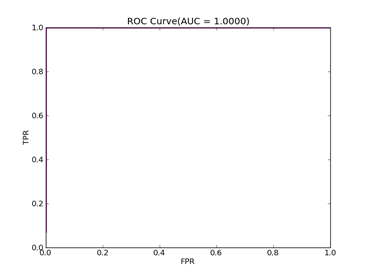
                 C = 100,kernel = RBF,gamma = 0.01,npRatio=1,测试结果如下：
                 Recall = 0.991071428571 Precision = 1.0 Accuracy = 0.996415770609
                 F(beta=1) = 0.662686567164 F(beta=2) = 0.827123695976 AUCb = 0.995535714286

8）、Splice：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html splice

SPLICE-- Positive ex.（lbael=1） -- Negative ex.（lbael=2） – Total
Training set 517 --------------------- 483 --------------- 1000

Validation set 1131 -------------------- 1044 -------------- 2175

Number of variables/features/attributes: 60

                 C = 100,kernel = RBF,gamma = 0.01,npRatio=1,测试结果如下：
                 Recall = 0.885057471264 Precision = 0.912488605287 Accuracy = 0.896091954023
                 F(beta=1) = 0.577366617352 F(beta=2) = 0.696505768897 AUCb = 0.896551724138

9)、RCV1.BINARY：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html

                 RCV1.BINARY------Total
                 Training set           20242
                 Validation set         677399

Number of features:
Total: 47236

C = 100,kernel = RBF,gamma = 0.01,npRatio=1,eps = 0.01测试结果如下：

Recall = 0.956610366919 Precision = 0.964097045588 Accuracy = 0.9593
F(beta=1) = 0.631535514017 F(beta=2) = 0.778847158177 AUCb = 0.959383756361

10)、Madelon：http://archive.ics.uci.edu/ml/datasets/Madelon

                 MADELON -- Positive ex. -- Negative ex. – Total
                 Training set     1000 --------- 1000 ------- 2000
                 Validation set   300 ---------- 300 -------- 600
                 Test set          900 ---------- 900 -------- 1800

                 Number of variables/features/attributes:
                 Real: 20
                 Probes: 480
                 Total: 500

C = 100,kernel = RBF,gamma = 0.000005,npRatio=1,eps = 0.001测试结果如下：

Recall = 0.673333333333 Precision = 0.724014336918 Accuracy = 0.708333333333
F(beta=1) = 0.406701950583 F(beta=2) = 0.451613474471 AUCb = 0.708333333333

11)、GISETTE：http://archive.ics.uci.edu/ml/datasets/Gisette

                 GISETTE -- Positive ex. -- Negative ex. – Total
                 Training set    3000 -------- 3000 ------- 6000
                 Validation set 500 --------- 500 ---------1000
                 Test set         3250 -------- 3250 ------- 6500

                 Number of variables/features/attributes:
                 Real: 2500
                 Probes: 2500
                 Total: 5000

C = 100,kernel = RBF,gamma = 0.00000000005,npRatio=1,eps = 0.001测试结果如下：

Recall = 0.972 Precision = 0.983805668016 Accuracy = 0.978
F(beta=1) = 0.647037875094 F(beta=2) = 0.802795761493 AUCb = 0.978

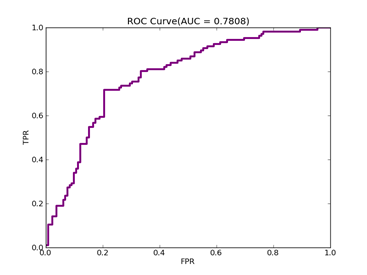
12)、Australian：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html

                 GISETTE -- Positive ex. -- Negative ex. – Total
                 Training set     201 --------- 251 -------- 452
                 Validation set 106 --------- 132 ---------238

Number of features:
Total: 14

C = 100,kernel = RBF,gamma = 0.0001,npRatio=150,eps = 0.001测试结果如下：

Recall = 0.801886792453 Precision = 0.643939393939 Accuracy = 0.714285714286
F(beta=1) = 0.422243001578 F(beta=2) = 0.474093808236 AUCb = 0.722913093196

13)、Svmguide1：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html

                 GISETTE -- Positive ex. -- Negative ex. – Total
                 Training set     2000 --------- 1089 -------- 3089
                 Validation set 2000 --------- 2000 ---------4000

Number of features:
Total: 4

C = 100,kernel = RBF,gamma = 0.01,npRatio=1,eps = 0.001测试结果如下：

Recall = 0.964 Precision = 0.957774465971 Accuracy = 0.96075
F(beta=1) = 0.632009483243 F(beta=2) = 0.7795759451 AUCb = 0.96075

5、并行点

如果期望在并行计算框架中运行SMO，我可以想到的并行点如下：

1)、选择最大违反对时，可以先在每台机器上找到局部MVP，最后由master选择全局MVP；

2)、更新一阶导数数组，各个机器更新自己本地部分就可以了；

3)、对sparse matrix向量求内积，可以用map函数映射为key/value对，其中key为column标号，value为对应的取值，reduce函数根据key计算乘积并累加。

想要使两个拉格朗日乘子的优化过程实现并行似乎很有难度，目前没有想到好方法。

6、总结

本文介绍了如何通过优化拉格朗日乘子的选择来提高SMO算法性能的方法，SMO算法的核心思想是每次选择两个拉格朗日乘子进行优化，因此其主要矛盾就落在了优先优化哪些乘子身上，目前对乘子选择最好的方法之一是利用对偶问题的KKT条件来寻找最大违反对(MVP)，而寻找MVP的方法又可以利用一阶信息和二阶信息，其中又以后者效果较好，它对MVP的选定不仅考虑它们之间 $F$ 值的差距，而且考虑两个乘子之间的伪距离 $K_{i,i}+K_{j,j}-2K_{i,j}$ 。

如果数据分布不平衡，训练出的分类器精度等常规指标可能很高，但是实际应用时就会出现问题，典型的例子是漏油检测，处理这类问题可以从三个方面入手：预处理数据集本身、使用不同惩罚系数、使用特殊核函数，它们各有优缺点，没有最好只有最合适，本文采用第二种方法，实现起来也比较容易，评价指标采用ROC Curve、AUC，本文绘制ROC的方法采用Libsvm中的方法。

参数选择直接影响到分类器的性能，涉及的主要参数有：惩罚系数C，这个值越大代表越不想放弃离群点；npRatio，如果数据分布很不平衡，可以用它来调节惩罚系数，负例远大于正例时，npRatio>1，负例的C值要小于正例的C值，反之亦然；核函数参数，依据具体核函数确定。本文没有给出选择最优参数的方法。

7、参考文献

1)、《Improvements to Platt’s SMO Algorithm for SVM Classifier Design》

2)、《A Study on SMO-type Decomposition Methods for Support Vector Machines》

3)、《The Analysis of Decomposition Methods for Support Vector Machines》

4)、《Working Set Selection Using Second Order Information for Training Support Vector Machines》

5)、《Making Large-Scale SVM Learning Practical》

6)、《Optimizing Area Under Roc Curve with SVMs》

7)、《Applying Support Vector Machines to Imbalanced Datasets》

8)、《SVMs Modeling for Highly Imbalanced》

posted on 2011-08-25 09:35 Leo Zhang 阅读(7122) 评论(15) 编辑收藏举报

刷新页面返回顶部

Leo Zhang