SVM学习——Sequential Minimal Optimization

1、前言

接触SVM也有一段时间了，从理论到实践都有了粗浅的认识，我认为SVM的发展可以划分为几个相对独立的部分，首先是SVM理论本身，包括寻找最大间隔分类超平面、引入核方法极大提高对非线性问题的处理能力、引入松弛变量的软间隔优化，用间隔定量的描述置信风险等等；其次是核方法理论的发展，它独立于SVM本身，这也同时是SVM的一大优点；最后是最优化理论的发展，它同样与SVM具有相对独立性；套个流行话，三者是相辅相成、互相促进的。本文所提到的方法已经被很多人学习和研究过了，我这里做个简单介绍再加点自己的想法作为自己对学习SVM的一点总结吧。

2、背景知识

关于SVM的基础理论在先前的系列文章中已经有所体现了，Sequential Minimal Optimization(之后就用其简写SMO了)所解决的是支持向量机C-SVC模型，就是之前SVM学习——软间隔优化一文中提到的SVM模型，从这个名字也可以看出，这个模型的主要功能是分类，它有一个需要调节的参数C，以一阶软间隔优化为例，模型如下：

$max \quad \quad W(\alpha)=\sum\limits_{i=1}^{n}\alpha-\frac{1}{2}\sum\limits_{i,j=1}^{n}{y_iy_j\alpha_i\alpha_j(K(x_i,x_j))$

$s.t.$ $\sum\limits_{i=1}^{n}y_i\alpha_i=0$

$0 \leq \alpha_i \leq C$ $(i=1,2,...n)$

SMO就是要解这个凸二次规划问题，这里的C是个很重要的参数，它从本质上说是用来折中经验风险和置信风险的，C越大，置信风险越大，经验风险越小；并且所有的 $\alpha$ 因子都被限制在了以C为边长的大盒子里。SMO的出现使得我们不必去求助于昂贵的第三方工具去解决这个凸二次规划问题，目前对它的改进版本很多，我这里就介绍它的最初形式和思想。

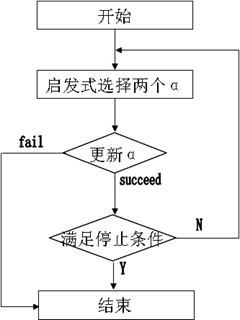
SMO是Microsoft Research的John C. Platt在《Sequential Minimal Optimization:A Fast Algorithm for Training Support Vector Machines》一文中提出的，作者信息：http://research.microsoft.com/en-us/people/jplatt/，其基本思想是将Vapnik在1982年提出的Chunking方法推到极致，即：通过将原问题分解为一系列小规模凸二次规划问题而获得原问题解的方法，每次迭代只优化由2个点组成的工作集，SMO算法每次启发式地选择两个 $\alpha$ 因子同时固定其它因子来找到这两个 $\alpha$ 因子的最优值，直到达到停止条件。

3、算法详述

(1)、 KKT条件

SMO是以C-SVC的KKT条件为基础进行后续操作的，这个KKT条件是：

$\alpha_i=0 \Leftrightarrow y_iu_i \geq 1$

$0 \leq \alpha_i \leq C \Leftrightarrow y_iu_i = 1$

$\alpha_i=C \Leftrightarrow y_iu_i \leq 1$

其中 $u_i=<w,x_i>+b$

上述条件其实就是KT互补条件，SVM学习——软间隔优化一文，有如下结论：

$\alpha_i(y_i(<w,x_i />+b)- 1+\xi_i)=0$ $(i=1,2,...n)$

$\mu_i\xi_i=(\alpha_i-C)\xi_i=0$ $(i=1,2,...n)$

从上面式子可以得到的信息是：当 $\alpha_i=C$ 时，松弛变量 $\xi_i \geq 0$ ，此时有： $y_i(<w,x_i />+b)= 1-\xi_i \Rightarrow y_i(<w,x_i>+b) \leq 1 \Rightarrow y_iu_i \leq 1$ ，对应样本点就是误分点；当 $\alpha_i=0$ 时，松弛变量 $\xi_i$ 为零，此时有 $y_i(<w,x_i />+b) \geq 1 \Rightarrow y_iu_i \geq 1$ ，对应样本点就是内部点，即分类正确而又远离最大间隔分类超平面的那些样本点；而 $0 < \alpha_i <C$ 时，松弛变量 $\xi_i$ 为零，有 $y_i(<w,x_i />+b) = 1 \Rightarrow y_iu_i = 1$ ，对应样本点就是支持向量。

(2)、凸优化问题停止条件

对于凸优化问题，在实现时总需要适当的停止条件来结束优化过程，停止条件可以是：

1、监视目标函数 $W(\alpha)$ 的增长率，在它低于某个容忍值时停止训练，这个条件是最直白和简单的，但是效果不好；

2、监视原问题的KKT条件，对于凸优化来说它们是收敛的充要条件，但是由于KKT条件本身是比较苛刻的，所以也需要设定一个容忍值，即所有样本在容忍值范围内满足KKT条件则认为训练可以结束；

3、监视可行间隙，它是原始目标函数值和对偶目标函数值的间隙，对于凸二次优化来说这个间隙是零，以一阶范数软间隔为例：

原始目标函数 $O(w,b)$ 与对偶目标函数 $W(\alpha)$ 的差为：

$Gap=\frac{1}{2}<w,w />+C\sum\limits_{i=1}^{n}\xi_i-( \sum\limits_{i=1}^{n}\alpha-\frac{1}{2}\sum\limits_{i,j=1}^{n}{y_iy_j\alpha_i\alpha_j(K(x_i,x_j)))$

$=\frac{1}{2}\sum\limits_{i,j=1}^{n}{y_iy_j\alpha_i\alpha_jK(x_i,x_j)+C\sum\limits_{i=1}^{n}\xi_i-( \sum\limits_{i=1}^{n}\alpha_i-\frac{1}{2}\sum\limits_{i,j=1}^{n}{y_iy_j\alpha_i\alpha_j(K(x_i,x_j)))$

$=\sum\limits_{i,j=1}^{n}{y_iy_j\alpha_i\alpha_jK(x_i,x_j)+C\sum\limits_{i=1}^{n}\xi_i- \sum\limits_{i=1}^{n}\alpha_i$

$=2 \sum\limits_{i=1}^{n}\alpha_i -2W(\alpha)+C\sum\limits_{i=1}^{n}\xi_i- \sum\limits_{i=1}^{n}\alpha_i$

$= \sum\limits_{i=1}^{n}\alpha_i -2W(\alpha)+C\sum\limits_{i=1}^{n}\xi_i$

定义比率：

$\frac{O(w,b)-W(\alpha)}{O(w,b)+1)}$ ，可以利用这个比率达到某个容忍值作为停止条件。

(3)、SMO思想

沿袭分解思想，固定“Chunking工作集”的大小为2，每次迭代只优化两个点的最小子集且可直接获得解析解，算法流程：

(4)、仅含两个Langrange乘子解析解

为了描述方便定义如下符号：

$K_{ij}=K(\mathbf{x_i}, \mathbf{x_j})$

$f(\mathbf{x_i})=\sum_{j=1}^n y_i \alpha_i K_{ij} + b$

$v_i=\sum_{j=3}^n y_j \alpha_j K_{ij} =f(\mathbf{x_i})-\sum_{j=1}^2 y_j \alpha_j K_{ij} - b$

于是目标函数就变成了：

$W(\alpha_2) =\sum_{i=1}^n \alpha_i - \frac12 \sum_{i=1}^n \sum_{j=1}^n y_i y_j K(x_i, x_j) \alpha_i \alpha_j \\$

$=\alpha_1+\alpha_2+ \sum_{i=3}^n \alpha_i-\frac{1}{2}\sum_{i=1}^n(\sum_{j=1}^2y_iy_j\alpha_i\alpha_jK{(x_ix_j)}+\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK{(x_ix_j)})$

$=\alpha_1+\alpha_2+ \sum_{i=3}^n \alpha_i-\frac{1}{2}\sum_{i=1}^2(\sum_{j=1}^2y_iy_j\alpha_i\alpha_jK{(x_ix_j)}+\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK{(x_ix_j)})$

$-\frac{1}{2}\sum_{i=3}^n(\sum_{j=1}^2y_iy_j\alpha_i\alpha_jK{(x_ix_j)}+\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK{(x_ix_j)})$

$=\alpha_1+\alpha_2+ \sum_{i=3}^n \alpha_i-\frac{1}{2}\sum_{i=1}^2\sum_{j=1}^2y_iy_j\alpha_i\alpha_jK{(x_ix_j)}-\sum_{i=1}^2\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK{(x_ix_j)}$

$-\frac{1}{2}\sum_{i=3}^n\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK{(x_ix_j)}$

$=\alpha_1+\alpha_2-\frac12 K_{11} \alpha_1^2 - \frac12 K_{22} \alpha_2^2 - y_1 y_2 K_{12} \alpha_1 \alpha_2 \\$

$-y_1\alpha_1\sum_{j=3}^ny_j\alpha_jK{(x_1x_j)}-y_2\alpha_2\sum_{j=3}^ny_j\alpha_jK{(x_2x_j)}$

$+ \sum_{i=3}^n \alpha_i-\frac{1}{2}\sum_{i=3}^n\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK{(x_ix_j)}$

$=\alpha_1+\alpha_2-\frac12 K_{11} \alpha_1^2 - \frac12 K_{22} \alpha_2^2 - y_1 y_2 K_{12} \alpha_1 \alpha_2 \\$

$- y_1 \alpha_1 v_1 - y_2 \alpha_2 v_2 + \text{constant} \$

注意第一个约束条件： $\sum_{i=1}^n y_i \alpha_i = 0$ ，可以将 $\alpha_3, \ldots, \alpha_n, y_3, \ldots, y_n$ 看作常数，有 $\alpha_1 y_1 + \alpha_2 y_2 = C^'$ ( $C^'$ 为常数，我们不关心它的值)，等式两边同时乘以 $y_1$ ，得到 $\alpha_1 = \gamma - s \alpha_2$ （ $\gamma$ 为常数，其值为 $C^'y_1$ ，我们不关心它， $s = y_1 y_2 \$ ）。将 $\alpha_1$ 用上式替换则得到一个只含有变量 $\alpha_2$ 的求极值问题：

$W(\alpha_2) =\gamma - s \alpha_2 + \alpha_2 - \frac12 K_{11} (\gamma - s \alpha_2)^2 - \frac12 K_{22} \alpha_2^2 \\$

$- s K_{12} (\gamma - s \alpha_2)\alpha_2 - y_1(\gamma - s \alpha_2)v_1 - y_2 \alpha_2 v_2 + \text{constant}$

这下问题就简单了，对 $\alpha_2$ 求偏导数得到：

$\frac{\partial W(\alpha_2)}{\partial \alpha_2} = -s + 1 + s K_{11} \gamma - K_{11} \alpha_2 - K_{22}\alpha_2 -s\gamma K_{12}+ 2K_{12}\alpha_2 + y_2v_1 - y_2 v_2 = 0$

将 $y_2^2=1$ 、 $s=y_1y_2$ 带入上式有：

$\alpha_2^{new} = \frac{y_2(y_2 - y_1 + y_1 \gamma (K_{11}-K_{12})+v_1-v_2)}{K_{11}+K_{22}-2K_{12}}$

带入 $v_i$ 、 $\gamma =\alpha_1^{old} + s \alpha_2^{old}$ ，用 $E_i = f(\mathbf{x}_i) - y_i$ ，表示误差项(可以想象，即使分类正确， $f(x_i)$ 的值也可能很大)、 $\eta = K_{11}+K_{22}-2K_{12} \ = ||\Phi(x_1)-\Phi(x_2)||^2$ ( $\Phi$ 是原始空间向特征空间的映射)，这里 $\sqrt {\eta }$ 可以看成是一个度量两个样本相似性的距离，换句话说，一旦选择核函数则意味着你已经定义了输入空间中元素的相似性。

最后得到迭代式：

$\alpha_2^{new} = \alpha_2^{old} + \frac{y_2(E_1-E_2)}{\eta}$

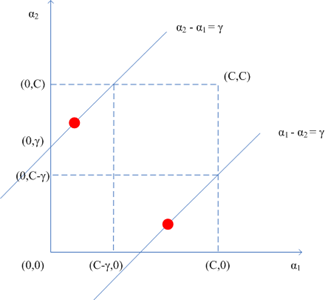
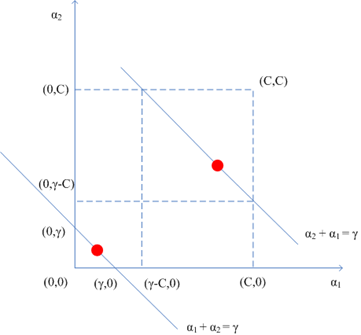
注意第二个约束条件——那个强大的盒子： $0 \leq \alpha_i \leq C$ ，这意味着 $\alpha_2^{new}$ 也必须落入这个盒子中，综合考虑两个约束条件，下图更直观：

$y_1$ 和 $y_2$ 异号的情形

$y_1$ 和 $y_2$ 同号的情形

可以看到 $\alpha_1, \alpha_2$ 两个乘子既要位于边长为C的盒子里又要在相应直线上，于是对于 $\alpha_2$ 的界来说，有如下情况：

$\begin{cases} \ L=max{\left\{0, \alpha_2^{old} - \alpha_1^{old}\right\}} \quad \quad \quad & y_1y_2 = -1, \\ \ L=max{\left\{0, \alpha_1^{old} + \alpha_2^{old} - C \right\}}& y_1y_2 = 1, \end{cases$ $\begin{cases} \ H=min{\left\{C, C + \alpha_2^{old} - \alpha_1^{old}\right\}} \quad \quad & y_1y_2 = -1\\ \ H=min{\left\{C, \alpha_1^{old} + \alpha_2^{old} \right\}}& y_1y_2 = 1 \end{cases}$

整理得下式：

$\alpha_2^{new,clipped} = \begin{cases} \ L \quad \quad \quad & \alpha_2^{new} \leq L\\ \ \alpha_2^{new} \quad \quad \quad & L< \alpha_2^{new} < H\\ \ H \quad & \alpha_2^{new} \geq H \end{cases}$

又因为 $\alpha_1^{old} = \gamma - s \alpha_2 ^{old}$ ， $\alpha_1^{new} = \gamma - s \alpha_2 ^{new,clipped}$ ，消去 $\gamma$ 后得到：

$\alpha_1^{new}=\alpha_1^{old}+y_1y_2(\alpha_2^{old}-\alpha_2^{new,clipped})$

(5)、启发式的选择方法

根据选择的停止条件可以确定怎么样选择点能对算法收敛贡献最大，例如使用监视可行间隙的方法，一个最直白的选择就是首先优化那些最违反KKT条件的点，所谓违反KKT条件是指：

$\alpha_i=0 \quad \quad \quad && \quad \quad \quad y_iu_i<1$

$0 \leq \alpha_i \leq C \quad \quad \quad && \quad \quad \quad y_iu_i \neq 1$

$\alpha_i=C \quad \quad \quad && \quad \quad \quad y_iu_i /> 1$

由前面的停止条件3可知，对可行间隙贡献最大的点是那些

$Gap_i=\alpha_i(y_i(\sum\limits_{j=1}^{n}\alpha_jy_iK(x_i,x_j))-1)+C\xi_i=\alpha_i(y_iu_i-1-y_ib))+C\xi_i$

其中， $\xi_i=max(0,1-y_iu_i)$

取值大的点，这些点导致可行间隙变大，因此应该首先优化它们，原因如下：

1、当满足KKT条件：即 $\alpha_i=0 \Leftrightarrow y_iu_i \geq 1$ 时， $Gap_i=\alpha_i(y_iu_i-1-y_ib))+C\xi_i =0$

当违背KKT条件：即 $\alpha_i=0 \quad \quad && \quad \quad y_iu_i<1$ 时， $\xi_i />0$ ，于是 $Gap_i=\alpha_i(y_iu_i-1-y_ib))+C\xi_i />0$

可见，由于违背KKT条件导致可行间隙变大；

2、当满足KKT条件：即 $0 \leq \alpha_i \leq C \Leftrightarrow y_iu_i = 1$ 时， $Gap_i=\alpha_i(y_iu_i-1-y_ib))+C\xi_i =-\alpha_iy_ib$

当违背KKT条件：即 $0 \leq \alpha_i \leq C \quad && \quad y_iu_i \neq 1$ 时

若 $y_iu_i>1$ 则 $\xi_i=0$ 且 $Gap_i=\alpha_i(y_iu_i-1-y_ib))+C\xi_i =\alpha_i(y_iu_i-1)-\alpha_iy_ib$ ，其中 $\alpha_i(y_iu_i-1) />0$

若 $y_iu_i<1$ 则 $\xi_i=1-y_iu_i$ 且 $Gap_i=\alpha_i(y_iu_i-1-y_ib))+C(1-y_iu_i) =(C-\alpha_i)(1-y_iu_i)-\alpha_iy_ib$ ，其中 $(C-\alpha_i)(1-y_iu_i) />0$

可见，由于违背KKT条件依然导致可行间隙变大；

3、当满足KKT条件：即 $\alpha_i=C \Leftrightarrow y_iu_i \leq 1$ 时， $Gap_i=\alpha_i(y_iu_i-1-y_ib))+C\xi_i =-Cy_ib$

当违背KKT条件：即 $\alpha_i=C \quad \quad \quad && \quad \quad \quad y_iu_i /> 1$ 时， $\xi_i=0$ 且 $Gap_i=\alpha_i(y_iu_i-1-y_ib))+C\xi_i =C(y_iu_i-1)-Cy_ib$ ，其中 $C(y_iu_i-1)>0$

可见，由于违背KKT条件还是会导致可行间隙变大。

SMO的启发式选择有两个策略：

启发式选择1：

最外层循环，首先，在所有样本中选择违反KKT条件的一个乘子作为最外层循环，用“启发式选择2”选择另外一个乘子并进行这两个乘子的优化，接着，从所有非边界样本中选择违反KKT条件的一个乘子作为最外层循环，用“启发式选择2”选择另外一个乘子并进行这两个乘子的优化(之所以选择非边界样本是为了提高找到违反KKT条件的点的机会)，最后，如果上述非边界样本中没有违反KKT条件的样本，则再从整个样本中去找，直到所有样本中没有需要改变的乘子或者满足其它停止条件为止。

启发式选择2：

内层循环的选择标准可以从下式看出：

$\alpha_2^{new} = \alpha_2^{old} + \frac{y_2(E_1-E_2)}{\eta}$

要加快第二个乘子的迭代速度，就要使 $\alpha_2^{old} + \frac{y_2(E_1-E_2)}{\eta}$ 最大，而在 $\eta$ 上没什么文章可做，于是只能使 $|E_1-E_2|$ 最大。

确定第二个乘子方法：

        1、首先在非界乘子中寻找使得 $|E_1-E_2|$ 最大的样本；
        2、如果1中没找到则从随机位置查找非界乘子样本；
        3、如果2中也没找到，则从随机位置查找整个样本(包含界上和非界乘子)。

(6)、关于两乘子优化的说明

由式子

$\frac{\partial W(\alpha_2)}{\partial \alpha_2} = -s + 1 + s K_{11} \gamma - K_{11} \alpha_2 - K_{22}\alpha_2 -s\gamma K_{12}+ 2K_{12}\alpha_2 + y_2v_1 - y_2 v_2$

可知：

$\frac{\partial W^2(\alpha_2)}{\partial \alpha_2^2} = - K_{11} - K_{22}+ 2K_{12}=-\eta$

于是对于这个单变量二次函数而言,如果其二阶导数 $-\eta < 0$ ，则二次函数开口向下，可以用上述迭代的方法更新乘子，如果 $-\eta \geq 0$ ，则目标函数只能在边界上取得极值(此时二次函数开口向上)，换句话说，SMO要能处理 $\eta$ 取任何值的情况，于是在 $-\eta \geq 0$ 时有以下式子：

1、 $\alpha_2^{new,clipped}=L$ 时：

$\alpha_1^{new}= \alpha_1^{old}+s(\alpha_2^{old}-L)$

2、 $\alpha_2^{new,clipped}=H$ 时：

$\alpha_1^{new}= \alpha_1^{old}+s(\alpha_2^{old}-H)$

3、 $W(\alpha_1,\alpha_2) =\sum_{i=1}^n \alpha_i - \frac12 \sum_{i=1}^n \sum_{j=1}^n y_i y_j K(x_i, x_j) \alpha_i \alpha_j \\$

$=\alpha_1+\alpha_2-\frac12 K_{11} \alpha_1^2 - \frac12 K_{22} \alpha_2^2 - y_1 y_2 K_{12} \alpha_1 \alpha_2 - y_1 \alpha_1 v_1 - y_2 \alpha_2 v_2 + \text{constant} \$

$=\alpha_1(1-y_1v_1)+\alpha_2(1-y_2v_2)-\frac12 K_{11} \alpha_1^2 - \frac12 K_{22} \alpha_2^2 - y_1 y_2 K_{12} \alpha_1 \alpha_2 + \text{constant} \$

$=\alpha_1y_1(y_1-(f(x_1)-\alpha_1y_1K_{11}-\alpha_2y_2K_{12}-b))+\alpha_2y_2(y_2-(f(x_2)-\alpha_1y_1K_{12}-\alpha_2y_2K_{22}-b))$

$-\frac12 K_{11} \alpha_1^2 - \frac12 K_{22} \alpha_2^2 - y_1 y_2 K_{12} \alpha_1 \alpha_2 + \text{constant} \$

$=\alpha_1^{new}(y_1(b-E_1)+\alpha_1^{old}K_{11}+s\alpha_2^{old}K_{12})+ \alpha_2^{new,clipped}(y_2(b-E_2)+\alpha_2^{old}K_{22}+s\alpha_1^{old}K_{12})$

$-\frac12 K_{11} \alpha_1^{new^{2}} - \frac12 K_{22} \alpha_2^{new,clipped^2} - y_1 y_2 K_{12} \alpha_1^{new} \alpha_2^{new,clipped} + \text{constant} \$

分别将乘子带入得到两种情况下的目标函数值： $W_L$ 和 $W_H$ 。显然，哪种情况下目标函数值最大，则乘子就往哪儿移动，如果目标函数的差在某个指定精度范围内，说明优化没有进展。

另外发现，每一步迭代都需要计算输出 $u$ 进而得到 $E$ ，于是还要更新阈值 $b$ ，使得新的乘子 $\alpha_1$ 、 $\alpha_2$ 满足KKT条件，考虑 $\alpha_1$ 、 $\alpha_2$ 至少有一个在界内，则需要满足 $0 \leq \alpha_i \leq C \Leftrightarrow y_iu_i = 1$ ，于是 $b$ 的迭代可以这样得到：

1、设 $\alpha_1 ^{new}$ 在界内，则：

$y_1u_1^{new}=1 \Rightarrow y_1(\alpha_1^{new}y_1K_{11}+\alpha_2^{new,clipped}y_2K_{21}+\sum \limit_{i=3}^{n}(\alpha_iy_iK_{i1})+b^{new})=1$

又因为：

$E_1=\alpha_1^{old}y_1K_{11}+\alpha_2^{old}y_2K_{21}+\sum \limit_{i=3}^{n}(\alpha_iy_iK_{i1})+b^{old}-y_1$ $\Rightarrow \sum \limit_{i=3}^{n}(\alpha_iy_iK_{i1})=E_1-\alpha_1^{old}y_1K_{11}-\alpha_2^{old}y_2K_{21}-b^{old}+y_1$

于是有：

$y_1(\alpha_1^{new}y_1K_{11}+\alpha_2^{new,clipped}y_2K_{21}+\sum \limit_{i=3}^{n}(\alpha_iy_iK_{i1})+b^{new})$

$=y_1(\alpha_1^{new}y_1K_{11}+\alpha_2^{new,clipped}y_2K_{21}+E_1-\alpha_1^{old}y_1K_{11}-\alpha_2^{old}y_2K_{21}-b^{old}+y_1+b^{new})= 1$

等式两边同乘 $y_1$ 后移项得：

$b^{new}=-\alpha_1^{new}y_1K_{11}-\alpha_2^{new,clipped}y_2K_{21}-E_1+\alpha_1^{old}y_1K_{11}+\alpha_2^{old}y_2K_{21}+b^{old}$

$=(\alpha_1^{old}-\alpha_1^{new})y_1K_{11}+(\alpha_2^{old}-\alpha_2^{new,clipped})y_2K_{21}-E_1+b^{old}$ ；

2、设 $\alpha_2^{new,clipped}$ 在界内，则：

$b^{new} =(\alpha_1^{old}-\alpha_1^{new})y_1K_{12}+(\alpha_2^{old}-\alpha_2^{new,clipped})y_2K_{22}-E_2+b^{old}$ ；

3、设 $\alpha_1 ^{new}$ 、 $\alpha_2^{new,clipped}$ 都在界内，则：情况1和情况2的 $b$ 值相等，任取一个；

4、设 $\alpha_1 ^{new}$ 、 $\alpha_2^{new,clipped}$ 都不在界内，则： $b^{new}$ 取值为情况1和情况2之间的任意值。

(7)、提高SMO的速度

从实现上来说，对于标准的SMO能提高速度的地方有：

1、能用缓存的地方尽量用，例如，缓存核矩阵，减少重复计算，但是增加了空间复杂度；

2、如果SVM的核为线性核时候，可直接更新 $w$ ，毕竟每次计算 $w=\sum\limits_{i=1}^n y_i\alpha_ix_i$ 的代价较高，于是可以利用旧的乘子信息来更新 $w$ ，具体如下：

$w^{new}=w^{old}+(\alpha_1^{new}-\alpha_1^{old})y_1x_1 +(\alpha_2^{new}-\alpha_2^{old})y_2x_2$ ，应用到这个性质的例子可以参见SVM学习——Coordinate Desent Method。

3、关注可以并行的点，用并行方法来改进，例如可以使用MPI，将样本分为若干份，在查找 $|E_1-E_2|$ 最大的乘子时可以现在各个节点先找到局部最大点，然后再从中找到全局最大点；又如停止条件是监视对偶间隙，那么可以考虑在每个节点上计算出局部可行间隙，最后在master节点上将局部可行间隙累加得到全局可行间隙。

对标准SMO的改进有很多文献，例如使用“Maximal Violating Pair ”去启发式的选择乘子是一种很有效的方法，还有使用“ Second Order Information”的方法，我觉得理想的算法应该是：算法本身的收敛速度能有较大提高，同时算法可并行程度也较高。

4、算法实现

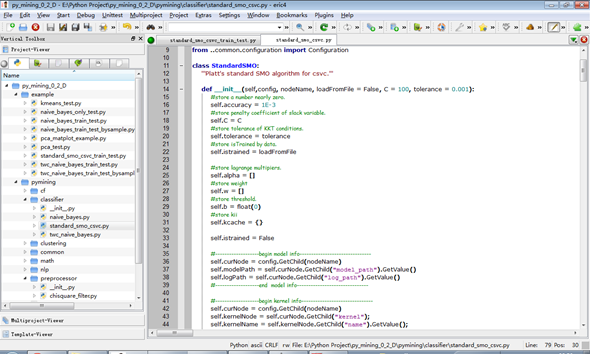
以cowman望达兄的PyMing-v0.2为平台做一个简单的实现，初学python，写的比较烂，拍砖时候轻点哈，貌似目前PyMing支持python3.0以下版本，开发python代码我使用的工具是：(python-2.6)+(PyQt-Py2.6-x86-gpl-4.8.4-1)+(Eric4-4.4.14 )，用Eric的最大好处是调试方便和智能感知做的比较好，安装很简单，先装python-2.6、再装PyQt(不停的点下一步)、最后装Eric，建立一个项目如图：

实现思路就是platt的那段伪码，需要加三个文件，py_mining_0_2_D\pymining\classifier里加一个分类器standard_smo_csvc；py_mining_0_2_D\example里加一个测试的例子standard_smo_csvc_train_test；py_mining_0_2_D\example\conf里改一下配置文件test。

1、standard_smo_csvc.py

import math

    import pickle

    import random

    from ..math.matrix import Matrix

    from ..math.text2matrix import Text2Matrix

    from ..nlp.segmenter import Segmenter

    from ..common.global_info import GlobalInfo

    from ..common.configuration import Configuration

    class StandardSMO:

        '''Platt's standard SMO algorithm for csvc.'''

        def __init__(self,config, nodeName, loadFromFile = False, C = 100, tolerance = 0.001):

            #store a number nearly zero.

            self.accuracy = 1E-3

            #store penalty coefficient of slack variable.

            self.C = C

            #store tolerance of KKT conditions.

            self.tolerance = tolerance        

            #store isTrained by data.

            self.istrained = loadFromFile

            #store lagrange multipiers.

            self.alpha = []

            #store weight

            self.w = []

            #store threshold.

            self.b = float(0)        

            #store kii

            self.kcache = {}

            self.istrained = False

            #-------------------begin model info-------------------------------

            self.curNode = config.GetChild(nodeName)

            self.modelPath = self.curNode.GetChild("model_path").GetValue()

            self.logPath = self.curNode.GetChild("log_path").GetValue()

            #-------------------end  model info-------------------------------

            #-------------------begin kernel info-------------------------------

            self.curNode = config.GetChild(nodeName)

            self.kernelNode = self.curNode.GetChild("kernel");

            self.kernelName = self.kernelNode.GetChild("name").GetValue();

            #to get parameters from top to button -> from left to right -> from inner to outer.        

            self.parameters = self.kernelNode.GetChild("parameters").GetValue().split(',');

            #-------------------end  kernel info-------------------------------

            if (loadFromFile):

                f = open(self.modelPath, "r")

                modelStr = pickle.load(f)

                [self.alphay, self.sv, self.b, self.w] = pickle.loads(modelStr)

                f.close()

                self.istrained = True

        def DotProduct(self,i1,i2):

            '''To get vector's dot product for training.'''

            dot = float(0)

            for i in range(0,self.trainx.nCol):

                dot += self.trainx.Get(i1,i) * self.trainx.Get(i2,i)  

            return dot

        def Kernel(self):

            '''To get kernel function with configuration for training.

                kernel function includes RBF,Linear and so on.'''      

            if self.kernelName == 'RBF':

                return lambda xi,yi: math.exp((2*self.DotProduct(xi,yi)-self.DotProduct(xi,xi)-self.DotProduct(yi,yi))/(2*float(self.parameters[0])*float(self.parameters[0])))

            elif self.kernelName == 'Linear':

                return lambda xi,yi:self.DotProduct(xi,yi) + float(self.parameters[0])

            elif self.kernelName == 'Polynomial':

                return lambda xi,yi: (float(self.parameters[0]) * self.DotProduct(xi,yi) + float(self.parameters[1])) ** int(self.parameters[2])

        def DotVectorProduct(self,v1,v2):

            '''To get vector's dot product for testing.'''

            if len(v1) != len(v2):

                print 'The dimensions of two vector should equal'

                return 0.0

            dot = float(0)

            for i in range(0,len(v1)):

                dot += v1[i] * v2[i]

            return dot

        def KernelVector(self, v1, v2):

            '''To get kernel function for testing.'''

            if self.kernelName == 'RBF':

                return math.exp((2*self.DotVectorProduct(v1, v2)-self.DotVectorProduct(v1, v1)-self.DotVectorProduct(v2, v2))/(2*float(self.parameters[0])*float(self.parameters[0])))

            elif self.kernelName == 'Linear':

                return self.DotVectorProduct(v1, v2) + float(self.parameters[0])

            elif self.kernelName == 'Polynomial':

                return (float(self.parameters[0]) * self.DotVectorProduct(v1,v2) + float(self.parameters[1])) ** int(self.parameters[2])

        def F(self,i1):

            '''To calculate output of an sample.

                return output.'''

            if self.kernelName == 'Linear':

                dot = 0

                for i in range(0,self.trainx.nCol):

                    dot += self.w[i] * self.trainx.Get(i1,i);    

                return dot + self.b

            K = self.Kernel()   

            final = 0.0

            for i in range(0,len(self.alpha)):

                if self.alpha[i] > 0:

                    key1 = '%s%s%s'%(str(i1), '-', str(i))

                    key2 = '%s%s%s'%(str(i), '-', str(i1))

                    if self.kcache.has_key(key1):

                        k = self.kcache[key1]

                    elif self.kcache.has_key(key2):

                        k = self.kcache[key2]

                    else:

                        k =  K(i1,i)

                        self.kcache[key1] = k

                    final += self.alpha[i] * self.trainy[i] * k

            final += self.b

            return final

        def examineExample(self,i1):

            '''To find the first lagrange multipliers.

                    then find the second lagrange multipliers.'''

            y1 = self.trainy[i1]

            alpha1 = self.alpha[i1]

            E1 = self.F(i1) - y1

            kkt = y1 * E1

            if (kkt > self.tolerance and kkt > 0) or (kkt <- self.tolerance and kkt < self.C):#not abide by KKT conditions

                if self.FindMaxNonbound(i1,E1):

                    return 1

                elif self.FindRandomNonbound(i1):

                    return 1

                elif self.FindRandom(i1):

                    return 1

            return 0

        def FindMaxNonbound(self,i1,E1):

            '''To find second lagrange multipliers from non-bound.

                condition is maximum |E1-E2| of non-bound lagrange multipliers.'''

            i2 = -1

            maxe1e2 = None

            for i in range(0,len(self.alpha)):

                if self.alpha[i] > 0 and self.alpha[i] < self.C:

                    E2 = self.F(i) - self.trainy[i]

                    tmp = math.fabs(E1-E2)

                    if maxe1e2 == None or maxe1e2 < tmp:

                        maxe1e2 = tmp

                        i2 = i

            if i2 >= 0 and self.StepOnebyOne(i1,i2) :

                return  1              

            return 0

        def FindRandomNonbound(self,i1):

            '''To find second lagrange multipliers from non-bound.

                condition is random of non-bound lagrange multipliers.'''

            k = random.randint(0,len(self.alpha)-1)

            for i in range(0,len(self.alpha)):

                i2 = (i + k)%len(self.alpha)

                if self.alpha[i2] > 0 and self.alpha[i2] < self.C and self.StepOnebyOne(i1,i2):

                    return 1

            return 0

        def FindRandom(self,i1):

            '''To find second lagrange multipliers from all.

                condition is random one of all lagrange multipliers.'''

            k = random.randint(0,len(self.alpha)-1)

            for i in range(0,len(self.alpha)):

                i2 = (i + k)%len(self.alpha)

                if self.StepOnebyOne(i1,i2):

                    return 1

            return 0

        def W(self,alpha1new,alpha2newclipped,i1,i2,E1,E2, k11, k22, k12):

            '''To calculate W value.'''

            K = self.Kernel()

            alpha1 = self.alpha[i1]

            alpha2 = self.alpha[i2]

            y1 = self.trainy[i1]

            y2 = self.trainy[i2]

            s = y1 * y2

            w1 = alpha1new * (y1 * (self.b - E1) + alpha1 * k11 + s * alpha2 * k12)

            w1 += alpha2newclipped * (y2 * (self.b - E2) + alpha2 * k22 + s * alpha1 * k12)

            w1 = w1 - k11 * alpha1new * alpha1new/2 - k22 * alpha2newclipped * alpha2newclipped/2 - s * k12 * alpha1new * alpha2newclipped

            return w1

        def StepOnebyOne(self,i1,i2):

            '''To solve two lagrange multipliers problem.

                the algorithm can reference the blog.'''

            if i1==i2:

                return 0

            #to get kernel function.

            K = self.Kernel()

            alpha1 = self.alpha[i1]

            alpha2 = self.alpha[i2]

            alpha1new = -1.0

            alpha2new = -1.0

            alpha2newclipped = -1.0

            y1 = self.trainy[i1]

            y2 = self.trainy[i2]

            s = y1 * y2

            key11 = '%s%s%s'%(str(i1), '-', str(i1))

            key22 = '%s%s%s'%(str(i2), '-', str(i2))

            key12 = '%s%s%s'%(str(i1), '-', str(i2))

            key21 = '%s%s%s'%(str(i2), '-', str(i1))

            if self.kcache.has_key(key11):

                k11 = self.kcache[key11]

            else:

                k11 = K(i1,i1)

                self.kcache[key11] = k11    

            if self.kcache.has_key(key22):

                k22 = self.kcache[key22]

            else:

                k22 = K(i2,i2)

                self.kcache[key22] = k22

            if self.kcache.has_key(key12):

                k12 = self.kcache[key12]

            elif self.kcache.has_key(key21):

                k12 = self.kcache[key21]

            else:

                k12 = K(i1,i2)

                self.kcache[key12] = k12       

            eta = k11 + k22 - 2 * k12

            E1 = self.F(i1) - y1        

            E2 = self.F(i2) - y2                

            #to calucate bound.

            L = 0.0

            H = 0.0

            if y1*y2 == -1:

                gamma = alpha2 - alpha1

                if gamma > 0:

                    L = gamma

                    H = self.C

                else:

                    L = 0

                    H = self.C + gamma            

            if y1*y2 == 1:

                gamma = alpha2 + alpha1

                if gamma - self.C > 0:

                    L = gamma - self.C

                    H = self.C

                else:

                    L = 0

                    H = gamma

            if H == L:

                return 0

            #------------------------begin to move lagrange multipliers.----------------------------

            if -eta < 0:

                #to calculate apha2's new value

                alpha2new = alpha2 + y2 * (E1 - E2)/eta

                if alpha2new < L:

                    alpha2newclipped = L

                elif alpha2new > H:

                     alpha2newclipped = H

                else:

                    alpha2newclipped = alpha2new

            else:            

                w1 = self.W(alpha1 + s * (alpha2 - L),L,i1,i2,E1,E2, k11, k22, k12)

                w2 = self.W(alpha1 + s * (alpha2 - H),H,i1,i2,E1,E2, k11, k22, k12)

                if w1 - w2 > self.accuracy:

                    alpha2newclipped = L

                elif w2 - w1 > self.accuracy:

                    alpha2newclipped = H

                else:

                    alpha2newclipped = alpha2  

            if math.fabs(alpha2newclipped - alpha2) < self.accuracy * (alpha2newclipped + alpha2 + self.accuracy):

                return 0

            alpha1new = alpha1 + s * (alpha2 - alpha2newclipped)

            if alpha1new < 0:

                alpha2newclipped += s * alpha1new

                alpha1new = 0

            elif alpha1new > self.C:

                alpha2newclipped += s * (alpha1new - self.C)

                alpha1new = self.C

            #------------------------end   to move lagrange multipliers.----------------------------

            if alpha1new > 0 and alpha1new < self.C:

                self.b += (alpha1-alpha1new) * y1 * k11 + (alpha2 - alpha2newclipped) * y2 *k12 - E1

            elif alpha2newclipped > 0 and alpha2newclipped < self.C:

                self.b += (alpha1-alpha1new) * y1 * k12 + (alpha2 - alpha2newclipped) * y2 *k22 - E2

            else:

                b1 = (alpha1-alpha1new) * y1 * k11 + (alpha2 - alpha2newclipped) * y2 *k12 - E1 + self.b

                b2 = (alpha1-alpha1new) * y1 * k12 + (alpha2 - alpha2newclipped) * y2 *k22 - E2 + self.b

                self.b = (b1 + b2)/2

            if self.kernelName == 'Linear':

                for j in range(0,self.trainx.nCol):

                    self.w[j] += (alpha1new - alpha1) * y1 * self.trainx.Get(i1,j) + (alpha2newclipped - alpha2) * y2 * self.trainx.Get(i2,j)

            self.alpha[i1] = alpha1new

            self.alpha[i2] = alpha2newclipped

            print 'a', i1, '=',alpha1new,'a', i2,'=', alpha2newclipped

            return 1        

        def Train(self,trainx,trainy):

            '''To train samples.

                self.trainx is training matrix and self.trainy is classifying label'''

            self.trainx = trainx

            self.trainy = trainy

            if len(self.trainy) != self.trainx.nRow:

                print "ERROR!, x.nRow should == len(y)"

                return 0

            numChanged = 0;

            examineAll = 1;

            #to initialize all lagrange multipiers with zero.

            for i in range(0,self.trainx.nRow):

                self.alpha.append(0.0)

            #to initialize w with zero.

            for j in range(0,self.trainx.nCol):

                self.w.append(float(0))

            while numChanged > 0 or examineAll:

                numChanged=0

                print 'numChanged =', numChanged

                if examineAll:

                    for k in range(0,self.trainx.nRow):

                        numChanged += self.examineExample(k);#first time or all of lagrange multipiers are abide by KKT conditions then examin all samples.

                else:

                    for k in range(0,self.trainx.nRow):

                        if self.alpha[k] !=0 and self.alpha[k] != self.C:

                            numChanged += self.examineExample(k);#to examin all non-bound lagrange multipliers

                if(examineAll == 1):

                    examineAll = 0

                elif(numChanged == 0):

                    examineAll = 1

            else:

                #store support vector machine.                

                self.alphay = []

                self.index = []

                for i in range(0,len(self.alpha)):

                    if self.alpha[i] > 0:

                        self.index.append(i)

                        self.alphay.append(self.alpha[i] * self.trainy[i])

                self.sv = [[0 for j in range(self.trainx.nCol)]  for i in range(len(self.index))]

                for i in range(0, len(self.index)):

                    for j in range(0,self.trainx.nCol):

                        self.sv[i][j] = self.trainx.Get(self.index[i], j)

                #dump model path

                f = open(self.modelPath, "w")

                modelStr = pickle.dumps([self.alphay, self.sv, self.b, self.w], 1)

                pickle.dump(modelStr, f)

                f.close()   

                self.istrained = True

        def Test(self,testx,testy):

            '''To test samples.

                self.testx is training matrix and self.testy is classifying label'''    

            #check parameter

            if (not self.istrained):

                print "Error!, not trained!"

                return False

            if (testx.nRow != len(testy)):

                print "Error! testx.nRow should == len(testy)"

                return False

            self.trainx = testx

            self.trainy = testy

            correct = 0.0

            for i in range(0, self.trainx.nRow):

                fxi = 0.0

                rowvector = [self.trainx.Get(i, k) for k in range(0, self.trainx.nCol)]

                if self.kernelName == 'Linear':

                    fxi += self.KernelVector(self.w, rowvector) + self.b

                else:

                    for j in range(0, len(self.alphay)):                  

                        fxi += self.alphay[j] * self.KernelVector(self.sv[j], rowvector) 

                    fxi += self.b

                if fxi * self.trainy[i] >= 0:

                    correct +=1

                print 'output is', fxi, 'label is', self.trainy[i]

            print 'acu=', correct/len(self.trainy)

2、standard_smo_csvc_train_test

import sys, os

    import math

    sys.path.append(os.path.join(os.getcwd(), '../'))

    from pymining.math.matrix import Matrix

    from pymining.math.text2matrix import Text2Matrix

    from pymining.nlp.segmenter import Segmenter

    from pymining.common.global_info import GlobalInfo

    from pymining.common.configuration import Configuration

    from pymining.preprocessor.chisquare_filter import ChiSquareFilter

    from pymining.classifier.standard_smo_csvc import StandardSMO

    if __name__ == "__main__":

        config = Configuration.FromFile("conf/test.xml")

        GlobalInfo.Init(config, "__global__")

        txt2mat = Text2Matrix(config, "__matrix__")

        [trainx, trainy] = txt2mat.CreateTrainMatrix("data/train-csvc.txt")

        chiFilter = ChiSquareFilter(config, "__filter__")

        chiFilter.TrainFilter(trainx, trainy)

        [trainx, trainy] = chiFilter.MatrixFilter(trainx, trainy)

        nbModel = StandardSMO(config, "standard_smo_csvc")

        nbModel.Train(trainx, trainy)

        [trainx, trainy] = txt2mat.CreatePredictMatrix("data/train-csvc-test.txt")

        [trainx, trainy] = chiFilter.MatrixFilter(trainx, trainy)

        nbModel = StandardSMO(config, "standard_smo_csvc", True)

        nbModel.Test(trainx, trainy)

3、test.xml

<config>

      <__segmenter__>

        <main_dict>dict/dict.main</main_dict>

      </__segmenter__>

      <__matrix__>

      </__matrix__>

      <__global__>

        <term_to_id>mining/term_to_id</term_to_id>

        <id_to_term>mining/id_to_term</id_to_term>

        <id_to_doc_count>mining/id_to_doc_count</id_to_doc_count>

        <class_to_doc_count>mining/class_to_doc_count</class_to_doc_count>

        <id_to_idf>mining/id_to_idf</id_to_idf>

      </__global__>

      <__filter__>

        <rate>0.9</rate>

        <method>max</method>

        <log_path>mining/filter.log</log_path>

        <model_path>mining/filter.model</model_path>

      </__filter__>

      <naive_bayes>

        <model_path>mining/naive_bayes.model</model_path>

        <log_path>mining/naive_bayes.log</log_path>

      </naive_bayes>

      <twc_naive_bayes>

        <model_path>mining/naive_bayes.model</model_path>

        <log_path>mining/naive_bayes.log</log_path>

      </twc_naive_bayes>

      <standard_smo_csvc>

        <model_path>mining/standard_smo.model</model_path>

        <log_path>mining/standard_smo.log</log_path>

        <kernel>

          <name>RBF</name>

          <parameters>10</parameters>

        </kernel>

      </standard_smo_csvc>

    </config>

代码可以从这里获得

5、参考文献

1)、Platt(1998):http://research.microsoft.com/~jplatt/smoTR.pdf；

2)、《An Introduction to Support Vector Machines and Other Kernel-based Learning Methods》；

3)、Osuna等:An Improved Training Algorithm for Support Vector Machines；

4)、Keerthi et al.(2001): Improvements to Platt’s SMO algorithm for SVM classifier design；

5)、Fan,Chen,and Lin(2005): Working Set Selection Using Second Order Information；

6)、google

posted on 2011-06-01 23:15 Leo Zhang 阅读(14459) 评论(8) 编辑收藏举报

刷新页面返回顶部

Leo Zhang