SVM学习——核函数

还记得上篇末提到的对于优化问题：

$max \quad\quad\quad\quad W(\alph)=\sum\limits_{i=1}^{n}{\alph_i}-\frac{1}{2}\sum\limits_{i,j=1}^{n}{y_iy_j\alph_i\alph_j<x_i,x_j>}$

$s.t.\quad\quad\quad\quad \sum\limits_{i=1}^{n}{\alph_iy_i}=0$

$\alph_i \geq 0 \quad\quad\quad\quad i=1...n$

的求解需要计算 $<x_i,x_j>$ 这个内积，而如果输入样本线性不可分的话，我们采取的方法是通过 $\Phi:X->F$ 函数映射将输入样本映射到另外一个高维空间并使其线性可分。

以库克定律为例(http://zh.wikipedia.org/zh-cn/%E9%9D%99%E7%94%B5%E5%8A%9B)：

一个电量为 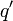$q'\,\!$ 的点电荷作用于另一个电量为 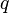$q\,\!$ 的点电荷，其静电力 $F\,\!$ 的大小，可以用方程表达为:

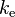$F = k_{\mathrm{e}}\frac{qq'}{r^2}\,\!$ ，其中， $r\,\!$ 是两个点电荷之间的距离， $k_{\mathrm{e}}\,\!$ 是库仑常数。

显然这个定律无法用线性学习器来表达，看到乘积想到ln函数，对原始形式两边取ln，得到：

$lnF(q,q^',r)=ln(k_e)+ln(q)+ln(q^')-2ln(r)$ ，令 $x=ln(q)$ ， $y=ln(q^')$ ， $z=ln(r)$ ， $k=in(k_e)$ ， $G(x,y,z)=ln(F(q,q^',r))$ ，那么就得到一个线性学习器：

$G(x,y,z)=k+x+y-2z$

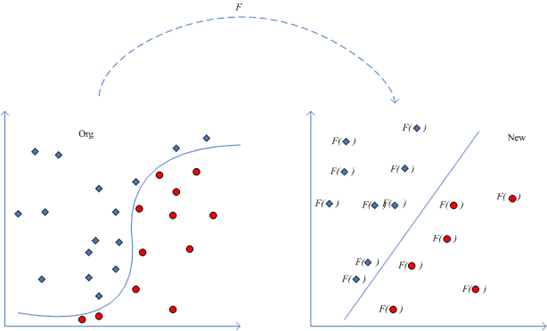
这个过程可以用下图说明：

这样就将内积 $<x_i,x_j>$ 就变成了 $<\Phi(x_i),\Phi(x_j)>$ 。

求 $<\Phi(x_i),\Phi(x_j)>$ 可以有两种方法：

1、先找到这种映射，然后将输入空间中的样本映射到新的空间中，最后在新空间中去求内积 $<\Phi(x_i),\Phi(x_j)>$ ；

2、或者是找到某种方法，它不需要显式的将输入空间中的样本映射到新的空间中而能够在输入空间中直接计算出内积 $<\Phi(x_i),\Phi(x_j)>$ 。

先看第一种方法，以多项式 $x_1+x_2+x_1^2+x_2^2+c=0$ 为例，对其进行变换， $c_1=x_1$ ， $c_2=x_2$ ， $c_3=x_1^2$ ， $c_4=x_2^2$ ，得到：

$c_1+c_2+c_3+c_4+c=0$ ，也就是说通过把输入空间从二维向四维映射后，样本由线性不可分变成了线性可分，但是这种转化带来的直接问题是维度变高了，这意味着，首先可能导致后续计算变复杂，其次可能出现维度之咒，对于学习器而言就是：特征空间维数可能最终无法计算，而它的泛化能力(学习器对训练样本以外数据的适应性)会随着维度的增长而大大降低，这也违反了“奥坎姆的剃刀”，最终可能会使得内积 $<\Phi(x_i),\Phi(x_j)>$ 无法求出，于是也就失去了这种转化的优势了；

再看第二种方法，它其实是对输入空间向高维空间的一种隐式映射，它不需要显式的给出那个映射，在输入空间就可以计算 $<\Phi(x_i),\Phi(x_j)>$ ，这就是传说中的核函数方法：

定义1:核是一个函数 $K$ ，对于所有的 $x_1,x_2 \in X$ 满足， $K<x_1,x_2>=<\Phi(x_1),\Phi(x_2)>$ ，这里的 $\Phi$ 为从 $X$ 到内积特征空间 $F$ 的映射。

于是输入空间的标准内积就被推广了。

$K(x,y)$ 什么时候才是核函数呢？

假设有输入空间 $X={x_1,x_2,....x_n}$ 且 $K(x,y)$ 为对称函数，那么对于所有样本得到下面矩阵： $k=(K(x_i,x_j))\quad\quad(i,j=0,...n)$ ，显然，这个是个对称矩阵，那么对于对称矩阵一定存在一个正交矩阵，使得 $P^TkP=\Lambda$ ，这里 $\Lambda$ 是包含k的特征值 $\lambda_i$ 的对角矩阵，特征值 $\lambda_i$ 对应的特征向量为 $v_t=(v_{t1},v_{t2},...v_{tn})^T$ ，其中n为样本数，对输入空间做如下映射 $\phi$ ：

$\phi:x_i|->(\sqrt{\lambda_1}v_{1i},\sqrt{\lambda_2}v_{2i}...\sqrt{\lambda_n}v_{tn})\quad\quad \in R^n(i=1,...n)$

于是有 $<\phi(x_i),\phi(x_j)>=\sum\limits_{t=1}^n{\lambda_tv_{ti}v_{tj}}=(V\Lambda V^T)_{i,j}=k_{i,j}=K(x_i,x_j)$ ，(其中 $V$ 为特征向量组成的矩阵， $\Lambda$ 为相应特征值组成的三角矩阵)，也就是说K是对应于映射 $\phi$ 的核函数。

例子：有 $k= \left[ \begin{array}{cccc} 4&0&0\\ 0&3&1\\ 0&1&3\\ \end{array}\right ]$ ，由 $|k-\lambda E|=0$ 解得特征值： $\lambda_1=\lambda_2=4$ ， $\lambda_3=2$ ，对2重特征根4求 $(A-4E)x=0$ 的基础解系、正交化、单位化后得到特征向量： $v_1=(1,0,0)^T$ 和 $v_2=(0,\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})^T$ ，对 $\lambda_3$ 的特征向量单位化后得到 $v_3=(0,-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})^T$ ，于是有 $V=(v_1,v_2,v_3)= \left[ \begin{array}{cccc} 1&0&0\\ 0&\frac{1}{\sqrt(2)}&-\frac{1}{\sqrt(2)}\\ 0&\frac{1}{\sqrt(2)}&\frac{1}{\sqrt(2)}\\ \end{array}\right ]$ ，满足 $V^{-1}kV=\Lambda=\left[ \begin{array}{cccc} 4&0&0\\ 0&4&0\\ 0&0&2\\ \end{array}\right ]$ ，对所有输入样本做映射得：

$\phi(x_1)=(\sqrt{4}*1,\sqrt{4}*0,\sqrt{2}*0)=(2,0,0)^T$ ；

$\phi(x_2)=(\sqrt{4}*0,\sqrt{4}*\frac{1}{\sqrt{2}},\sqrt{2}*(-\frac{1}{\sqrt{2}}))^T=(0,\sqrt{2},-1)$ ;

$\phi(x_3)=(\sqrt{4}*0,\sqrt{4}*\frac{1}{\sqrt{2}},\sqrt{2}*\frac{1}{\sqrt{2}})^T=(0,\sqrt{2},1)$ 。

随便选两个做内积，如 $<\phi(x_2),\phi(x_3)>=0*0+\sqrt{2}*\sqrt{2}+(-1)*1=1=k(x_2,x_3)$ 。

由此可见： $K(x,y)$ 就是对应于特征映射 $\phi$ 的核函数，也就得到下面的结论：

定理1：存在有限输入空间 $X$ ， $K(x,y)$ 为 $X$ 上的对称函数，那么 $K(x,y)$ 是核函数的充要条件是矩阵 $k=(K(x_i,x_j))\quad\quad(i,j=0,...n)$ 半正定，此时相当于对输入空间向特征空间进行了隐式的 $\phi$ 映射。对于上面的映射 $\phi$ ，令 $\phi_i(x_j)=\sqrt{\lambda_i}v_{ij}$ ，于是 $\phi(x)=(\phi_1(x),\phi_2(x),...\phi_n(x))$ ，进而 $K(x,y)=\sum\limits_{i=1}^\infty{\lambda_i\phi_i(x)\phi_i(y)}$ 。

定理3：设 $X$ 是 $R^n$ 的一个紧子集(闭合且有界子集)， $K(x,y)$ 为 $X$ 上的对称函数，如果它在希尔伯特空间上的积分算子 $T_kf(x)=f(t)dt$ 满足：

$\forall{f} \in L_2(X),\quad \quad \quad \int_{X \times X}{K(x,y)f(x)f(y)dxdy} \geq 0$

这里 $L_2$ 指的是由满足条件 $\int f(x)^2dx< \infty$ 的所有函数 $f(x)$ 组成的空间。

在 $X \times X$ 上扩展 $K(x,y)$ 到一个一致收敛的序列，该序列由 $T_k$ 的特征函数 $\phi_j \in L_2(x)$ 构成，归一化使得 $||\phi_j||_{L_2}=1$ ，且所有特征值 $\lambda_j \geq 0$ ，则核函数 $K(x,y)$ 可以被特征分解为：

$K(x,y)=\sum\limits_{i=1}^\infty{\lambda_i\phi_i(x)\phi_i(y)}$

在核方法中有一个相当重要的、不得不说的概念(先打个标记)：

定义2：设 $H$ 是希尔伯特函数空间，其元素是某个抽象集合 $X$ 上的实值或复值函数，如果对于任何 $y \in X$ ， $K(x,y)$ 作为 $x$ 的函数都是 $H$ 中的元素，而且对于任何 $y \in X$ 及 $f \in H$ 取内积有：
$f(y)=<f(x),K(x,y)>$

则 $H$ 称为为再生核希尔伯特空间(Reproducing Kernel Hilbert Space，RKHS)；称 $K(x,y)$ 为再生核空间 $H$ 的再生核(简称RK)。

定理4：对于定义在域 $X \subset R^d$ 上的每一个 $Mercer$ 核 $K(x,y)$ ，存在一个定义在 $X$ 上的函数的再生希尔伯特空间 $RKHS$ ，其中 $K$ 是再生核。反过来，对于线性有界函数的任意希尔伯特空间，存在再生核这个命题也成立。

当然也可以利用核函数来构造核函数，有时候这种构造会很有效的解决问题：

条件：设 $K_1(x,y)$ 、 $K_2(x,y)$ 是 $X \times X$ 上的核， $X \subseteq R^n$ ， $f$ 是 $X$ 上的实值函数， $\phi:X->R^m$ ， $K_3(x,y)$ 是 $R^m \times R^m$ 上的核， $A$ 是一个对称半正定矩阵，则下面的函数都是核：

1、 $K(x,y)=K_1(x,y)+K_2(x,y)$ ;

2、 $K(x,y)=\alph K_1(x,y)$ ;

3、 $K(x,y)=K_1(x,y)K_2(x,y)$ ;

4、 $K(x,y)=f(x)f(y)$ ;

5、 $K(x,y)=K_3(\phi(x),\phi(y))$ ;

6、 $K(x,y)=x^TAy$ 。

核的选择对于支持向量机至关重要，选定核 $K(x_i,x_j)$ 后，原问题就变成了：

$max \quad \quad \quad \sum\limits_{i=1}^{n} \alph_i-\frac{1}{2}\sum\limits_{i,j=1}^{n}y_iy_j\alph_i\alph_jK(x_i,x_j)$

$s.t.\quad\quad\quad\quad \sum\limits_{i=1}^{n}{\alph_iy_i}=0$

$\alph_i \geq 0 \quad\quad\quad\quad i=1...n$

这个优化问题有最优解么？记得核要满足Mercer条件，即矩阵 $k=(K(x_i,x_j))\quad\quad(i,j=0,...n)$ 在所有训练集上半正定，这说明这个优化是凸优化，于是这个条件保证了最大化间隔优化问题有唯一解，简直是天作之合啊，配合的天衣无缝；最后求的 $(\alph^*)$ 和 $b$ ，那么从输入空间向特征空间隐式映射后得到的最大间隔超平面也就出来了： $f(x)=\sum\limits_{i=1}^{n}\alph^*y_iK(x_i,x)+b^*$ ，且有几何间隔 $\gamma=\frac{1}{||w^*||}= {(\sum\limits_{i \in support \quad vector}\alph^*_i)}^{1/2}$ 。