[读书笔记] R语言实战 （十三） 广义线性模型

广义线性模型扩展了线性模型的框架，它包含了非正态的因变量分析

广义线性模型拟合形式：

$$g(\mu_\lambda) = \beta_0 + \sum_{j=1}^m\beta_jX_j$$

$g(\mu_\lambda)为连接函数$. 假设响应变量服从指数分布族中某个分布(不仅仅是正态分布)，极大扩展了标准线性模型，模型参数估计的推导依据是极大似然估计，而非最小二乘法.

可以放松Y为正态分布的假设，改为Y服从指数分布族中的一种分布即可

glm()函数：glm(formula,family=family(link=function), data = )

Logistic regression：响应变量为二值(0,1), 模型假设Y服从二项分布，线性模型拟合形式：

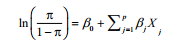
可用以下代码拟合Logistic回归：glm(Y~X1+X2+X3, family = binomial(link='logit',data=mydata)

#通过婚外情数据来预测婚外情情况
#每个参与者身上有9个变量：性别，年龄，婚龄，是否有小孩，宗教信仰程度，
#学历，职业，婚姻自我评分
library(AER)
data(Affairs,package = 'AER')
#查看描述性统计信息
summary(Affairs)
#将affairs转化Wie二值因子ynaaffair
Affairs$ynaffair[Affairs$affairs > 0] <-1
Affairs$ynaffair[Affairs$affairs == 0] <-0
Affairs$ynaaffair <- factor(Affairs$ynaffair,levels=c(0,1),labels=c("NO","Yes"))
table(Affairs$ynaffair)
#因子化之后的值可以作为Logistic回归的结果变量
fit.full <- glm(ynaffair~gender+age+yearsmarried+children+religiousness+education+occupation+rating,data=Affairs,family=binomial())
#描述模型
summary(fit.full)
#由P值得出性别，孩子，学历，职业对方程的贡献不显著，去除这些变量重新拟合
fit.reduced <- glm(ynaffair~age+yearsmarried+religiousness+rating,data=Affairs,family=binomial())
summary(fit.reduced)
#由结果可以看出这次个每个回归系数都很显著
#由于两个模型嵌套，可以使用anova()对他们进行比较
#卡方值p=0.21，表明四个预测变量的新模型与九个预测变量的模拟拟合程度一样好
anova(fit.reduced,fit.full,test='Chisq')
#解释模型系数：对数优势
coef(fit.reduced)
#指数优势
exp(coef(fit.reduced))
#评价预测变量对结果概率的影响
#婚姻评分对婚外情概率的影响
#创建虚拟数据集，年龄，婚龄，宗教信仰均为均值，婚姻评分为1-5
testdata <- data.frame(rating=c(1,2,3,4,5),age=mean(Affairs$age),yearsmarried=mean(Affairs$yearsmarried),religiousness=mean(Affairs$religiousness))
testdata$prob = predict(fit.reduced,newdata = testdata,type="response")
testdata

Logistic 回归变种：

• 稳健Logistic regression: robust包中glmRob()函数可以拟合文件的广义线性模型，当拟合回归模型出现离群点的强影响点时，稳健logistic regression便可以派生用场.
• 多项布回归，若响应变量包含两个以上无序类比(已婚，寡居，离婚)，便可以使用mlogit包中的mlogit()函数拟合多项Logistic回归
• 序数Logistic回归，若响应变量是一组有序类别(好，中，差)，便可以使用rms()包中的mlogit()函数拟合多项logistic回归

Poisson regression：响应变量为计数型, 模型假设Y服从泊松分布, 线性模型拟合形式：

许多分析标准线性模型lm()连用的函数在glm()中都有对应的形式：

 

#使用robust包中的癫痫数据Breslow，来讨论癫痫数据对癫痫发病率的影响
library(robust)
data(breslow.dat,package = "robust")
names(breslow.dat)
#我们只关注，Trt治疗条件，Age:年龄，基础癫痫发病数Base, 响应变量为sumY随机化后八周内癫痫发病数
summary(breslow.dat[c(6,7,8,10)])
opar <- par(no.readonly = TRUE)
par(mfrow=c(1,2))
attach(breslow.dat)
#图中可以看到因变量的偏倚特性和可能的离群点
hist(sumY,breaks = 20,xlab = "Seizure count",main="Distribution of Seizures")
boxplot(sumY~Trt,xlab="Treatment",main="Group Comarisons")
par(opar)
#拟合泊松回归
fit <- glm(sumY~Base+Age+Trt,data=breslow.dat,family=poisson())
summary(fit)
#获取模型系数
coef(fit)
exp(coef(fit))

　　

泊松回归的的变种：

• 时间段变化泊松回归
• 零膨胀泊松回归：logisitic regression + poisson regression

模型拟合和回归诊断：

1. 初始响应变量的预测值和残差的图形

2. 检验模型是否过度离势