结对编程作业1
1.改进现有代码
1.博客链接
201521123015
201521123017
2.码云
-
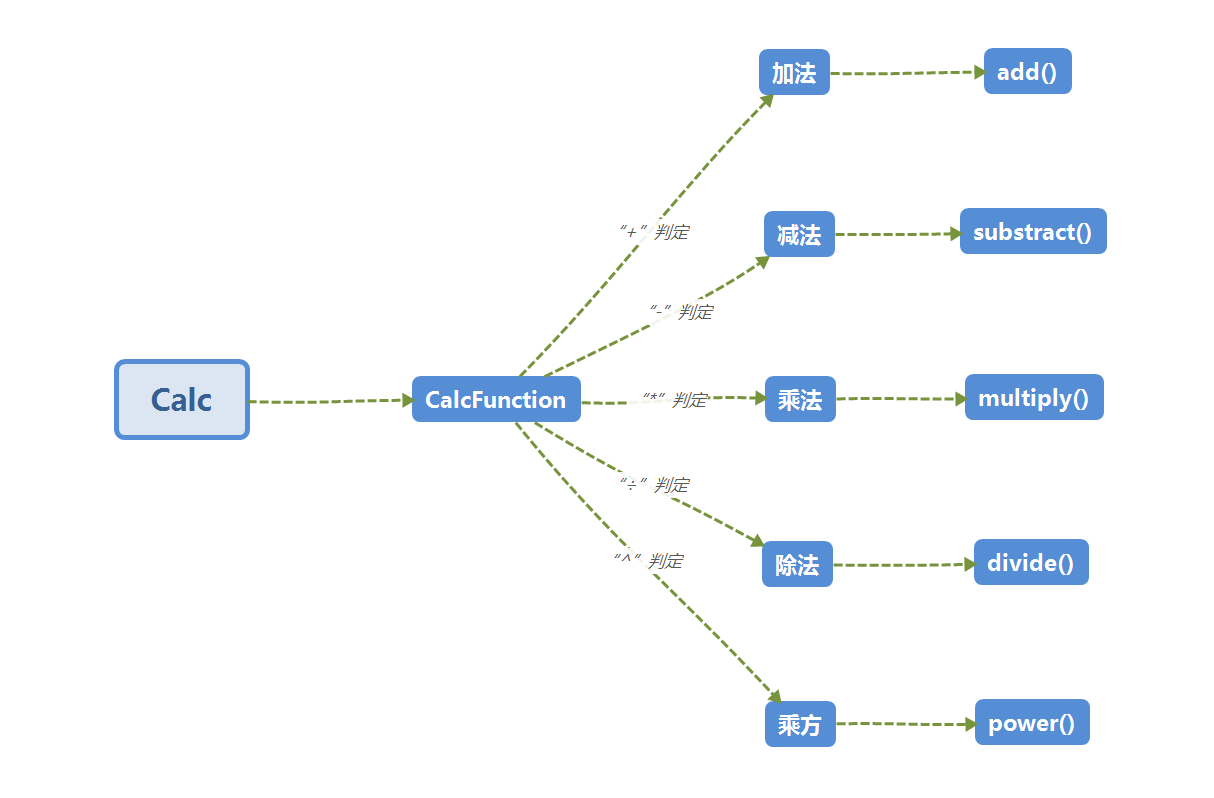
类图
-
JUnit单元测试
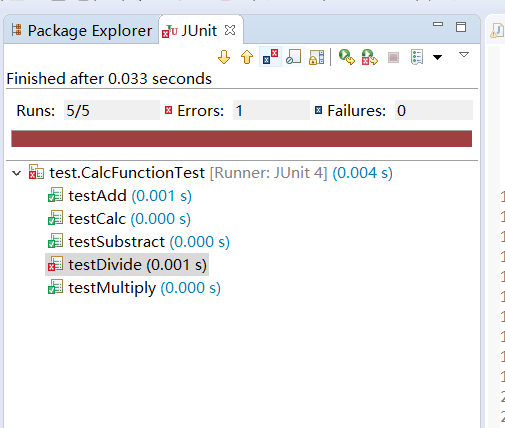
2.功能改进与扩展
- 代码
public void sqrt(String s)//根号
{
String[] str=s.split("\\#");
if(str[0].indexOf("/")>-1 )//分数
{
String[] str1=str[0].split("\\/");
if(Integer.parseInt(str1[1]) != 0 )//分母不为零
{
int a=Integer.parseInt(str1[0]);
int b=Integer.parseInt(str1[1]);
double a1=Math.sqrt(a);
double b1=Math.sqrt(b);
a=(int)a1;
b=(int)b1;
result=simplefraction(a,b);
}else{
throw new IllegalArgumentException("Divisor cannot be zero!");//除数为零时抛出异常
}
}
else{//整数
if( Integer.parseInt(str[0])<1000&&Integer.parseInt(str[1])<1000&&Integer.parseInt(str[0])>-1000&&Integer.parseInt(str[1])>-1000)
{
int c=Integer.parseInt(str[0]);
double c1=Math.sqrt(c);
c=(int)c1;
result = c+"";
}
else{
throw new IllegalArgumentException("overrun!");}//数值范围超出时抛出异常
}
}
if(s.indexOf("#")>-1){
int i=s.indexOf("#");
if(s.indexOf("#",i+1)==i+1){
throw new IllegalArgumentException("Input error! Don't like 1++1");//格式错误时抛出异常
}else{
sqrt(s);
}
}
- 运行截图
-
为了进一步提升原来四则运算小程序的功能，我加入了对数据进行求根的算法，然后通过JAVA中 Math.sqrt() 函数来实现这一功能。
-
需求分析阶段：现有的四则运算小程序拥有舒适的GUI界面，并且在界面能直接选择中文简体/中文繁体/英语三种语言，贴近用户需求，方便用户使用。其余的计时功能和保存错题数目也让次程序更有价值。然后我认为这个运算小程序在解决计算问题方面还略有不足，用户在使用程序时只能选择加减乘除和加入括号，不能满足用户日益增长的需求，所以我加入了对数值进行求根号的功能，让这个程序能完成更复杂的任务，进一步完善程序功能。
-
设计分析阶段：首先sqrt() 方法可返回一个数的平方根，通过调用Math.sqrt(x)函数可以计算一个数的任意次根，值得注意的是参数x是必需的，而且它必须是大于等于 0 的数。如果 x 小于 0，则返回 NaN。如果x是正无穷大，那么结果为正无穷大。而要实现一个sqrt函数，我们有几种方法，其中二分法是比较简单且中规中矩的。首先让我们确定一个范围[begin, end]，这个范围的中间数mid，看mid的平方是否等于x，如果相等，则返回mid，如果不等则缩小[begin,end]的范围，为原来的一半。这里的初始范围可以是[1, x]，也可以是更精确一些的[1, (x/2) + 1]。（因 (x/2) + 1 的平方等于 x+1+(x^2/4)，它一定大于x，所以，x的平方根一定在[1, (x/2) + 1]范围内）。但是这么做性能不高，牛顿迭代法是更好的选择。我们第一步就是构建曲线，假设有一个数c，我们求它的平方根x，那么有一个等式，x^2 = c；挪到一边就是求 f = x^2 - c的根x。第二步带入公式Xn+1=Xn-F(X(n))/F’(X(n))。第三部在迭代的开始，我们可以取c，而迭代的结束，就是和我们预期的很接近。那通过这么一个算法，我们就能很好得实现了求根这一功能。
-
代码风格规范和代码设计规范
3.两人编程
-
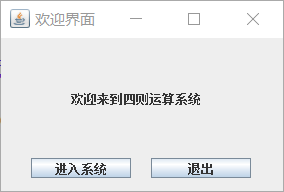
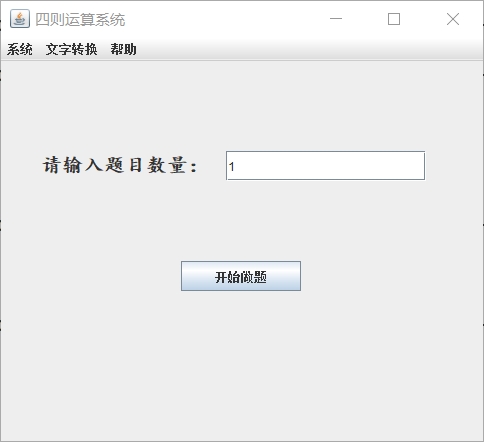
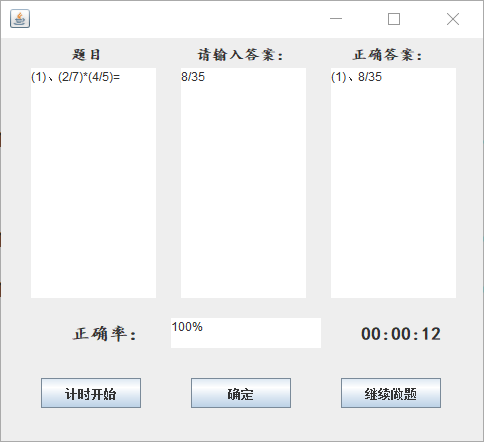
运行截图
- 四则运算优化
- 使用图形界面实现四则运算
-
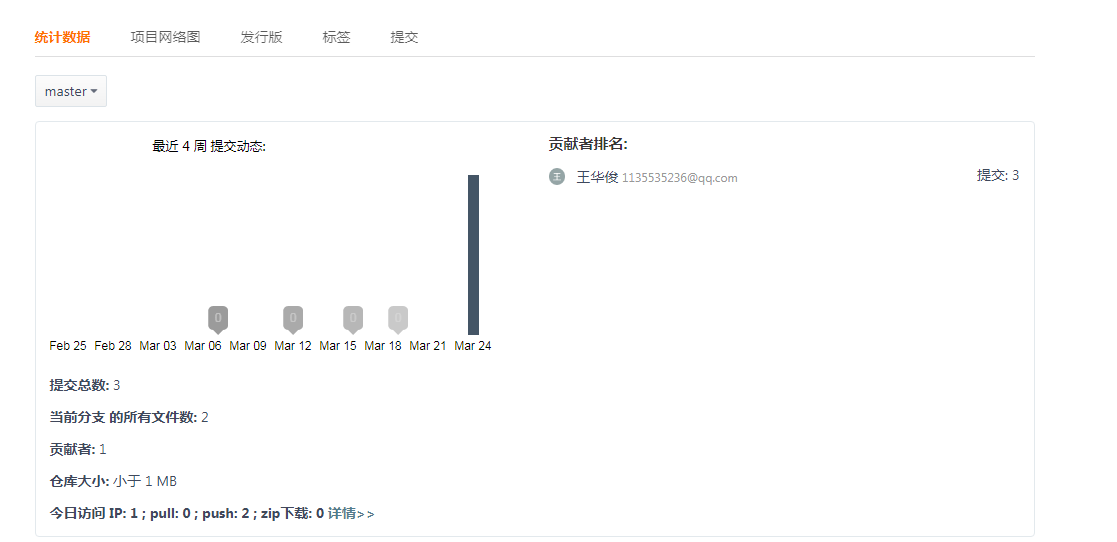
码云提交截图
- 四则运算优化
- 使用图形界面实现四则运算
-
结对编程照片
- 测评
| PSP2.1 | 个人开发流程 | 预估耗费时间（分钟） | 实际耗费时间（分钟） |
|---|---|---|---|
| Planning | 计划 | 10 | 15 |
| · Estimate | 明确需求和其他相关因素，估计每个阶段的时间成本 | 10 | 12 |
| Development | 开发 | 60 | 75 |
| · Analysis | 需求分析 (包括学习新技术) | 10 | 20 |
| · Design Spec | 生成设计文档 | 10 | 15 |
| · Design Review | 设计复审 | 6 | 8 |
| · Coding Standard | 代码规范 | 5 | 3 |
| · Design | 具体设计 | 8 | 9 |
| · Coding | 具体编码 | 40 | 45 |
| · Code Review | 代码复审 | 5 | 4 |
| · Test | 测试(自我测试，修改代码，提交修改) | 8 | 13 |
| Reporting | 报告 | 7 | 8 |
| . | 测试报告 | 3 | 2 |
| . | 计算工作量 | 1 | 1 |
| . | 并提出过程改进计划 | 3 | 3 |
