理解AUC
本文主要讨论了auc的实际意义,并给出了auc的常规计算方法及其证明
转载请注明出处:http://www.cnblogs.com/van19/p/5494908.html
1 ROC曲线和auc
从二分类说起,假设我们的样本全集里,所有样本的真实标签(label)为0或1,其中1表示正样本,0表示负样本,如果我们有一个分类模型,利用它对样本进行了标注,那边我们可以得到下面的划分
|
|
|
truth |
|
|
|
|
1 |
0 |
|
predictor |
1 |
TP |
FP |
|
0 |
FN |
TN |
|
TP(true positive):表示正确的肯定
TN( true negative):表示正确的否定
FP(false positive):表示错误的肯定
FN (false negative):表示错误的否定
简记:第一个字母表示最终结果true or false(正确或错误),第二个字母表示预测标签positive or negative(肯定或否定),从左往右读。例如FP,表示错误地肯定,即预测是1,而真实是0个样本个数。
由此,我们能得到TPR和FPR的定义
TPR(true positive rate):TPR = TP / T = TP / (TP + FN),表示预测为正的正确结果TP在所有正样本T中的占比,显然TPR越大,模型的预估能力更好。
FPR(false positive rate):FPR = FP / F = FP / (FP + TN) ,表示预测为正的错误结果FP在所有负样本F中的占比,显然FPR越大,模型的预估能力越差。
ROC曲线(receiver operating characteristic curve),由FPR为X轴坐标,TPR为Y轴坐标的曲线。下面介绍如何绘制ROC曲线
假设模型M对样本进行标注,当预测值大于某个阈值r时,我们用下面的函数来预测最后结果
$f(x)=\left\{\begin{matrix}1\ \ x\geqslant r\\0\ \ x<r\end{matrix}\right.$
然后,对于每一个r,模型对所有样本标注一遍,统计得到所有的TP和FP,就可以计算(fpr,tpr),对所有的点在ROC图上进行标注就可以得到ROC曲线,而本文的主题AUC就是指
ROC曲线下方的面积(Area under the Curve of ROC)。
下面我们来看一个实际的例子
下面表中有10个样本,其中5个正样本,5个负样本,即T=5,F=5。
|
score |
label |
|
0.15 |
1 |
|
0.12 |
1 |
|
0.11 |
0 |
|
0.1 |
0 |
|
0.04 |
0 |
|
0.04 |
1 |
|
0.03 |
1 |
|
0.02 |
0 |
|
0.012 |
1 |
|
0.01 |
0 |
我们让r从+∞逐渐较小至-∞,对每一个区间的r计算点(fpr,tpr),如下图
|
r |
fp |
tp |
fpr |
tpr |
|
(0.15,+∞) |
0 |
0 |
0 |
0 |
|
(0.12,0.15] |
0 |
1 |
0 |
0.2 |
|
(0.11,0.12] |
0 |
2 |
0 |
0.4 |
|
(0.1,0.11] |
1 |
2 |
0.2 |
0.4 |
|
(0.04,0.1] |
2 |
2 |
0.4 |
0.4 |
|
(0.03,0.04] |
3 |
3 |
0.6 |
0.6 |
|
(0.02,0.03] |
3 |
4 |
0.6 |
0.8 |
|
(0.012,0.02] |
4 |
4 |
0.8 |
0.8 |
|
(0.01,0.012] |
4 |
5 |
0.8 |
1 |
|
(-∞,0.01) |
5 |
5 |
1 |
1 |
由此描绘ROC曲线
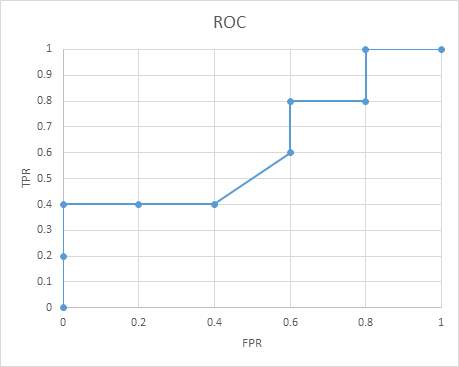
计算auc
auc即为ROC曲线下方的面积,按梯形法(连续两点构成的梯形)计算面积得到上面例子的auc为0.62。
2 AUC的实际意义
AUC表示,随机抽取一个正样本和一个负样本,分类器正确给出正样本的score高于负样本的概率。在所有标注样本中,正样本共T个,负样本共F个,如果随机抽一个正样本和负样本,共有T*F个pair,其中如果有s个pair的正负样本pair满足于正样本的score高于负样本(权重为1),v个pair正负样本score相同(权重为0.5),则auc就等于(s+0.5v)/(T*F)。本文的例子中,s=15,v=1,则auc=(15+1*0.5)/(5*5)=0.62,和梯形法计算面积的结果是一致。整体上对于某一个正负样本pair:<i,j>的权重Wij计算如下
$ W(i,j)=\left\{\begin{matrix}1\ \ s_i>s_j\\0.5\ s_i=s_j\\0\ \ s_i<s_j\end{matrix}\right.$
si和sj分别表示正样本i和负样本j的score。
下面我们对这个进行证明
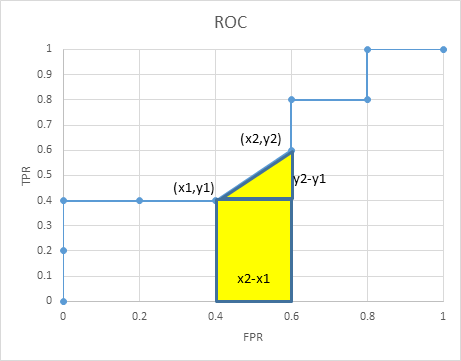
我们用梯形法,求摸一个梯形的面积时,如上图
图中黄色填充区域的面积是
$ S=(x_2-x_1)*(y_2+y_1)/2=(x_2-x_1)*y_1+0.5*(x_2-x_1)*(y_2-y_1) $
对S的分子分母同时乘以T*F,由于x*F=FP,y*T=TP,所以有
$ S=\frac{(FP_2-FP_1)*TP_1+0.5*(FP_2-FP_1)*(TP_2-TP_1)}{T*F}=\frac{\Delta FP*TP_1+0.5*\Delta FP*\Delta TP}{T*F} $
其中ΔFP=FP2-FP1>=0,表示随着r降低,本次计算roc点时新增的负样本数目;ΔTP=TP2-TP1>=0,表示随着r的降低,本次计算roc点时新增的正样本数目。
由上式可以看出,分母T*F表示所有正负样本的pair总数。
分子第一部分ΔFP*TP1表示新增正负样本pair数目,因为前一个的正样本数TP1和本次新增的负样本数ΔFP组成的pair都满足正样本的score高于负样本,这部分pair权重为1
分子第二部分ΔFP*ΔTP表示此次新增的同score的正负样本pair数目,这部分权重为0.5。
由此可知每一个梯形面积都表示此时正负样本pair满足正样本score大于等于负样本的加权计数值占全体正负样本pair的占比。从S0累计到最后一个Sn整体表示样本整体满足条件的正负样本的占比,此时等于AUC的面积计算值。
3 AUC的计算方法
到此为止,我们给出了计算auc的两种方法
1根据定义,由梯形法计算ROC曲线下的面积,求auc
2遍历全部样本,对正负pair的数目计数,求auc
在单机上,这两种算法的复杂度比较高,我们对方法2稍作改进,得到方法3
3我们可以将所有样本按升序排好后,通过样本的序号(或者说排序位置,从1开始)rank来计算,我们先给出公式
AUC=((所有的正样本rank相加)-T*(T+1)/2)/(T*F)
对相等score的样本,需要赋予相同的rank,即把所有这些score相等的样本的rank和取平均。
本文的例子(表1),按升序排好后如下表
|
rank |
score |
label |
|
1 |
0.01 |
0 |
|
2 |
0.012 |
1 |
|
3 |
0.02 |
0 |
|
4 |
0.03 |
1 |
|
5 |
0.04 |
0 |
|
6 |
0.04 |
1 |
|
7 |
0.1 |
0 |
|
8 |
0.11 |
0 |
|
9 |
0.12 |
1 |
|
10 |
0.15 |
1 |
所有的正样本rank相加=10+9+(5+6)/2+4+2=30.5,注意5和6由于score相同,需要均分rank和。
auc=(30.5-5*6/2)/(5*5)=0.62
下面我们证明一下这个计算公式和方法2计算是一致的
首先是分母部分,T*F表示所有正负样本pair数,对于分子部分
设每个正样本i的rank值为Ri,其score为si,
-
若Ri的score唯一,表示si大于Ri-1个样本,样本i和这Ri-1个样本组成的pair权值为1,所有此类正样本的rank之和表示和之前的所有Ri个样本组成的pair数(包括和自己的pair以及之前的正样本pair也算在内)
-
如Ri的score不唯一,不妨设此时有p个正样本和q个负样本score和i相同,那么此时有p*q个pair权值为0.5。
假设这连续p+q个样本中的第一个rank为t,则第p+q个样本的rank为t+p+q-1,根据方法3所述,这p+q个样本的rank值用平均rank来代替,为(t+t+p+q-1)/2,则p个正样本的ranker和为(t+t+p+q-1)*p*0.5=p*(t+t+p-1)/2+0.5*p*q。
我们看到第二项就是p*q个正负样本pair的加权和,而第一项是rank从r,r+1,…,r+p-1这p个正样本的rank和,它表示这p个正样本和r前面的样本组成的pair数(这p个样本和自己的pair和之前的正样本pair也算在内)。
从1和2分析看,所有正样本rank和会把正样本自己(共T个pair)和自己之前的所有正样本组成的pair(共T*(T-1)/2个pair)都计算一遍,并且权重为1,因此最后要去掉这个计数,这个计数就是T*(T+1)/2个pair,因此方法3的公式的分子算出来是正确正负样本pair的加权和。
4 总结
auc的意义
1 auc只反应模型对正负样本排序能力强弱,对score的大小和精度没有要求
2 auc越高模型的排序能力越强,理论上,当模型把所有正样本排在负样本之前时,auc为1.0,是理论最大值。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号