图的建立、广度优先遍历和深度优先遍历
图的建立、广度优先遍历和深度优先遍历
图分为有向图和无向图,再根据是否有权重又可以分为有权重图和无权重图。图常用的表示方式有邻接矩阵和邻接表。这里我们处理的图是有向、无权重图,采用的表示方式是邻接表。
图的数据保存在文件中,比如:
a 1 b
b 2 c e
c 1 f
d 2 c f
e 1 a
f 0
其中,第一个元素表示图中节点的名字,第二元素表示其可以直接到达的节点个数,后面紧跟着直接可以达到的节点。
我们采用的表示方式是邻接表,邻接表首先针对图中的节点定义一个数组,用来记录每个节点,数组中的每个节点元素后面跟着一个链表,在该链表中记录着其可以直接到达的节点。
节点的定义有以下几个部分:节点的名字,指向下一个节点的指针,是否被访问的标示符。
节点名字保存原始的字符串,这样在表示节点时,直接用字符串表示即可。也可以建立字符串到数字的映射以及数字到字符串的映射,即字符串和数字之间的双向映射,这里我们没有利用数字指代字符串来表示节点,而是直接使用的字符串。
表示图中节点是否被访问的标示符,我们将其放在节点中,也可以另外建立一个节点是否被访问的数组,如果我们放在节点中,那么链表中的节点也含有该标示符,但是我们只关注邻接表数组中的标示符,链表中的标示符不考虑,不过这样造成了链表中的标示符闲置,浪费了空间,这样做仅仅是为了描述方便。
图的遍历需要对图中节点记录是否已经被访问了,因为图中有可能存在环,即便不会倒回去,也有可能造成循环访问,如果添加了访问标识符,可以避免循环访问的情况。树的遍历则不需要添加访问标识符,因为书中不存在环,不会导致循环访问,而且不管图的遍历还是树的遍历,都不存在倒回去的情形。
上述文件中描述的有向图为:
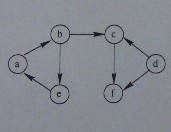
我们想根据给定的节点,输出其可以达到的其他节点。这是一个图遍历问题,可以采用广度优先遍历也可以采用深度优先遍历。
图的广度优先遍历类似于树的广度优先遍历,也是利用队列进行遍历,不同点在于图是用邻接矩阵或邻接表等表示,树是采用其特有的树结构来表示。不过树也可以用图的方式来表示,因为树本身就可以看作为图,图也可以用树来表示,图和树之间的差别就在于图比树多了一些边,树比图少了一些边。图的遍历和树的遍历差别在于图为了防止循环访问的情形,需要一个节点访问标识符,而树不需要。
图的深度优先遍历同样也类似于树的深度优先遍历。也是多了一个节点访问标示符。
广度优先遍历需要借助于队列来实现,因为广度优先遍历的逻辑符合队列先进先出的特点。而深度优先遍历需要借助于栈来实现,因为深度优先遍历的逻辑符合栈后进先出的特点。注意在深度优先遍历的过程中有两访问方式,第一种是在按照入栈的顺序访问,第二种是按照出栈的顺序访问。而队列的入队列和出队列顺序都是一样的。在实际实现的深度优先遍历中并不需要显式的栈,而是采用的函数递归调用,借助于函数递归调用中参数的隐式的栈。深度优先遍历虽然没有使用显式的栈,但是由于递归调用,还是采用了符合栈的逻辑特点。
下面我们将给出具体的程序实现,其中主要包含以下几个部分:
1.图节点的定义和生成
2.图的表示方式——邻接表
3.队列的定义和操作函数的实现
4.一些模块函数的封装
5.设置和查询节点的访问标识符
6.根据节点名字查找节点在邻接表数组中的索引
7.读取数据文件,并建立图对应的邻接表,并打印图
8.图的广度优先遍历
9.图的深度优先遍历
10.相关已建立结构的释放
11.测试
相关细节请查看代码和注释说明。
// 图的建立、广度遍历和深度遍历 #include <stdio.h> #include <stdlib.h> #include <string.h> #define M (100 + 1) // 定义节点结构体 typedef struct node_t { char* name; // 节点名 int visited; // 表示是否被访问,0表示未被访问,1表示被访问 struct node_t* next; // 指向下一个节点 } NODE; // 实现一个队列,用于后续操作 typedef struct queue_t { NODE** array; // array是个数组,其内部元素为NODE*型指针 int head; // 队列的头 int tail; // 队列的尾 int num; // 队列中元素的个数 int size; // 队列的大小 } QUEUE; // 内存分配函数 void* util_malloc(int size) { void* ptr = malloc(size); if (ptr == NULL) // 如果分配失败,则终止程序 { printf("Memory allocation error!\n"); exit(EXIT_FAILURE); } // 分配成功,则返回 return ptr; } // 字符串赋值函数 // 对strdup函数的封装,strdup函数直接进行字符串赋值,不用对被赋值指针分配空间 // 比strcpy用起来方便,但其不是标准库里面的函数 // 用strdup函数赋值的指针,在最后也是需要free掉的 char* util_strdup(char* src) { char* dst = strdup(src); if (dst == NULL) // 如果赋值失败,则终止程序 { printf ("Memroy allocation error!\n"); exit(EXIT_FAILURE); } // 赋值成功,返回 return dst; } // 对fopen函数封装 FILE* util_fopen(char* name, char* access) { FILE* fp = fopen(name, access); if (fp == NULL) // 如果打开文件失败,终止程序 { printf("Error opening file %s!\n", name); exit(EXIT_FAILURE); } // 打开成功,返回 return fp; } // 实现队列的操作 QUEUE* QUEUEinit(int size) { QUEUE* qp; qp = (QUEUE*)util_malloc(sizeof (QUEUE)); qp->size = size; qp->head = qp->tail = qp->num = 0; qp->array = (NODE**)util_malloc(size * sizeof (NODE*)); return qp; } // 入队列 int QUEUEenqueue(QUEUE* qp, NODE* data) { if (qp == NULL || qp->num >= qp->size) // qp未初始化或已满 { return 0; // 入队失败 } qp->array[qp->tail] = data; // 入队,tail一直指向最后一个元素的下一个位置 qp->tail = (qp->tail + 1) % (qp->size); // 循环队列 ++qp->num; return 1; } // 出队列 int QUEUEdequeue(QUEUE* qp, NODE** data_ptr) { if (qp == NULL || qp->num <= 0) // qp未初始化或队列内无元素 { return 0; } *data_ptr = qp->array[qp->head]; // 出队 qp->head = (qp->head + 1) % (qp->size); // 循环队列 --qp->num; return 1; } // 检测队列是否为空 int QUEUEempty(QUEUE* qp) { if (qp == NULL || qp->num <= 0) { return 1; } return 0; } // 销毁队列 void QUEUEdestroy(QUEUE* qp) { free(qp->array); free(qp); } // 以上是队列的有关操作实现 // 生成图中的节点 NODE* create_node() { NODE* q = NULL; q = (NODE*)util_malloc(sizeof (NODE)); q->name = NULL; q->visited = 0; q->next = NULL; return q; } // 设置访问标示visited void set_visited(char name[M], NODE* graph, int n) { int i = 0; for (i = 0; i < n; ++i) { if (strcmp(name, graph[i].name) == 0) { graph[i].visited = 1; return; } } } // 查找是否已经被访问,返回0表示未被访问,1表示被访问 int is_visited(char name[M], NODE* graph, int n) { int i = 0; for (i = 0; i < n; ++i) { if (strcmp(name, graph[i].name) == 0) { if (graph[i].visited == 1) // 被访问 { return 1; } else // 未被访问 { return 0; } } } return 0; } // 根据节点名,返回节点在邻接表中的索引 int find_index(char name[M], NODE* graph, int n) { int i = 0; for (i = 0; i < n; ++i) { if (strcmp(name, graph[i].name) == 0) { return i; } } return -1; } // 读取文件,建立邻接表 void read_file(NODE** graph, int* count, char* filename) { char name[M], adj[M]; int n = 0, i = 0, j = 0; FILE* fp = NULL; NODE* p1 = NULL, *p2 = NULL; *graph = (NODE*)util_malloc(M * sizeof (NODE)); *count = 0; fp = util_fopen(filename, "r"); // 打开文件 while (fscanf(fp, "%s %d", name, &n) != EOF) { (*graph)[i].name = util_strdup(name); (*graph)[i].visited = 0; (*graph)[i].next = NULL; p1 = &((*graph)[i]); for (j = 0; j < n; ++j) { fscanf(fp, "%s", adj); p2 = create_node(); p2->name = util_strdup(adj); //// 与文件中的节点顺序相反 //p2->next = p1->next; //p1->next = p2; //按照文件中的节点顺序 p1->next = p2; p1 = p2; } ++i; } *count = i; // 总共i个节点 fclose(fp); // 读取完毕 } void print_graph(NODE* graph, int n) { int i = 0; NODE* p = NULL; for (i = 0; i < n; ++i) { fprintf(stdout, "%s ", graph[i].name); p = graph[i].next; while (p != NULL) // not if (p != NULL) { fprintf(stdout, "%s ", p->name); p = p->next; } fprintf(stdout, "\n"); } } // 根据给定的节点查找到其能到达的其他节点 // 广度优先遍历 void func(char name[M], NODE* graph, int n) { NODE* p1 = NULL, *p2 = NULL; int index = 0, i = 0; QUEUE* q = NULL; // 将访问标识都置为0 for (i = 0; i < n; ++i) { graph[i].visited = 0; } q = QUEUEinit(100); // 初始化队列 index = find_index(name, graph, n); fprintf(stdout, "Reachable node:"); if (graph[index].next == NULL) { fprintf(stdout, "-\n"); return; } // 如果后面有节点 p1 = &(graph[index]); // 将该节点入队列 QUEUEenqueue(q, p1); // 该节点算作已经被访问了 graph[index].visited = 1; while (QUEUEempty(q) == 0) // 如果队列不为空 { // 出队列 QUEUEdequeue(q, &p1); p1 = p1->next; // ※这一步保证每次都不访问队列中的节点 while (p1 != NULL) { index = find_index(p1->name, graph, n); // 查找该节点的索引 if (graph[index].visited == 1) // 如果已经被访问过 { // 不做处理 ; } else // 如果还没有被访问 { // 输出该节点 fprintf(stdout, "%s ", p1->name); // 将该节点设置为被访问过 graph[index].visited = 1; // 将该节点入队列 QUEUEenqueue(q, &graph[index]); } p1 = p1->next; } } fprintf(stdout, "\n"); // 消毁队列 QUEUEdestroy(q); } // 深度优先遍历 void function2(char name[M], NODE* graph, int n, int* flag) { int index = 0; NODE* p1 = NULL, *p2 = NULL; index = find_index(name, graph, n); graph[index].visited = 1; // 一开始就被设置被访问,所以后面的设置visited可以忽略 p1 = graph[index].next; // 这一步很关键,不考虑邻接表数组中的元素,而是直接考虑数组中的元素后面链表中的元素 if (p1 == NULL) { return; } index = find_index(p1->name, graph, n); if (graph[index].visited == 1) { return; } while (p1 != NULL && graph[index].visited != 1) { *flag = 1; // 设置存有后续节点标识 fprintf(stdout, "%s ", p1->name); // 设置访问标示 index = find_index(p1->name, graph, n); // graph[index].visited = 1; // 这里可以被忽略,因为在函数开始出被设置了 p2 = &graph[index]; // 下一个深度的节点 function2(p2->name, graph, n, flag); p1 = p1->next; if (p1 != NULL) { index = find_index(p1->name, graph, n); // p1变了,index也要变 } else { break; } } } // 对深度优先遍历function2封装 void func2(char name[M], NODE* graph, int n) { int i = 0, flag = 0; for (i = 0; i < n; ++i) // 重置访问标示 { graph[i].visited = 0; } fprintf(stdout, "Reachable node-2:"); function2(name, graph, n, &flag); if (flag == 0) { fprintf(stdout, "-"); } fprintf(stdout, "\n"); } // 消毁图 void free_graph(NODE* graph, int n) { int i = 0; NODE* p1 = NULL, *p2 = NULL; if (graph == NULL) { return; } for (i = 0; i < n; ++i) { p1 = graph[i].next; free(graph[i].name); while (p1 != NULL) { p2 = p1->next; free(p1->name); free(p1); p1 = p2; } } free(graph); } int main(int argc, char* argv[]) { NODE* graph = NULL; char name[M]; int count = 0; if (argc != 2) { fprintf(stderr, "Missing parameters!\n"); exit(EXIT_FAILURE); } read_file(&graph, &count, "data.txt"); // 打印邻接表 // print_graph(graph, count); fprintf(stdout, ">Vertex:"); fscanf(stdin, "%s", name); while (strcmp(name, "end") != 0) { func(name, graph, count); func2(name, graph, count); fprintf(stdout, ">Vertex:"); fscanf(stdin, "%s", name); } free_graph(graph, count); return EXIT_SUCCESS; }
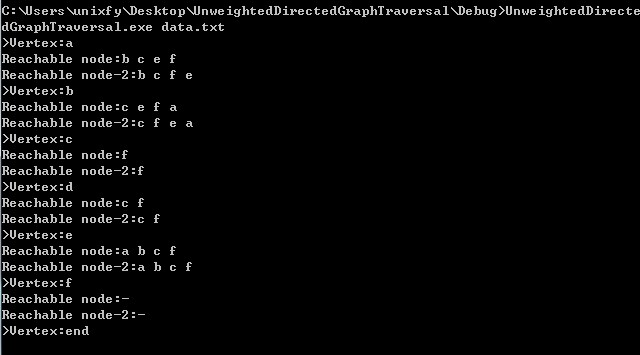
(完)
文档信息
·版权声明:自由转载-非商用-非衍生-保持署名 | Creative Commons BY-NC-ND 3.0
·博客地址:http://www.cnblogs.com/unixfy
·博客作者:unixfy
·作者邮箱:goonyangxiaofang(AT)163.com
·如果你觉得本博文的内容对你有价值,欢迎对博主 小额赞助支持


