DP--HDU 1003求数字串中的最大连续序列（含有DP过程详细分析）

题意如标题所示，求数字串的子序列中，和最大的那个子序列的和。测试数据规模为100000。

首先从DP的角度考虑

状态：i（数组下标）

状态转移方程：

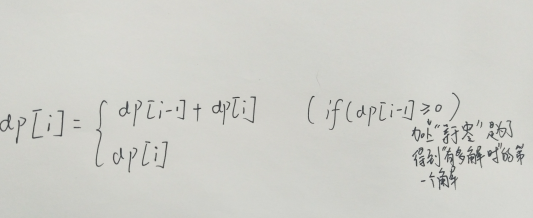 注：加上“等于零”是为了得到有多解时，的第一个解。（原谅我的字  -_-）

初始边界状态极其值：dp[0]。

最大连续序列和：定义一个max_sum=dp[0]，从前到后，根据状态转移方程不断更新

最大连续序列的起点与终点（这个我觉的非常容易写错）：定义begin与end初始为零，当状态转移方程满足上半部分时，end=i；满足下半部分时，令temp=i，直到后面有dp[i]>max_sum时，begin=i；

下面展示了一种错误情况，高亮部分为错误部分（好像看不到高亮，我又加了注释），很容易修改,不再给出ac代码，一个可以测试出其错误的样例是：

2
9 100 5 -105 -1 -1 10 10 10 1000
7 0 6 -1 1 -6 7 -5

另外，错误代码下面有一个ac代码，整个代码没有用数组实现了dp，非常值得一看。

错误代码：

#include <iostream>
using namespace std;

const int maxn=100000+10;  

int dp[maxn];

int main()  
{  
	freopen("in.txt","r",stdin);
	int c,n,begin,end;
	int count=0;
	scanf("%d",&c);
	for(int i=0;i<c;i++){
        scanf("%d",&n);
			for(int l=0;l<n;l++){
				scanf("%d",&dp[l]);
			}
			printf("Case %d:\n",++count);
			begin=end=0;
			int max_sum=dp[0];
			if(n>1)
			for(int l=1;l<n;l++){                //不能改为 l<=n 
				if( dp[l-1]>=0 ){
					dp[l]+=dp[l-1];
				}
				else{
					if(dp[l]>max_sum)   //错误部分
					begin=l;            //错误部分
				}
				if(max_sum<dp[l]){
					max_sum=dp[l];
					end=l;
				}
				max_sum=max_sum>dp[l]?max_sum:dp[l];
			}
			printf("%d %d %d\n",max_sum,begin+1,end+1);
        if(i!=(c-1))
        cout<<endl;
	}
	return 0; 
}  

#include<stdio.h>

int main(){
	freopen("in.txt","r",stdin); 
	int T,t,i,b,e,c,n,d,s,bb;
	scanf("%d",&T);
	for(t=1;t<=T;t++){
		scanf("%d",&n);
		bb=0;s=c=b=e=-999999;
		for(i=0;i<n;i++){
			scanf("%d",&d);
			if(c>=0) c+=d;else c=d,bb=i;
			if(c> s) b=bb,e=i,s=c;
	    }
	printf("Case %d:\n%d %d %d\n%s",t,s,b+1,e+1,t<T?"\n":"");
    }
    return 0;
}