kmeans理解
最近看到Andrew Ng的一篇论文,文中用到了Kmeans和DL结合的思想,突然发现自己对ML最基本的聚类算法都不清楚,于是着重的看了下Kmeans,并在网上找了程序跑了下。
kmeans是unsupervised learning最基本的一个聚类算法,我们可以用它来学习无标签的特征,其基本思想如下:
首先给出原始数据{x1,x2,...,xn},这些数据没有被标记的。
初始化k个随机数据u1,u2,...,uk,每一个ui都是一个聚类中心,k就是分为k类,这些xn和uk都是向量。
根据下面两个公式迭代就能求出最终所有的聚类中心u。
formula 1:
其中xi是第i个data,uj是第j(1~k)的聚类中心,这个公式的意思就是求出每一个data到k个聚类中心的距离,并求出最小距离,那么数据xi就可以归到这一类。
formula 2:
这个公式的目的是求出新的聚类中心,由于之前已经求出来每一个data到每一类的聚类中心uj,那么可以在每一类总求出其新的聚类中心(用这一类每一个data到中心的距离之和除以总的data),分别对k类同样的处理,这样我们就得到了k个新的聚类中心。
反复迭代公式一和公式二,知道聚类中心不怎么改变为止。
我们利用3维数据进行kmeans,代码如下:
run_means.m
1: %%用来kmeans聚类的一个小代码
2:
3: clear all;
4: close all;
5: clc;
6:
7: %第一类数据
8: mu1=[0 0 0]; %均值
9: S1=[0.3 0 0;0 0.35 0;0 0 0.3]; %协方差
10: data1=mvnrnd(mu1,S1,100); %产生高斯分布数据
11:
12: %%第二类数据
13: mu2=[1.25 1.25 1.25];
14: S2=[0.3 0 0;0 0.35 0;0 0 0.3];
15: data2=mvnrnd(mu2,S2,100);
16:
17: %第三个类数据
18: mu3=[-1.25 1.25 -1.25];
19: S3=[0.3 0 0;0 0.35 0;0 0 0.3];
20: data3=mvnrnd(mu3,S3,100);
21:
22: %显示数据
23: plot3(data1(:,1),data1(:,2),data1(:,3),'+');
24: hold on;
25: plot3(data2(:,1),data2(:,2),data2(:,3),'r+');
26: plot3(data3(:,1),data3(:,2),data3(:,3),'g+');
27: grid on;
28:
29: %三类数据合成一个不带标号的数据类
30: data=[data1;data2;data3]; %这里的data是不带标号的
31:
32: %k-means聚类
33: [u re]=KMeans(data,3); %最后产生带标号的数据,标号在所有数据的最后,意思就是数据再加一维度
34: [m n]=size(re);
35:
36: %最后显示聚类后的数据
37: figure;
38: hold on;
39: for i=1:m
40: if re(i,4)==1
41: plot3(re(i,1),re(i,2),re(i,3),'ro');
42: elseif re(i,4)==2
43: plot3(re(i,1),re(i,2),re(i,3),'go');
44: else
45: plot3(re(i,1),re(i,2),re(i,3),'bo');
46: end
47: end
48: grid on;
KMeans.m
1: %N是数据一共分多少类
2: %data是输入的不带分类标号的数据
3: %u是每一类的中心
4: %re是返回的带分类标号的数据
5: function [u re]=KMeans(data,N)
6: [m n]=size(data); %m是数据个数,n是数据维数
7: ma=zeros(n); %每一维最大的数
8: mi=zeros(n); %每一维最小的数
9: u=zeros(N,n); %随机初始化,最终迭代到每一类的中心位置
10: for i=1:n
11: ma(i)=max(data(:,i)); %每一维最大的数
12: mi(i)=min(data(:,i)); %每一维最小的数
13: for j=1:N
14: u(j,i)=ma(i)+(mi(i)-ma(i))*rand(); %随机初始化,不过还是在每一维[min max]中初始化好些
15: end
16: end
17:
18: while 1
19: pre_u=u; %上一次求得的中心位置
20: for i=1:N
21: tmp{i}=[]; % 公式一中的x(i)-uj,为公式一实现做准备
22: for j=1:m
23: tmp{i}=[tmp{i};data(j,:)-u(i,:)];
24: end
25: end
26:
27: quan=zeros(m,N);
28: for i=1:m %公式一的实现
29: c=[]; %c 是到每类的距离
30: for j=1:N
31: c=[c norm(tmp{j}(i,:))];
32: end
33: [junk index]=min(c);
34: quan(i,index)=norm(tmp{index}(i,:));
35: end
36:
37: for i=1:N %公式二的实现
38: for j=1:n
39: u(i,j)=sum(quan(:,i).*data(:,j))/sum(quan(:,i));
40: end
41: end
42:
43: if norm(pre_u-u)<0.1 %不断迭代直到位置不再变化
44: break;
45: end
46: end
47:
48: re=[];
49: for i=1:m
50: tmp=[];
51: for j=1:N
52: tmp=[tmp norm(data(i,:)-u(j,:))];
53: end
54: [junk index]=min(tmp);
55: re=[re;data(i,:) index];
56: end
57:
58: end
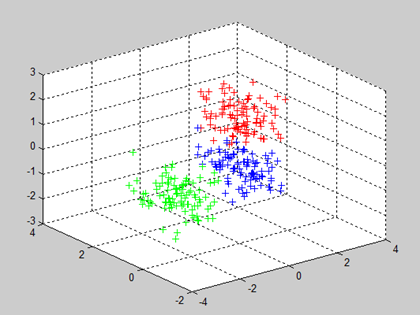
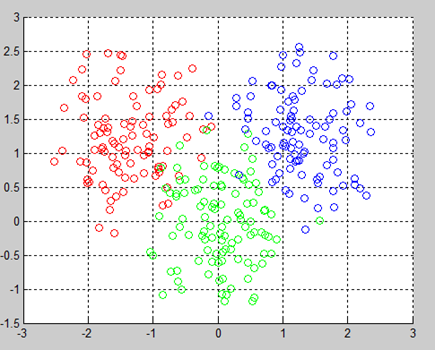
原始数据如下所示,分为三类:
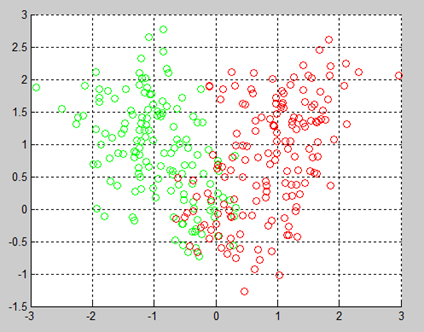
当k取2时,聚成2类:
当k取3时,聚成3类:


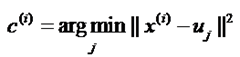
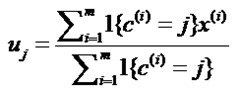


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 为什么说在企业级应用开发中,后端往往是效率杀手?
· 用 C# 插值字符串处理器写一个 sscanf
· Java 中堆内存和栈内存上的数据分布和特点
· 开发中对象命名的一点思考
· .NET Core内存结构体系(Windows环境)底层原理浅谈
· 为什么说在企业级应用开发中,后端往往是效率杀手?
· 本地部署DeepSeek后,没有好看的交互界面怎么行!
· 趁着过年的时候手搓了一个低代码框架
· 推荐一个DeepSeek 大模型的免费 API 项目!兼容OpenAI接口!
· 用 C# 插值字符串处理器写一个 sscanf