蓄水池抽样 - Reservoir Sampling
2012-08-10 17:08 coodoing 阅读(1056) 评论(0) 编辑 收藏 举报蓄水池抽样一般用于海量数据不知道总数只能遍历一次随机抽样问题。
第一部分:问题描述
问题起源于编程珠玑Column 12中的题目10,其描述如下:
How could you select one of n objects at random, where you see the objects sequentially but you do not know the value of n beforehand? For concreteness, how would you read a text file, and select and print one random line, when you don’t know the number of lines in advance?
问题1: 问题定义可以简化如下:在不知道文件总行数的情况下,如何从文件中随机的抽取一行?
首先想到的是我们做过类似的题目吗?当然,在知道文件行数的情况下,我们可以很容易的用C运行库的rand函数随机的获得一个行数,从而随机的取出一行,但是,当前的情况是不知道行数,这样如何求呢?我们需要一个概念来帮助我们做出猜想,来使得对每一行取出的概率相等,也即随机。这个概念即蓄水池抽样(Reservoir Sampling)。 有了这个概念,我们便有了这样一个解决方案:定义取出的行号为choice,第一次直接以第一行作为取出行 choice ,而后第二次以二分之一概率决定是否用第二行替换 choice ,第三次以三分之一的概率决定是否以第三行替换 choice ……,以此类推。可用伪代码描述如下:
i = 0
while more input lines
with probability 1.0/++i
choice = this input line
print choice
这种方法的巧妙之处在于成功的构造出了一种方式使得最后可以证明对每一行的取出概率都为1/n(其中n为当前扫描到的文件行数),换句话说对每一行取出的概率均相等,也即完成了随机的选取。
问题1转换为:证明当前任意一行被取出(为取出行choice)的概率为1/i,i为当前扫描到的行号,也即每一行取出的概率相等。我们用数学归纳法来证明。
证明:
1、当i=1时,当前只浏览了第一行,因此第一行为取出行的概率为1/1=1,符合直接取出的条件当i=k;
2、当i=2时,即浏览到第二行的时候,如果以1/2的概率替换掉choice情况的话,则概率为1/2 = 1/i;否则表明仍取出第一行为choice,这种情况的概率发生为:第一行为取出行choice的概率*第二行没有被取出的概率。1*1/2 = 1/2。
3、数学归纳法,假设前k行中每一行被取出的概率为1/k。我们需要证明的是,当i=k+1时:k+1行中每一行被取出的概率均相等,且为1/(k+1)。当扫描到第k+1行时,我们以1/(k+1)概率替换choice。易知第k+1行为choice的概率即为1/(k+1);对于第k行,其为choice的概率是: 第k行为取出行的概率 * 第k+1行没有被取出的概率。即
对于第k行的证明同样可应用到前k-1行,对于其中第m行其为choice的概率是 第m行为取出行的概率 * 第m+1行没有被取出的概率 * … *第k+1行没有被取出的概率,即
由此证得当i=k+1时,所有行的取出概率为1/(k+1)。证毕。
问题2:根据问题1,对其进行扩展。即如何从未知或者很大样本空间随机地取k个数?
类比下即可得到答案:即先把前k个数放入蓄水池,对第k+1,我们以k/(k+1)概率决定是否要把它换入蓄水池,换入时随机的选取一个作为替换项,这样一直做下去,对于任意的样本空间n,对每个数的选取概率都为k/n。也就是说对每个数选取概率相等。 伪代码如下:
Init : a reservoir with the size: k
for i= k+1 to N
M=random(1, i);
if( M < k)
SWAP the Mth value and ith value
end for
问题2转换为:证明对于任意样本号n(n>=k),每个样本作为取出样本的概率相等,即k/n。证明我们仍然使用数学归纳法。
证明:
1、当n=k时,由我们把前k个数放入蓄水池可知,在样本空间为n=k中随机选取k个数的概率为1,即每个元素被选中的概率为:k/n = k/k=1。
2、当n=k+1时,按照我们的规定,k+1这个元素被选中的概率是k/k+1,也即第 k+1 这个元素在蓄水池中出现的概率是k/k+1。
3、数学归纳法。设当前样本号为n,其每个取出样本概率均相等,即为k/n,我们要证明的是这种情况对于n+1也成立。即证明当以 k/(n+1) 的概率来选择第n+1个元素的时候,此时任一前n个元素出现在蓄水池的概率都为k/(n+1).
由于我们以k/(n+1)决定是否把第n+1个样本放入蓄水池,那么对于n+1样本空间而言,其出现在蓄水池中的概率就是k/(n+1)。对于前n个元素中的任意元素m(k+1<=m<=n),其最终被选中的概率: m被选中的概率*[m后面元素没有被选中+m后面的元素被选中*没被替换的概率],具体
m出现在蓄水池中的概率 * [(m+1被选中的概率*m没被m+1替换的概率 + m+1没被选中的概率)*(m+2被选中的概率*m没被m+2替换的概率 + m+2没被选中的概率)*…*(n+1被选中的概率*m没被n+1替换的概率 + n+1没被选中的概率)]。
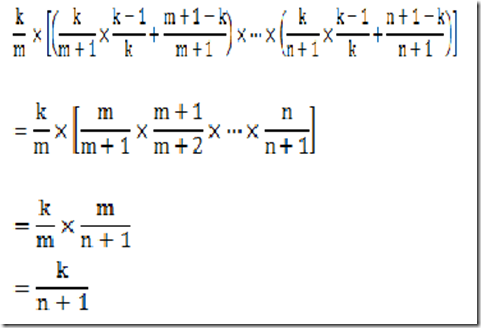
可见,对于n+1每个样本取出概率也相等,即为k/(n+1)。证毕。
蓄水池抽样问题是一类问题,在这里总结一下,并由衷的感叹这种方法之巧妙,不过对于这种思想产生的源头还是发觉不够,如果能够知道为什么以及怎么样想到这个解决方法的,定会更加有意义。
第二部分:应用
1. 给你一个长度为N的链表。N很大,但你不知道N有多大。你的任务是从这N个元素中随机取出k个元素。你只能遍历这个链表一次。你的算法必须保证取出的元素恰好有k个,且它们是完全随机的(出现概率均等)。
解答:
先选中前k个, 从第k+1个元素到最后一个元素为止, 以1/i (i=k+1, k+2,...,N) 的概率选中第i个元素,并且随机替换掉一个原先选中的元素, 这样遍历一次得到k个元素, 可以保证完全随机选取。这个算法叫做蓄水池抽样,在某门课上听到的,证明起来也不是很复杂。
可以参考编程珠玑问题12.10:如何从n个排序的对象中选择一个,但实现不知道n的大小?
解答:总是选择第一个对象,并使用1/2的概率选择第二个对象,使用1/3的概率选择第三个对象,以此类推。在过程结束时,每个对像被选中的概率都是1/n。伪码如下:
i = 0;
while( more objects)
{
with probability 1.0/i++
choice = this object
print choice
}
2、Given a random number generator which can generate the number in rang(1,5)uniformly, how can u use it to build a random number generator which can generate the number in range(1,7) uniformly?
解答:利用拒绝采样定理。
首先,将(1,5)之间的随机发生器使用两次,按照五进制进行使用,拼成一个(1,25)的随即发生器既:([gen][gen])5,每一[]为一个5进制上的位,换算为十进制为:x=gen*5+gen,在十进制上的范围为:6-30,进行一个简单的左移动,可换算成1-25范围上的值; 然后将(1,25)平均分配到7中情况上面,考虑21是7的倍数,因此可以每三个做一个映射(当然,也可以不管,直接截断7后面的数字,但是范围太小,效率不高),1-3--》1,4-6--》2,19-21--》7,此时就是等概率的,如果产生了22-25之间的数字,可以有两种方法决定结果:
(1)拒绝采样,重新再运算
(2)如果得到了22-25之间的数字,则此次的随即发生器结果,直接使用上一次得到的结果。这个方法有人证明过,是等概率的,算法Metropolis Algorithm。
3、将这个问题进一步抽象,已知random_m()随机数生成器的范围是[1, m] 求random_n()生成[1, n]范围的函数,m < n && n <= m *m。
一般解法如下,而具体分析可以参考文章:由rand7生成rand10以及随机数生成方法的讨论。
1: int random_n()
2: {
3: int val = 0;
4: int t; //t为n的最大倍数,且满足t<m*m
5: do
6: {
7: val = m * (random_m() - 1) + random_m();
8: }while(val > t);
9: return val;
10: }
参考资料:






