复旦大学2016--2017学年第一学期高等代数I期末考试情况分析
一、期末考试成绩班级前十名
宁盛臻(100)、朱民哲(92)、徐钰伦(86)、范凌虎(85)、沈伊南(84)、何陶然(84)、丁知愚(83)、焦思邈(83)、董瀚泽(82)、钱信(81)
二、总成绩计算方法
平时成绩根据交作业的次数决定,本学期共交作业13次,10次以上(包括10次)100分,少一次扣10分。
总成绩=平时成绩*20%+期中考试成绩*20%+期末考试成绩*60%
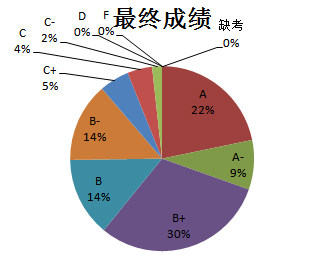
三、最终成绩及人数
| 最终成绩 | 人数 |
| A | 25 |
| A- | 10 |
| B+ | 35 |
| B | 16 |
| B- | 16 |
| C+ | 6 |
| C | 5 |
| C- | 2 |
| D | 0 |
| F | 0 |
| 缺考 | 0 |
| 合计 | 115 |
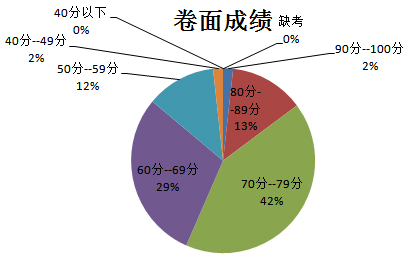
四、期末卷面成绩及人数
| 卷面成绩 | 人数 |
| 90分--100分 | 2 |
| 80分--89分 | 15 |
| 70分--79分 | 48 |
| 60分--69分 | 34 |
| 50分--59分 | 14 |
| 40分--49分 | 2 |
| 40分以下 | 0 |
| 缺考 | 0 |
| 合计 | 115 |
五、期末考试情况分析
本次期末试卷前面70分着重考察大家对基本概念的理解和计算基本功的掌握,但计算量不大并且计算过程比较舒适;后面30分的三道证明题着重考察大家对重要定理、方法和技巧的灵活应用(如利用降阶公式和摄动法求行列式的值,利用线性方程组的解证明矩阵秩的不等式等);试卷区分度较好,使得各个层次的同学都能得到发挥。从卷面成绩上看,86%的同学卷面成绩能上60分,57%的同学卷面成绩能上70分,这足以说明16级同学对高等代数I最基本的内容掌握地较好,完全达到了本学期高等代数I的教学目标。由于最后三道证明题都具有相当的难度(往年一般有一道证明题比较容易),所以这次期末考试上90分的同学只有2人,80--89分之间的同学只有15人。即便如此,班上还是有1位同学得到了满分;第六大题有12人完全做出;第七大题有5人完全做出,第八大题有8人完全做出,这也反映了16级还是有较多的拔尖同学,他们在证明难题方面具备了一定的功力。
六、对16级同学的寄语和期望
从本学期第四教学周开始,我还是在博客上推出了高代思考题的栏目,并且不定期地更新。不过同学们的反响并不积极,除了个别同学会通过微信提交解答给我浏览之外,其他同学或者没有做过,或者只在期中期末考试前匆忙做过,也没有与我进行交流和反馈(大概都忙着看很难的白皮书吧)。我认为在做思考题这方面,16级同学(特别是基础较好的同学)应该向14级的拔尖同学学习。要把三门基础课学好,除了认真和勤奋之外,还要有热情,不满足于基本的要求,也要敢于尝试和挑战一些难题,提升自己的思维论证能力。
期末考试第八大题并不是最难的一题(第七大题最难),所以很多同学都写了满满的一页(我改的很辛苦)。不过绝大部分同学的证明都是错的,其错误思想源于“能否从全空间的一组基中找到一部分基向量,使得它们是某个给定的真子空间的一组基”这一问题上。其实这个问题只要随便举几个二维平面或三维空间的例子,马上就知道是错的(高代教材上还有更强结论的习题:存在全空间的一组基,使得它们不包含在有限个给定的真子空间中),但在考试的时候,很多同学还是想当然地把这种错误思想写下来了。希望大家在今后学习高等代数的过程中,不仅要掌握代数工具,更要利用几何想象,但前提是要有正确的几何思维,多用低维空间或常见空间的例子去验证自己的想法,然后再严格地证明它们。
除了教16级同学高等代数课程之外,我还是你们的志德书院新生导师。还记得去年9月你们刚进入复旦时,应该都读过我写给你们的《数学之美与新生寄语》的文章吧!这个学期通过课堂课后的交流,以及志德书院的各项活动(新生导师下午茶和读书小组等),我逐渐地对16级同学有了更加深入的了解,也更加喜爱你们这个充满活力、积极向上的年级。希望你们在大学第一个学期逐步适应了复旦和数院的生活和学习之后,今后的路会越走越顺利,越走越好!我们这些基础课任课老师和新生导师们也会随时关注你们的成长,预祝大家在新的一年身体健康、学业进步!大家加油!



