Deep learning：二十五(Kmeans单层网络识别性能)

 

　　前言：

　　本文是用kmeans方法来分析单层网络的性能，主要是用在CIFAR-10图像识别数据库上。关于单层网络的性能可以参考前面的博文：Deep learning：二十(无监督特征学习中关于单层网络的分析)。当然了，本文依旧是参考论文An Analysis of Single-Layer Networks in Unsupervised Feature Learning, Adam Coates, Honglak Lee, and Andrew Y. Ng. In AISTATS 14, 2011.只是重点在分析4个算法中的kemans算法（因为作者只提供关于kmeans的demo，呵呵，当然了另一个原因是sparse autoencoder在前面的博文中也介绍很多了）本文的代码可以在Honglak Lee主页中下载：http://web.eecs.umich.edu/~honglak/

 

　　实验基础：

　　Kmeans相关：

　　Kmeans可以分为2个步骤，第一步是cluster assignment step，就是完成各个样本的聚类。第二步是move centroid，即重新选定类别中心点。Kmeans聚类不仅可以针对有比较明显类别的数据，还可以针对不具有明显类别的数据（即人眼看起来根本就没有区别），即使是没明显区分的数据用kmeans聚类时得到的结果也是可以进行解释的，因为有时候在某种原因下类别数是人定的。

　　既然kmeans是一种机器学习算法，那么它肯定也有一个目标函数需要优化，其目标函数如下所示：

 　　

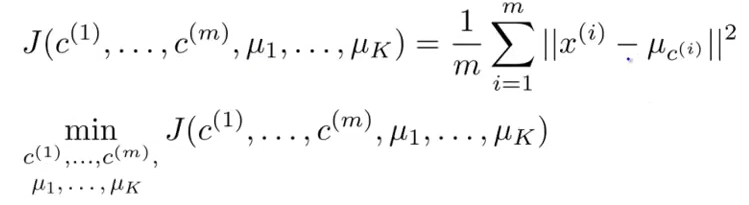
　　在kmeans初始化k个类别时，由于初始化具有随机性，如果选取的初始值点不同可能导致最后聚类的效果跟想象中的效果相差很远，这也就是kmeans的局部收敛问题。解决这个问题一般采用的方法是进行多次kmeans，然后计算每次kmeans的损失函数值，取损失函数最小对应的那个结果作为最终结果。

　　在kmeans中比较棘手的另一个问题是类别k的选择。因为有的数据集用不同的k来聚类都感觉比较合适，那么到底该用哪个k值呢？通常情况下的方法都是采用”elbow”的方法，即做一个图表，该图的横坐标为选取的类别个数k，纵坐标为kmeans的损失函数，通过观察该图找到曲线的转折点，一般这个图长得像人的手，而那个像人手肘对应的转折点就是我们最终要的类别数k，但这种方法也不一定合适，因为k的选择可以由人物确定，比如说我就是想把数据集分为10份（这种情况很常见，比如说对患者年龄进行分类），那么就让k等于10。

　　在本次试验中的kmeans算法是分为先求出每个样本的聚类类别，然后重新计算中心点这2个步骤。但是在求出每个样本的聚类类别是不是简单的计算那2个向量的欧式距离。而是通过内积实现的。我们要A矩阵中a样本和B矩阵中所有样本（此处用b表示）距离最小的一个求，即求min(a-b)^2，等价于求min(a^2+b^2-2*a*b)，等价于求max(a*b-0.5*a^2-0.5*b^2),假设a为输入数据中固定的一个， b为初始化中心点样本中的某一个，则固定的a和不同的b作比较时，此时a中的该数据可以忽略不计，只跟b有关。即原式等价于求max(a*b-0.5*b^2)。也就是runkmeans函数的核心思想。（这个程序一开始没看懂，后面慢慢推算总算弄明白了，应该是它这样通过矩阵操作进行kmeans距离的速度比较快吧！）

　　当通过聚类的方法得到了样本的k个中心以后就要开始提取样本的特征了，当然了这些样本特征的提取是根据每个样本到这k个类中心点的距离构成的，最简单的方法就是取最近邻，即取于这k个类别中心距离最近的那个类为类标签1，其它都为0，其计算公式如下：

 　　

　　因为那样计算就有很高的稀疏性（只有1个为1，其它 都为0），而如果需要放松条件则可以这样考虑：先计算出对应样本与k个类中心点的平均距离d，然后如果那些样本与类别中心点的距离大于d的话都设置为0，小于d的则用d与该距离之间的差来表示。这样基本能够保证一半以上的特征都变成0了，也是具有稀疏性的，且考虑了更多那些距类别中心距离比较近的值。此时的计算公式如下：

 　　

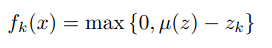
　　首先是关于CIFAR-10的数据库，到网站上http://www.cs.toronto.edu/~kriz/下载的CIFAR-10数据库解压后如下：

 　　

　　其中的每个data_batch都是10000x3072大小的，即有1w个样本图片，每个图片都是32*32且rgb三通道的，这里的每一行表示一个样本，与前面博文程序中的刚好相反。因为总共有5个data_batch，所以共有5w张训练图片。而测试数据test_batch则有1w张，是分别从10类中每类随机选取1000张。

　　关于均值化的一点总结：

　　给定多张图片构成的一个矩阵（其中每张图片看成是一个向量，多张图片就可以看做是一个矩阵了）。要对这个矩阵进行whitening操作，而在这之前是需要均值化的。在以前的实验中，有时候是对每一张图片内部做均值，也就是说均值是针对每张图片的所有维度，而有的时候是针对矩阵中图片的每一维做均值操作，那么是不是有矛盾呢？其实并不矛盾，主要是这两种均值化的目的不同。如果是算该均值的协方差矩阵，或者将一些训练样本输入到分类器训练前，则应该对每一维采取均值化操作（因为协方差均值是描述每个维度之间的关系）。如果是为了增强每张图片亮度的对比度，比如说在进行whitening操作前，则需要对图片的内部进行均值化（此时一般还会执行除以该图像内部的标准差操作）。

　　另外，一般输入svm分类器中的样本都是需要标准化过。

　　Matlab相关：

　　Matlab中function函数内部并不需要针对function有个end语句。

　　svd(),eig()：

　　其实按照道理这2者之间应该是完全不同的。相同之处是这2个函数的输入参数必须都是方阵。

　　cov:

　　cov(x)是求矩阵x的协方差矩阵。但对x是有要求，即x中每一行为一个样本，也就是说每一列为数据的一个维度值，不要求x均值化过。

　　var:

　　该函数是用来求方差的，求方差时如果是无偏估计则分母应该除以N-1,否则除以N即可。默认情况下分母是除以N-1的，即默认采用的是无偏估计。

　　b1 = var(a); % 按默认来求
　　b2 = var(a, 0); % 默认的公式（除以N-1）
　　c1 = var(a, 1); % 另外的公式（除以N）
　　d1 = var(a, 0, 1); % 对每列操作（除以N-1）
　　d2 = var(a, 0, 2); % 对每行操作（除以N-1）。

　　Im2col:

　　该函数是将一个大矩阵按照小矩阵取出来，并把取出的小矩阵展成列向量。比如说B = im2col(A,[m n],block_type):就是把A按照m*n的小矩阵块取出，取出后按照列的方式重新排列成向量,然后多个列向量组成一个矩阵。而参数block_type表示的是取出小矩形框的方式，有两种值可以取，分别为’distinct’和’sliding’。Distinct方式是指在取出的各小矩形在原矩阵中是没有重叠的，元素不足的补0。而sliding是每次移动一个元素，即各小矩形之间有元素重叠，但此时没有补0元素的说法。如果该参数不给出，则默认的为’sliding’模式。

　　random:

　　该函数和常见的rand,randi,randn不同，random可以产生各种不同的分布，其不同分布由参赛name决定，比如二项分布，泊松分布，指数分布等，其一般的调用形式为：   Y = random(name,A,B,C,[m,n,...])

　　rdivide：

　　在bsxfun(@rdivide,A,B)中，其中A是一个矩阵，B是一个行向量，则该函数的意思是将A中每个元素分别除以在B中对应列的值。

　　sum:

　　这里主要是想说进行多维矩阵的求sum操作，比如矩阵X为m*n*p维的，则sum(X,1)计算出的结果是1*n*p维的，而sum(x,2)后得到的尺寸是m*1*p维，sum(x,3) 后得到的尺寸是m*n*1维，也就是说，对哪一维求sum，则计算得到的结果后的那一维置1即可，其它可保持不变。

 

 

　　实验结果：

　　kemans学习到的类中心点图片显示如下：

　　

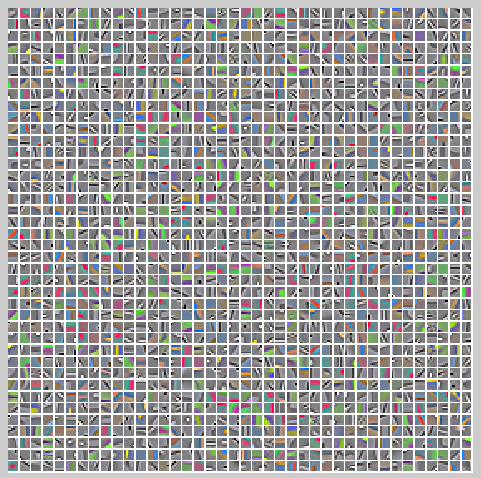
　　用kmeans方法对CIFAR-10训练图片的识别效果如下

　　Train accuracy 86.112000%

　　对测试图片识别的效果如下：

　　Test accuracy 77.350000%

 

　　实验主要部分代码：

kmeans_demo.m:

CIFAR_DIR='cifar-10-batches-mat/';

assert(strcmp(CIFAR_DIR, 'cifar-10-batches-mat/'), ...%strcmp相等时为1
       ['You need to modify kmeans_demo.m so that CIFAR_DIR points to ' ...
        'your cifar-10-batches-mat directory.  You can download this ' ...
        'data from:  http://www.cs.toronto.edu/~kriz/cifar-10-matlab.tar.gz']);

%% Configuration
addpath minFunc;
rfSize = 6;
numCentroids=1600;%类别总数
whitening=true;
numPatches = 400000;%40w张图片，不少啊！
CIFAR_DIM=[32 32 3];

%% Load CIFAR training data
fprintf('Loading training data...\n');
f1=load([CIFAR_DIR '/data_batch_1.mat']);
f2=load([CIFAR_DIR '/data_batch_2.mat']);
f3=load([CIFAR_DIR '/data_batch_3.mat']);
f4=load([CIFAR_DIR '/data_batch_4.mat']);
f5=load([CIFAR_DIR '/data_batch_5.mat']);

trainX = double([f1.data; f2.data; f3.data; f4.data; f5.data]);%50000*3072
trainY = double([f1.labels; f2.labels; f3.labels; f4.labels; f5.labels]) + 1; % add 1 to labels!,变成1到10
clear f1 f2 f3 f4 f5;%及时清除变量

% extract random patches
patches = zeros(numPatches, rfSize*rfSize*3);%400000*108
for i=1:numPatches
    i=1;
  if (mod(i,10000) == 0) fprintf('Extracting patch: %d / %d\n', i, numPatches); end
  
  r = random('unid', CIFAR_DIM(1) - rfSize + 1);%符合均一分布
  c = random('unid', CIFAR_DIM(2) - rfSize + 1);
  %使用mod(i-1,size(trainX,1))是因为对每个图片样本，提取出numPatches/size(trainX,1)个patch
  patch = reshape(trainX(mod(i-1,size(trainX,1))+1, :), CIFAR_DIM);%32*32*3
  patch = patch(r:r+rfSize-1,c:c+rfSize-1,:);%6*6*3
  patches(i,:) = patch(:)';%patches的每一行代表一个小样本
end

% normalize for contrast，亮度对比度均一化，减去每一行的均值然后除以该行的标准差（其实是标准差加10）
%bsxfun(@rdivide,A,B)表示A中每个元素除以B中对应行（或列）的值。
patches = bsxfun(@rdivide, bsxfun(@minus, patches, mean(patches,2)), sqrt(var(patches,[],2)+10));

% whiten
if (whitening)
  C = cov(patches);%计算patches的协方差矩阵
  M = mean(patches);
  [V,D] = eig(C);
  P = V * diag(sqrt(1./(diag(D) + 0.1))) * V';%P是ZCA Whitening矩阵
  %对数据矩阵白化前，应保证每一维的均值为0
  patches = bsxfun(@minus, patches, M) * P;%注意patches的行列表示的意义不同时，白化矩阵的位置也是不同的。
end

% run K-means
centroids = run_kmeans(patches, numCentroids, 50);%对样本数据patches进行聚类，聚类结果保存在centroids中
show_centroids(centroids, rfSize); drawnow;

% extract training features
if (whitening)
  trainXC = extract_features(trainX, centroids, rfSize, CIFAR_DIM, M,P);%M为均值向量，P为白化矩阵，CIFAR_DIM为patch的维数，rfSize为小patch的大小
else
  trainXC = extract_features(trainX, centroids, rfSize, CIFAR_DIM);
end

% standardize data，保证输入svm分类器中的数据都是标准化过了的
trainXC_mean = mean(trainXC);
trainXC_sd = sqrt(var(trainXC)+0.01);
trainXCs = bsxfun(@rdivide, bsxfun(@minus, trainXC, trainXC_mean), trainXC_sd);
trainXCs = [trainXCs, ones(size(trainXCs,1),1)];%每一个特征后面都添加了一个常量1

% train classifier using SVM
C = 100;
theta = train_svm(trainXCs, trainY, C);

[val,labels] = max(trainXCs*theta, [], 2);
fprintf('Train accuracy %f%%\n', 100 * (1 - sum(labels ~= trainY) / length(trainY)));

%%%%% TESTING %%%%%

%% Load CIFAR test data
fprintf('Loading test data...\n');
f1=load([CIFAR_DIR '/test_batch.mat']);
testX = double(f1.data);
testY = double(f1.labels) + 1;
clear f1;

% compute testing features and standardize
if (whitening)
  testXC = extract_features(testX, centroids, rfSize, CIFAR_DIM, M,P);
else
  testXC = extract_features(testX, centroids, rfSize, CIFAR_DIM);
end
testXCs = bsxfun(@rdivide, bsxfun(@minus, testXC, trainXC_mean), trainXC_sd);
testXCs = [testXCs, ones(size(testXCs,1),1)];

% test and print result
[val,labels] = max(testXCs*theta, [], 2);
fprintf('Test accuracy %f%%\n', 100 * (1 - sum(labels ~= testY) / length(testY)));

　　

run_kmeans.m:

function centroids = runkmeans(X, k, iterations)

  x2 = sum(X.^2,2);%每一个样本元素的平方和，x2这里指每个样本点与原点之间的欧式距离。
  centroids = randn(k,size(X,2))*0.1;%X(randsample(size(X,1), k), :); 程序中传进来的k为1600，即有1600个聚类类别
  BATCH_SIZE=1000;
  
  
  for itr = 1:iterations%iterations为kemans聚类迭代的次数
    fprintf('K-means iteration %d / %d\n', itr, iterations);
    
    c2 = 0.5*sum(centroids.^2,2);%c2表示类别中心点到原点之间的欧式距离

    summation = zeros(k, size(X,2));
    counts = zeros(k, 1);
    
    loss =0;
    
    for i=1:BATCH_SIZE:size(X,1) %X输入的参数为50000，所以该循环能够进行50次
      lastIndex=min(i+BATCH_SIZE-1, size(X,1));%lastIndex=1000,2000,3000,...
      m = lastIndex - i + 1;%m=1000,2000,3000,...
      %这种算法也是求每个样本的标签，因为求min(a-b)^2等价于求min(a^2+b^2-2*a*b)等价于求max(a*b-0.5*a^2-0.5*b^2),假设a为输入数据矩阵，而b为初始化中心点样本
      %则每次从a中取出一个数据与b中所有中心点作比较时，此时a中的该数据可以忽略不计，只跟b有关。即原式等价于求max(a*b-0.5*a^2)
      [val,labels] = max(bsxfun(@minus,centroids*X(i:lastIndex,:)',c2));%val为BATCH_SIZE大小的行向量（1000*1），labels为每个样本经过一次迭代后所属的类别标号
      loss = loss + sum(0.5*x2(i:lastIndex) - val');%求出loss没什么用
      
      S = sparse(1:m,labels,1,m,k,m); % labels as indicator matrix，最后一个参数为最大非0个数
      summation = summation + S'*X(i:lastIndex,:);%1600*108
      counts = counts + sum(S,1)';%1600*1的列向量，每个元素代表属于该类样本的个数
    end


    centroids = bsxfun(@rdivide, summation, counts);%步骤2，move centroids
    
    % just zap empty centroids so they don't introduce NaNs everywhere.
    badIndex = find(counts == 0);
    centroids(badIndex, :) = 0;%防止出现无穷大的情况
  end

 

extract_features.m:

function XC = extract_features(X, centroids, rfSize, CIFAR_DIM, M,P)
  assert(nargin == 4 || nargin == 6);
  whitening = (nargin == 6);
  numCentroids = size(centroids,1);%numCentroids中心点的个数
  
  % compute features for all training images
  XC = zeros(size(X,1), numCentroids*4);%为什么是4呢？因为后面是分为4个区域来pooling的
  for i=1:size(X,1)
    if (mod(i,1000) == 0) fprintf('Extracting features: %d / %d\n', i, size(X,1)); end
    
    % extract overlapping sub-patches into rows of 'patches'
    patches = [ im2col(reshape(X(i,1:1024),CIFAR_DIM(1:2)), [rfSize rfSize]) ;%类似于convolution一样取出小的patches,patches中每一行都对应原图中一个小图像块的rgb
                im2col(reshape(X(i,1025:2048),CIFAR_DIM(1:2)), [rfSize rfSize]) ;%因此patches中每一行也代表一个rgb样本，每一行108维，每一张大图片在patches中占27*27行
                im2col(reshape(X(i,2049:end),CIFAR_DIM(1:2)), [rfSize rfSize]) ]';

    % do preprocessing for each patch
    
    % normalize for contrast，whitening前对每一个样本内部做均值
    patches = bsxfun(@rdivide, bsxfun(@minus, patches, mean(patches,2)), sqrt(var(patches,[],2)+10));
    % whiten
    if (whitening)
      patches = bsxfun(@minus, patches, M) * P;
    end
    
    % compute 'triangle' activation function
    xx = sum(patches.^2, 2);
    cc = sum(centroids.^2, 2)';
    xc = patches * centroids';
    
    z = sqrt( bsxfun(@plus, cc, bsxfun(@minus, xx, 2*xc)) ); % distances = xx^2+cc^2-2*xx*cc;
    [v,inds] = min(z,[],2);%中间的那个中括号不能少，否则会认为是将z中元素同2比较，现在的2表示z中的第2维
    mu = mean(z, 2); % average distance to centroids for each patch
    patches = max(bsxfun(@minus, mu, z), 0);%patches中每一行保存的是：小样本与这1600个类别中心距离的平均值减掉与每个类别中心的距离，限定最小距离为0
    % patches is now the data matrix of activations for each patch
    
    % reshape to numCentroids-channel image
    prows = CIFAR_DIM(1)-rfSize+1;
    pcols = CIFAR_DIM(2)-rfSize+1;
    patches = reshape(patches, prows, pcols, numCentroids);
    
    % pool over quadrants
    halfr = round(prows/2);
    halfc = round(pcols/2);
    q1 = sum(sum(patches(1:halfr, 1:halfc, :), 1),2);%求区域内像素之和，是个列向量，1600*1
    q2 = sum(sum(patches(halfr+1:end, 1:halfc, :), 1),2);
    q3 = sum(sum(patches(1:halfr, halfc+1:end, :), 1),2);
    q4 = sum(sum(patches(halfr+1:end, halfc+1:end, :), 1),2);
    
    % concatenate into feature vector
    XC(i,:) = [q1(:);q2(:);q3(:);q4(:)]';%类似于pooling操作
  end

　　

train_svm.m:

function theta = train_svm(trainXC, trainY, C)
  
  numClasses = max(trainY);
  %w0 = zeros(size(trainXC,2)*(numClasses-1), 1);
  w0 = zeros(size(trainXC,2)*numClasses, 1);
  w = minFunc(@my_l2svmloss, w0, struct('MaxIter', 1000, 'MaxFunEvals', 1000), ...
              trainXC, trainY, numClasses, C);

  theta = reshape(w, size(trainXC,2), numClasses);
  
% 1-vs-all L2-svm loss function;  similar to LibLinear.
function [loss, g] = my_l2svmloss(w, X, y, K, C)
  [M,N] = size(X);
  theta = reshape(w, N,K);
  Y = bsxfun(@(y,ypos) 2*(y==ypos)-1, y, 1:K);

  margin = max(0, 1 - Y .* (X*theta));
  loss = (0.5 * sum(theta.^2)) + C*mean(margin.^2);
  loss = sum(loss);  
  g = theta - 2*C/M * (X' * (margin .* Y));
  g = g(:);

  %[v,i] = max(X*theta,[],2);
  %sum(i ~= y) / length(y)

 

 

　　参考资料：

     Deep learning：二十(无监督特征学习中关于单层网络的分析)

　　An Analysis of Single-Layer Networks in Unsupervised Feature Learning, Adam Coates, Honglak Lee, and Andrew Y. Ng. In AISTATS 14, 2011.

      http://www.cs.toronto.edu/~kriz/

　　http://ai.stanford.edu/~ang/papers.php