Deep learning:十九(RBM简单理解)
这篇博客主要用来简单介绍下RBM网络,因为deep learning中的一个重要网络结构DBN就可以由RBM网络叠加而成,所以对RBM的理解有利于我们对DBN算法以及deep learning算法的进一步理解。Deep learning是从06年开始火得,得益于大牛Hinton的文章,不过这位大牛的文章比较晦涩难懂,公式太多,对于我这种菜鸟级别来说读懂它的paper压力太大。纵观大部分介绍RBM的paper,都会提到能量函数。因此有必要先了解下能量函数的概念。参考网页http://202.197.191.225:8080/30/text/chapter06/6_2t24.htm关于能量函数的介绍:
一个事物有相应的稳态,如在一个碗内的小球会停留在碗底,即使受到扰动偏离了碗底,在扰动消失后,它会回到碗底。学过物理的人都知道,稳态是它势能最低的状态。因此稳态对应与某一种能量的最低状态。将这种概念引用到Hopfield网络中去,Hopfield构造了一种能量函数的定义。这是他所作的一大贡献。引进能量函数概念可以进一步加深对这一类动力系统性质的认识,可以把求稳态变成一个求极值与优化的问题,从而为Hopfield网络找到一个解优化问题的应用。
下面来看看RBM网络,其结构图如下所示:
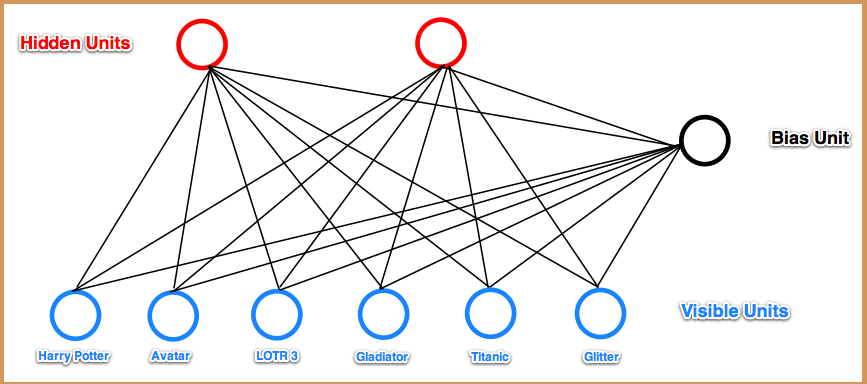
可以看到RBM网络共有2层,其中第一层称为可视层,一般来说是输入层,另一层是隐含层,也就是我们一般指的特征提取层。在一般的文章中,都把这2层的节点看做是二值的,也就是只能取0或1,当然了,RBM中节点是可以取实数值的,这里取二值只是为了更好的解释各种公式而已。在前面一系列的博文中可以知道,我们设计一个网络结构后,接下来就应该想方设法来求解网络中的参数值。而这又一般是通过最小化损失函数值来解得的,比如在autoencoder中是通过重构值和输入值之间的误差作为损失函数(当然了,一般都会对参数进行规制化的);在logistic回归中损失函数是与输出值和样本标注值的差有关。那么在RBM网络中,我们的损失函数的表达式是什么呢,损失函数的偏导函数又该怎么求呢?
在了解这个问题之前,我们还是先从能量函数出发。针对RBM模型而言,输入v向量和隐含层输出向量h之间的能量函数值为:
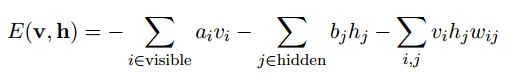
而这2者之间的联合概率为:
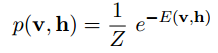
其中Z是归一化因子,其值为:
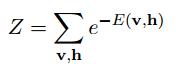
这里为了习惯,把输入v改成函数的自变量x,则关于x的概率分布函数为:

令一个中间变量F(x)为:
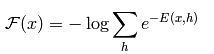
则x的概率分布可以重新写为:

这时候它的偏导函数取负后为:
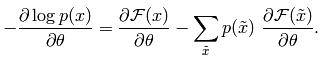
从上面能量函数的抽象介绍中可以看出,如果要使系统(这里即指RBM网络)达到稳定,则应该是系统的能量值最小,由上面的公式可知,要使能量E最小,应该使F(x)最小,也就是要使P(x)最大。因此此时的损失函数可以看做是-P(x),且求导时需要是加上负号的。
另外在图RBM中,可以很容易得到下面的概率值公式:
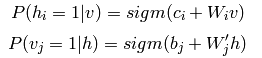
此时的F(v)为(也就是F(x)):
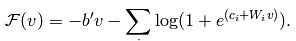
这个函数也被称做是自由能量函数。另外经过一些列的理论推导,可以求出损失函数的偏导函数公式为:
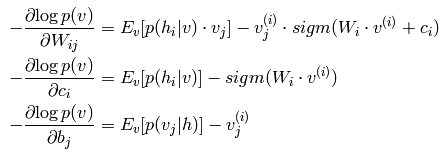
很明显,我们这里是吧-P(v)当成了损失函数了。另外,估计大家在看RBM相关文章时,一定会介绍Gibbs采样的知识,关于Gibbs内容可以简单参考上一篇博文:Deep learning:十八(关于随机采样)。那么为什么要用随机采用来得到数据呢,我们不是都有训练样本数据了么?其实这个问题我也一直没弄明白。在看过一些简单的RBM代码后,暂时只能这么理解:在上面文章最后的求偏导公式里,是两个数的减法,按照一般paper上所讲,这个被减数等于输入样本数据的自由能量函数期望值,而减数是模型产生样本数据的自由能量函数期望值。而这个模型样本数据就是利用Gibbs采样获得的,大概就是用原始的数据v输入到网络,计算输出h(1),然后又反推v(1),继续计算h(2),…,当最后反推出的v(k)和k比较接近时停止,这个时候的v(k)就是模型数据样本了。
也可以参考博文浅谈Deep Learning的基本思想和方法来理解:假设有一个二部图,每一层的节点之间没有链接,一层是可视层,即输入数据层(v),一层是隐藏层(h),如果假设所有的节点都是二值变量节点(只能取0或者1值),同时假设全概率分布p(v, h)满足Boltzmann 分布,我们称这个模型是Restrict Boltzmann Machine (RBM)。下面我们来看看为什么它是Deep Learning方法。首先,这个模型因为是二部图,所以在已知v的情况下,所有的隐藏节点之间是条件独立的,即p(h|v) =p(h1|v).....p(hn|v)。同理,在已知隐藏层h的情况下,所有的可视节点都是条件独立的,同时又由于所有的v和h满足Boltzmann 分布,因此,当输入v的时候,通过p(h|v) 可以得到隐藏层h,而得到隐藏层h之后,通过p(v|h) 又能得到可视层,通过调整参数,我们就是要使得从隐藏层得到的可视层v1与原来的可视层v如果一样,那么得到的隐藏层就是可视层另外一种表达,因此隐藏层可以作为可视层输入数据的特征,所以它就是一种Deep Learning方法。
参考资料:
http://202.197.191.225:8080/30/text/chapter06/6_2t24.htm
http://deeplearning.net/tutorial/rbm.html
http://edchedch.wordpress.com/2011/07/18/introduction-to-restricted-boltzmann-machines/



