Deep learning：十三(Softmax Regression)

 

　　在前面的logistic regression博文Deep learning：四(logistic regression练习) 中，我们知道logistic regression很适合做一些非线性方面的分类问题，不过它只适合处理二分类的问题，且在给出分类结果时还会给出结果的概率。那么如果需要用类似的方法（这里类似的方法指的是输出分类结果并且给出概率值）来处理多分类问题的话该怎么扩展呢？本次要讲的就是对logstic regression扩展的一种多分类器，softmax regression。参考的内容为网页：http://deeplearning.stanford.edu/wiki/index.php/Softmax_Regression

　　在Logistic regression中，所学习的系统的程为：

 　　

　　其对应的损失函数为：

 　　

　　可以看出，给定一个样本，就输出一个概率值，该概率值表示的含义是这个样本属于类别’1’的概率，因为总共才有2个类别，所以另一个类别的概率直接用1减掉刚刚的结果即可。如果现在的假设是多分类问题，比如说总共有k个类别。在softmax regression中这时候的系统的方程为：

 　　

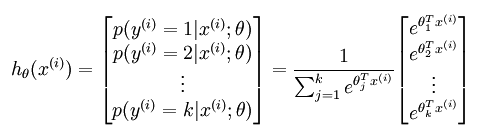
　　其中的参数sidta不再是列向量，而是一个矩阵，矩阵的每一行可以看做是一个类别所对应分类器的参数，总共有k行。所以矩阵sidta可以写成下面的形式：

 　　

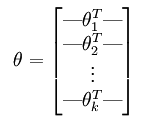
　　此时，系统损失函数的方程为：

 　　

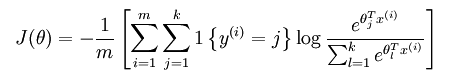
　　其中的1{.}是一个指示性函数，即当大括号中的值为真时，该函数的结果就为1，否则其结果就为0。

　　当然了，如果要用梯度下降法，牛顿法，或者L-BFGS法求得系统的参数的话，就必须求出损失函数的偏导函数，softmax regression中损失函数的偏导函数如下所示：

 　　

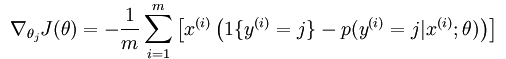
　　注意公式中的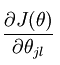是一个向量，表示的是针对第i个类别而求得的。所以上面的公式还只是一个类别的偏导公式，我们需要求出所有类别的偏导公式。表示的是损失函数对第j个类别的第l个参数的偏导。

　　比较有趣的时，softmax regression中对参数的最优化求解不只一个，每当求得一个优化参数时，如果将这个参数的每一项都减掉同一个数，其得到的损失函数值也是一样的。这说明这个参数不是唯一解。用数学公式证明过程如下所示：

 　　

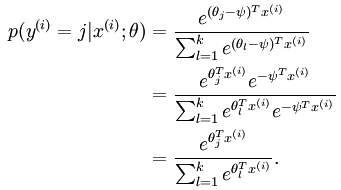
　　那这个到底是什么原因呢？从宏观上可以这么理解，因为此时的损失函数不是严格非凸的，也就是说在局部最小值点附近是一个”平坦”的，所以在这个参数附近的值都是一样的了。那么怎样避免这个问题呢？其实加入规则项就可以解决（比如说，用牛顿法求解时，hession矩阵如果没有加入规则项，就有可能不是可逆的从而导致了刚才的情况，如果加入了规则项后该hession矩阵就不会不可逆了），加入规则项后的损失函数表达式如下：

 　　

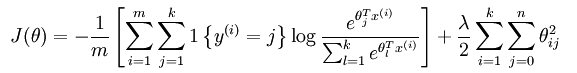
　　这个时候的偏导函数表达式如下所示：

 　　

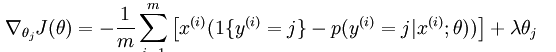
　　接下来剩下的问题就是用数学优化的方法来求解了，另外还可以从数学公式的角度去理解softmax regression是logistic regression的扩展。

　　网页教程中还介绍了softmax regression和k binary classifiers之间的区别和使用条件。总结就这么一个要点：如果所需的分类类别之间是严格相互排斥的，也就是两种类别不能同时被一个样本占有，这时候应该使用softmax regression。反正，如果所需分类的类别之间允许某些重叠，这时候就应该使用binary classifiers了。

 

　　参考资料：

     Deep learning：四(logistic regression练习)

     http://deeplearning.stanford.edu/wiki/index.php/Softmax_Regression