转：【拓扑排序详解】+【模板】

转自：http://www.cnblogs.com/skywang12345/p/3711489.html

拓扑排序介绍

拓扑排序(Topological Order)是指，将一个有向无环图(Directed Acyclic Graph简称DAG)进行排序进而得到一个有序的线性序列。

这样说，可能理解起来比较抽象。下面通过简单的例子进行说明！ 
例如，一个项目包括A、B、C、D四个子部分来完成，并且A依赖于B和D，C依赖于D。现在要制定一个计划，写出A、B、C、D的执行顺序。这时，就可以利用到拓扑排序，它就是用来确定事物发生的顺序的。

在拓扑排序中，如果存在一条从顶点A到顶点B的路径，那么在排序结果中B出现在A的后面。

拓扑排序的算法图解

拓扑排序算法的基本步骤：

1. 构造一个队列Q(queue) 和 拓扑排序的结果队列T(topological)； 
2. 把所有没有依赖顶点的节点放入Q； 
3. 当Q还有顶点的时候，执行下面步骤： 
3.1 从Q中取出一个顶点n(将n从Q中删掉)，并放入T(将n加入到结果集中)； 
3.2 对n每一个邻接点m(n是起点，m是终点)； 
3.2.1 去掉边<n,m>; 
3.2.2 如果m没有依赖顶点，则把m放入Q; 
注：顶点A没有依赖顶点，是指不存在以A为终点的边。

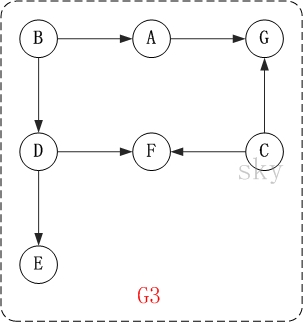
以上图为例，来对拓扑排序进行演示。

第1步：将B和C加入到排序结果中。 
    顶点B和顶点C都是没有依赖顶点，因此将C和C加入到结果集T中。假设ABCDEFG按顺序存储，因此先访问B，再访问C。访问B之后，去掉边<B,A>和<B,D>，并将A和D加入到队列Q中。同样的，去掉边<C,F>和<C,G>，并将F和G加入到Q中。 
    (01) 将B加入到排序结果中，然后去掉边<B,A>和<B,D>；此时，由于A和D没有依赖顶点，因此并将A和D加入到队列Q中。 
    (02) 将C加入到排序结果中，然后去掉边<C,F>和<C,G>；此时，由于F有依赖顶点D，G有依赖顶点A，因此不对F和G进行处理。 
第2步：将A,D依次加入到排序结果中。 
    第1步访问之后，A,D都是没有依赖顶点的，根据存储顺序，先访问A，然后访问D。访问之后，删除顶点A和顶点D的出边。 
第3步：将E,F,G依次加入到排序结果中。

因此访问顺序是：B -> C -> A -> D -> E -> F -> G

代码实现（邻接矩阵实现）

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
int indegree[100];
int n,m;
bool map[100][100];
int a[100];
int topu()
{
	queue<int> q;
    int cnt = 1;
    while(!q.empty())//清空队列 
        q.pop();
    for(int i = 1; i <= n ; i++)
        if(indegree[i] == 0)
            q.push(i);//将 没有依赖顶点的节点入队 
    int u;
    while(!q.empty())  //
	{
        u = q.front();
        a[cnt++] = u;//将上边选出的没有依赖顶点的节点加入到排序结果中 
        q.pop();//删除队顶元素  
        for(int i = 1; i <= n ; i++)
		{
            if(map[u][i])
			{
                indegree[i] --;//删去以u为顶点的边 
                if(indegree[i] == 0) //如果节点i的所有依赖顶点连接边都已经删去 
                    q.push(i);  //即变为无依赖顶点的节点   将其入队 
            }
        }
        if(cnt == n)//如果排序完成输出结果 
		{
            for(int i = 1 ; i <= n ; i++)
                printf(" %d",a[i]);
        }
    }
}
int main()
{
    int u,v;
    while(~scanf("%d%d",&n,&m))
	{
        memset(indegree,0,sizeof(indegree));
        memset(map,0,sizeof(map));
        for(int i = 0 ; i < m ; i++)
		{
            scanf("%d%d",&u,&v);
            if(!map[u][v])//考虑重边 
            {
            	indegree[v]++;//连接v的边的条数 
                map[u][v] = 1;//标记u v已经连接 
			}
        }
        topu();
    }
    return 0;
}