SFLA混合蛙跳算法
SFLA=SCE+PSO
SCE: shuffled complex evolution algorithm(Duan 1992) = CRS(controlled radom search Price 1978)+Competive evolution(Holland 1975)+shuffling
一、前言
1.1 SCE(混合复杂进化方法)的一些重要特征
- SCE算法背后的理念是将全局搜索作为自然进化的过程。人口被划分为几个社区(综合体),每个社区都被允许独立发展。经过定义的进化数量后,复合体被迫混合,新的群落通过洗牌过程形成。这一策略有助于通过共享每个社区独立获得的信息和属性来改进解决方案。
-
一个社区的每一个成员(complex)都是一个潜在的父母,有能力参与到一个繁殖过程中。
在每一个进化步骤中,只考虑复杂的子集(complex),即所谓的子复合体(subcomplexes)。
子复合体就像一对父母,除非有两个以上的成员。 -
为了确保进化过程具有竞争性,需要有更高的可能性,让更好的父母为下一代后代做出贡献。
三角形概率分布(triangular probability distribution)的使用确保了这一公平。 -
单纯型算法(Nelder和Mead 1965)是一种直接搜索方法,用来生成后代,例如进化子复合体(subcomplexes)。
这个策略使用包含在子复合体中的信息来指导改进方向的进化。 - 后代也会在可行的空间内随机地引入,以确保进化过程不会被困在贫穷地区,或错过解决方案空间的有希望的区域。
-
每一个新的后代都取代了目前最坏的子复合体(subcomplex),而不是整个种群中最糟糕的一点。
这种替换确保每个社区成员至少有一个机会在被丢弃或替换之前进行改进。
因此,社区中所包含的信息都没有被忽略。 -
SCE方法的设计是为了改进CRS方法(即全局采样和复杂演化)的最佳特征,通过整合竞争进化和复杂洗牌法的强大概念。
这两种技术都有助于确保样例中包含的信息能够有效地被充分利用。它们还确保信息集不会退化。
1.2 粒子群优化方法的一些重要特性
- 粒子群的优化是来自于对社会行为的模拟; 群体行为的同步行为被认为是鸟类努力维持自身与邻里之间的最佳距离的一种功能。
-
在PSO中,粒子(鸟)在飞行过程中经历了一段记忆的进化过程。
每个粒子都根据自己的飞行经验和同伴的飞行经验调整飞行状态。 -
一群粒子(鸟)是由位置和速度随机初始化的。
每个粒子都被看作是d维空间中的一个点。- 第i个粒子被表示为 XI=(xi1,xi2,…,Xi)
- 第i个粒子的最佳位置(给出最佳的健康值的位置)被记录并表示为PI=(pi1,pi2,…,piD)
-
粒子群中所有粒子中最好粒子的指数由Pg表示。
粒子i的位置变化速率(速度)表示为VI=(vi1,vi2,…,viD)
- 每个粒子的性能都是根据特定于问题的预定义的适应性函数来测量的。
- 粒子的速度和位置通过以下公式改变:
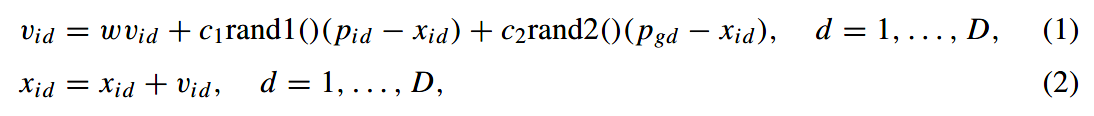
- c1和c2是两个正的常量,rand1()和rand2()是0到1的随机数,w是惯性权重。
- 公式1为:粒子的新速度是根据它先前的速度和从它自己最好的经验(位置)到当前位置的距离和团队的最佳经验。
- 然后粒子根据方程(2)飞向一个新的位置。
- 用惯性权重w来控制以前的历史速度对当前速度的影响。它指导了全局(范围广泛)和局部(附近)“飞行点”的探索能力之间的平衡。
- 更大的惯性权重w促进了全局探索(寻找新的区域),而较小的惯性权重则倾向于促进局部探索,从而对当前的搜索区域进行微调。
二、混合蛙跳算法——模因元启发式算法
2.1 虚拟的青蛙种群
每个个体都有一个相关的适应值来衡量个体的优秀。
在SFLA中,个体并不那么重要,而种群被看作是mems的宿主,也就是一个记忆载体。每个宿主都带有一个单一的meme(由memotype(s)组成。
正如前面所提到的,mems(模因)和memotypes(记忆体)分别与基因和染色体相似。
2.2 原理
想想一群青蛙在沼泽中跳跃,沼泽在离散的地方有很多石头,青蛙可以跳过这些石头来找到最大数量的可用食物。青蛙被允许互相交流,这样他们就可以利用别人的信息来改进他们的模因。在每个模因中,青蛙被其他青蛙的想法感染,因此他们经历了一个模因进化。模因进化提高了个体模因的质量,并提高了个体青蛙对目标的表现。
为了确保感染过程具有竞争性,需要有更好的模因(思想)的青蛙比那些思想贫乏的青蛙更能促进新思想的发展。用三角形概率分布选择青蛙为更好的想法提供了竞争优势。在进化过程中,青蛙可能会根据memeplex的信息或整个种群中最好的信息改变它们的模因。
2.3 详细介绍
SFLA是确定性和随机方法的结合。
确定性策略允许算法有效地使用响应表面信息来指导启发式搜索,就像在PSO中一样。随机元素确保了搜索模式的灵活性和健壮性。
搜索的开始是一群随机选择的青蛙,覆盖了整个沼泽。
人口被划分为几个平行的社区(memeplexe),它们被允许独立地发展,以在不同的方向上搜索空间。
在每一种记忆中,青蛙都被其他青蛙的想法所感染;因此他们经历了一场记忆进化。
记忆的进化提高了个体的模因的质量,并提高了个体蛙在目标上的表现。
为了确保感染过程具有竞争性,需要有更好的模因(想法)的青蛙比那些想法不佳的青蛙对新想法的发展做出更大的贡献。
在进化过程中,青蛙可能会利用从记忆中获得的信息或者整个种群中最好的信息来改变它们的迷因。
memotype(s)的增量变化对应于跳跃的步长,而新的模因与青蛙的新位置相对应。
当一只青蛙改进了它的位置后,它就被返回给了社区。
从位置变化中获得的信息可以立即得到进一步改进。
这种对新信息的瞬时可访问性将这种方法与GA分离开来,GA需要在新的见解可用之前对整个种群进行修改。
再一次,青蛙的视觉表现被用来做类比,但是,在思想的传播上,这个类比可以是发明者或研究人员改进一个概念或工程师迭代地推进一个设计。
算法运行完设定的模因进化步骤之后,模因组之间开始以混合的形式进行信息的交
换,这一混合过程与复合型混合演化算法类似。混合的过程也就是信息在不同模因组之
间的传递过程混合步骤通过每一个模因组中的青蛙与其它模因组中的青蛙进行交流,提
高了模因质量,此外,还保证了青蛙族群的进化过程朝着所有可能性进行,避免了算法
陷入局部最优解。混合过程之后,每一个模因组中的信息都被重置,局部搜索过程以及
混合过程会一直进行下去直到预设的收敛条件被满足。
三、steps
全局搜索
step 0 Initialize. 选择m和n。其中m是模因memeplexes的数量, n是 is 每个模因中青蛙的数量。在沼泽中总样本大小为F=mn。
step 1 生成一个虚拟人口。虚拟青蛙U(1), U(2), U(3), ..., U(F)
step 2 青蛙排序。对F型青蛙进行排序,以降低其性能值。储存在X队列中。记录下最好的青蛙的位置 PX =U(1) 。
step 3 分区青蛙into memeplexes。将数组X分割成 m个memeplexes Y1,Y2,…Ym,每一个都含有n个青蛙。
step 4 每个memplexes的内存演化。发展每个memeplex Yk,k = 1,…m 根据下面概述的青蛙跳跃算法。
step 5 重组模因。在每个memeplex中都有一个定义数量的memetic演化步骤,然后替换Y1…Ym 用X表示,X = {Yk,k = 1, .., m}。排序X以降低性能值。更新人口最佳青蛙的位置PX。
step 6 检查收敛。如果收敛条件满足,停止。否则,返回到步骤3。通常情况下,当至少一只青蛙携带着“最好的记忆模式”时,决定何时停止的决定是连续的时间循环。或者,可以定义一个最大的函数评估总数。
局部搜索:跳蛙算法
在全局搜索的第4步,每个memeplex的演化都独立地持续了N次。在memeplexes进化后,算法返回到对全局探索的重组。下面是对每个memeplex的局部搜索的详细信息。
step 0 设置im = 0,在这里我计算memeplex的数量,并将与memeplexes的总数m比较。
设置iN为= 0,iN用于计算进化步骤的数目,将与在每个memeplex中完成的步骤的最大数字N进行比较。
step 1 im=im+1
step 2 iN=iN+1
step 3 构造一个submemeplex。青蛙的目标是通过改进它们的模因来达到最优的想法。正如前面所提到的,他们可以从Yim或全球最好的青蛙中改编出最好的青蛙的想法。关于memeplex最好的选择,并不总是希望使用最好的青蛙,因为青蛙的倾向是集中在那只可能是局部最优的青蛙。因此,我们考虑了一个称为submemeplex的memeplex的子集。submemeplex选择策略是给具有较高的性能值的青蛙赋予更高的权重,而对具有较低性能值的青蛙的权重较小。权重是用三角形概率分布来分配的。
pj = 2(n + 1 − j)/n(n + 1), j = 1,...,n,这样,在一个memeplex中,具有最佳性能的青蛙将被选中为子memeplex的最高概率p1=2/(n+1),而最差性能的青蛙的概率最低,即pn=2/n(n+1)。
在这里,q不同的青蛙随机从每一个模内的n个青蛙中挑选出来,形成子memeplex阵列Z。子memeplex被排序,以便青蛙按降低的性能排列(iq = 1,…,q)。记录最好的(iq=1)青蛙的位置和最坏的(iq=q)青蛙的位置作为PB和PW的位置。submemeplex的概念如图1所示。
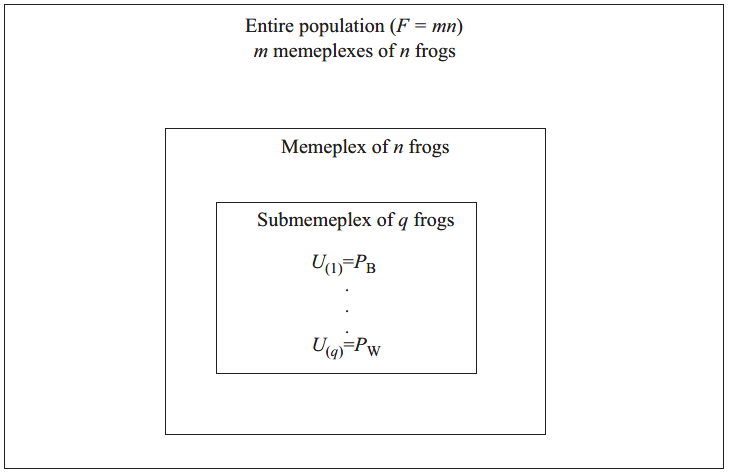
step 4 改善最差的青蛙的位置。子模因中表现最差的青蛙的步骤和新位置的计算方法:
步长 S = min{int[rand(PB − PW)], Smax} for a positive step,
= max{int[rand(PB − PW)], −Smax} for a negative step,
rand是一个随机数字在范围[0,1],而Smax是被感染后被青蛙允许通过的最大步长。注意,步骤大小的维度与决策变量的数量相等。然后计算新的位置:
U(q) = PW + S. (4)
如果U(q)在可行的空间Ω内,计算新的性能值f(q)。否则就到第5步。
如果新的f(q)比旧的f(q)更好。如果进化产生了一个好处,那么用新的U(q)替换旧的U(q),然后进入第7步。否则就到第5步。
图2显示了一个在submemeplex内的memetic进化(感染)的例子。

————————————————————————————————————————————————————————
每只青蛙都有一种模因meme,每一种模因都有五种记忆类型memotypes。例如,如果随机数是0.7,Smax的组件都是3,那么第一个memotype根据(1+min{int[rand(4-1)],3}=3)而改变,第三个memotype根据(5+max{int[rand(2-5)],-3}=3)来改变。
step5 如果第4步不能产生更好的结果,那么步骤和新位置就会被计算出来:
step size S = min{int[rand(PX − PW)], Smax} for a positive step,
= max{int[rand(PX − PW)], −Smax} for a negative step,
新位置用公式4计算。
如果U(q)在可行的空间Ω内,计算新的性能值f(q)。否则去第6步。
如果新的f(q)比旧的f(q)更好,也就是说,如果进化产生了一个好处,那么用新的U(q)替换旧的U(q),然后进入第7步。否则就到第6步。
step 6 审查制度。如果新位置是不可行的,或者没有比旧的位置好,那么有缺陷的模因的传播就会被随机生成一个新的青蛙r在一个可行的位置上,以取代新位置不适合进步的青蛙。
计算f(r)并设置U(q)=r和f(q)=f(r)。
step 7 升级memeplex。在submemeplex中最糟糕的青蛙的记忆改变之后,在Z的原始位置上替换为Yim。对Yim进行排序,以降低性能价值。
Step 8 If iN < N, 去第2步.
Step 9 If im < m, 去第1步. 否则,返回到全局搜索,以重新洗牌memeplexes。
局部搜索的步骤4和5在哲学上与PSO相似。一只青蛙的下降方向被识别出来,青蛙被移动到那个方向。然而,在这里,由于全局搜索也引入了洗牌操作,只有局部最小值被使用,而不是完整的最好种群(步骤4),除非没有改进(步骤5)。由于下降方向是隐式应用的,所以执行一个线性搜索而不是随机的步骤可能会更有效果,但是这里采用了更简单的方法。
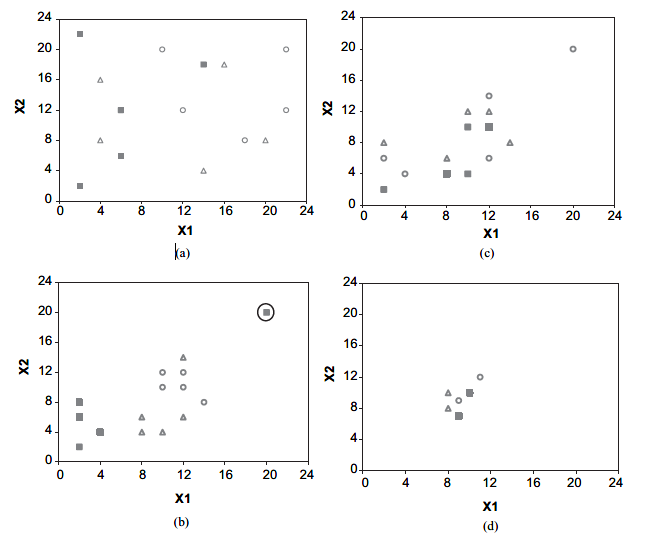
(a)虚拟青蛙的初始数量(在时间循环1的开始);
(b)独立进化的memeplexes(在时间循环1结束时);
(c)洗好的青蛙(在第二次循环的开始);
(d)独立进化的memeplexes(在时间循环2结束时)。
在图3(a)中,在沼泽的边界中随机选择了15个有不同模因的虚拟青蛙。它们分别被分成三组,分别用开放的三角形、全正方形和圆的圆圈表示。在每一种记忆中,表现不佳的青蛙都受到表现更好的青蛙的影响,并提高了它们的模因。
在一个时间循环中,允许有足够的N个memetic进化周期,以确保memeplex中的所有青蛙都有机会锻炼他们的想法。图3(b)显示了在一次循环结束时青蛙的位置。可以看出,每个memeplexes都是独立进化的,并导致了三个不同的本地搜索。
在进化过程中,有可能找到一只青蛙,它的想法不适合这个群体,它会触发审查制度,并产生一个新的虚拟青蛙,它有一组新的memes。
在图3(b)中,由满方格表示的memeplex中圈出的青蛙是一个审查的例子。
经过N个进化周期后,青蛙被重组以形成新的memeplexes,如图3(c)所示。新的memeplexes现在有了各种不同的想法。同样,memeplexes是独立于预先定义的几个周期的。图3(d)显示了在另一个时间循环结束时的3个memeplexes。所有的memeplexes(除了一些青蛙)都聚集在沼泽的最佳位置附近。最终,所有的青蛙都将被唯一的最优方案所感染,这代表了最佳的问题解决方案。
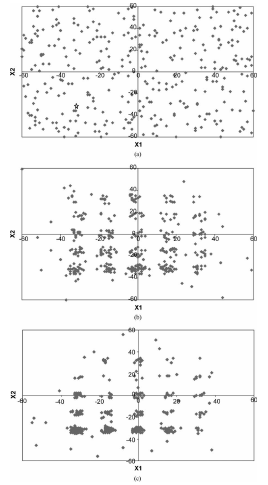
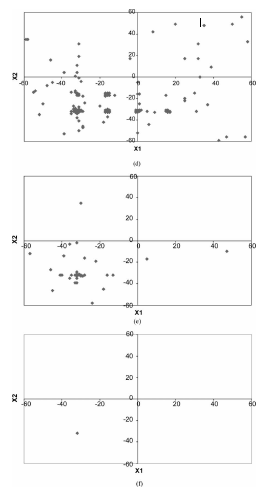
图4(a)-(f)显示了实际问题的算法的进展(DeJong的F5函数(稍后给出详细信息))。在搜索的最后,青蛙会趋向于同质化。图中青蛙的位置是根据它们的memes来定义的。在食物搜索的开始(时间循环1),青蛙被随机地分散在沼泽里(从-66到+66)。未知的最佳食物点(在图4(a)中显示的是一个开放的恒星,这是他们的最终目标。
随着时间的推移,青蛙已经被更好的想法感染,开始采用一些共同的想法并开始围绕局部最优(图4b)。随着进化和洗牌的继续,青蛙开始探索更多的新想法(时间循环6、10和15)(图4(c)-(e))。最后,在第20环,所有的青蛙都被相同的意识形态所感染,并聚集在最佳位置。
四、参数优化
与所有启发式一样,参数选择对SFLA的性能至关重要。
SFLA有五个参数: memeplexes的数量m,memeplex中青蛙的数量n, submemeplex中青蛙的数量q,在两个连续的洗牌之间的memeplex中N的进化或感染步骤,以及在进化过程中被允许的最大步长Smax。
在这个元启发式的发展过程中,没有明确的理论基础来决定参数值的选择。
根据经验,样本容量F(memeplexes的数字m乘以每个memeplex中青蛙的数量n)通常是最重要的参数。F的适当值与问题的复杂性有关。
找到全局(或接近全局)的最优的概率随着样本容量的增大而增加。然而,随着样例大小的增加,实现目标的函数评估的数量会增加,从而使计算变得更加繁重。此外,在选择m时,重要的是要确保n不是太小。
如果在每个模因中有太少的青蛙,则丢失了局部模因进化策略的优势。算法性能对q的响应是,当在子模因中选择的青蛙太少时,信息交换速度慢,导致解的时间更长。另一方面,当有太多的青蛙被选中时,青蛙就会被不想要的想法感染,这些想法会触发审查现象,从而延长搜索时间。
第四个参数N,可以取任何大于1的值。如果N很小,memeplexes将经常被打乱,减少了局部范围的想法交流。另一方面,如果N很大,那么每个memeplex将被压缩为一个局部优化。
第五个参数,Smax,是被感染后被青蛙所允许的最大的步长。Smax实际上是控制SFLA全局探索能力的一个约束条件。将Smax设置为一个小值会降低全局探测能力,从而使算法更倾向于局部搜索。
另一方面,一个大的Smax可能会导致缺少实际的优化,因为它没有经过微调。
五、实验评估
对于每个测试问题,总共执行了20次运行SFLA参数的不同组合的运行。
在每一次运行中,停止的标准是至少有一只青蛙会在连续10次循环(洗牌)中携带“迄今为止最好的记忆模式”。
在95%的运行中,标准被满足了,尽管在运行和问题之间需要的功能评估的数量是不同的。
为了进行比较,测试函数还可以使用基于ga的优化器Evolver(1997)来解决。不同的初始基因组合,种群数量,交叉和突变率,每个组合运行20次。在每一次运行中,停止的标准是,最好的函数值是连续10代不会改变的。在20%的情况下,GA没有找到最优值。图5总结了SFLA和GA对测试函数的比较。垂直条表示在成功运行中找到全局最优值的平均次数。
为了对SFLA进行更健壮的测试,我们选择使用SFLA和GA(见附录A),选择并解决了另一组具有离散变量的六种成熟的测试函数。
这些函数和SFLA参数选择的影响比第一组更详细地分析了SFLA在寻找全局最佳解决方案时的鲁棒性,以及在寻找全局解决方案所需的函数评估的数量方面的效率。
不同的参数值改变了聚合到全局最优值的机会,但也会改变所需的函数评估的数量。
因此,计算成本和成功的概率之间的妥协是必要的。
- 在实验中,memeplexes的m值在10到50之间变化,增量为10。从70到100,增量为30。
- 在每一种memeplex中青蛙的数量n是10、20,30、40、50、70、100、150、200和300。
- 在submemeplex中,青蛙的数量q在5到20之间变化,增量为5,洗牌阶段的N从5增加到35,增量为5。
除了Simpleton25和Simpleton50问题之外,所有问题都使用了相同的参数范围。研究发现,从10到100的m值,Simpleton25和Simpleton 50的最优值很难实现。因此,对于这两个问题m的范围被扩展到300。
————————————————————————————————————————————————————————————
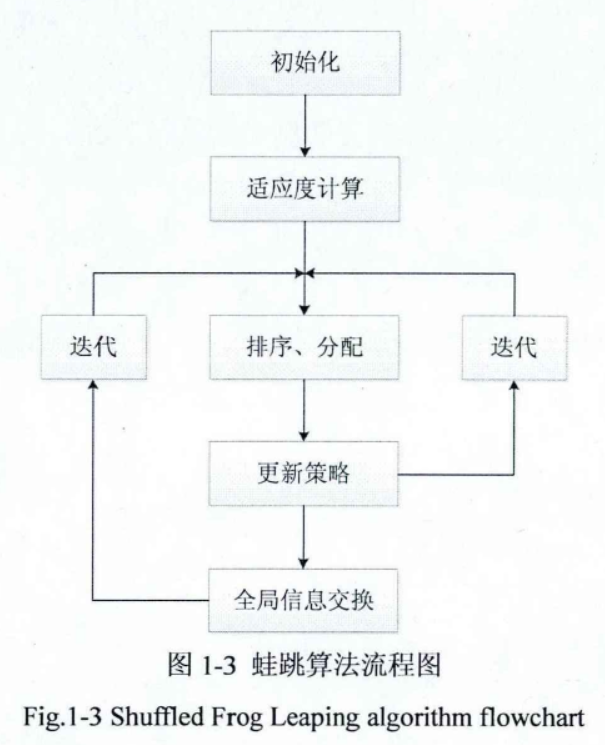
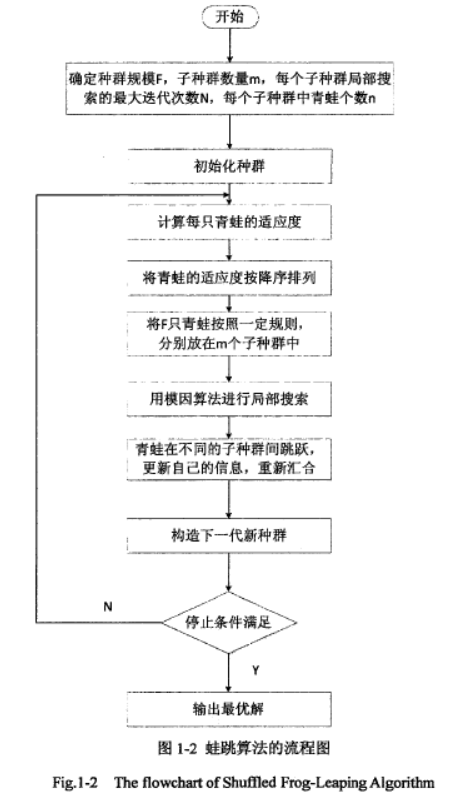
第一步:确定种群规模F,子种群数量m,每个子种群中的青蛙个数n,每个子种群局部搜索的最大迭代次数N。F=mn。
第二步:计算每只青蛙的适应度
第三步:将青蛙的适应度按降序排列
第四步:将F只青蛙按照一定规则,分别放在m个子群中
第五步:用模因算法进行局部搜索
第六步:青蛙在不同的子种群间跳跃,更新自己的信息,重新汇合
第七步:构造下一代新种群
第八步:满足停止条件输出最优解,否则回到第二步
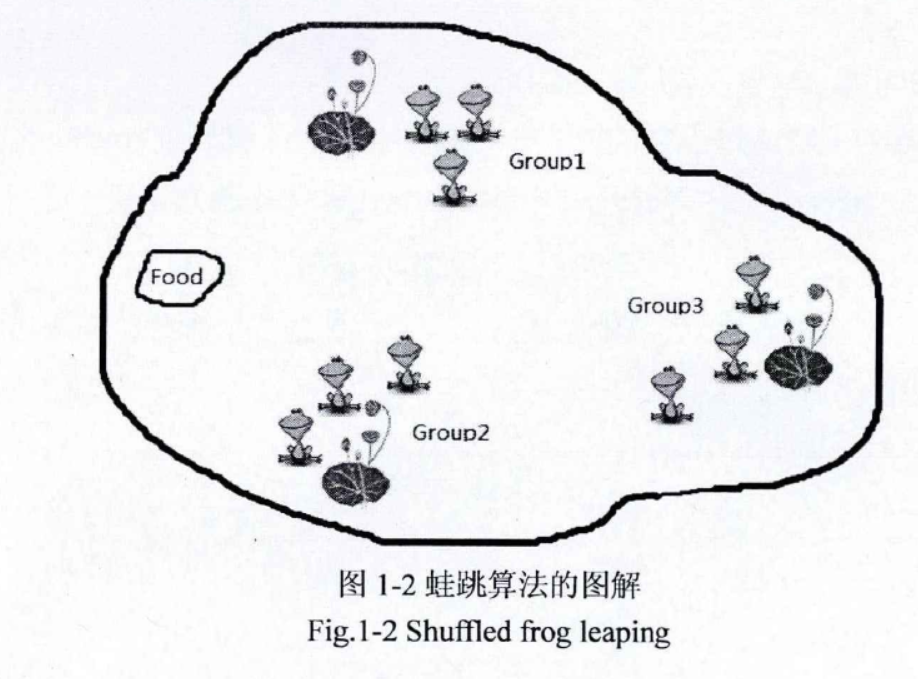
每只青蛙表示一个可行解。每个子群分别进行局部搜索。