matlab练习程序（直方图反向投影）

　　做meanshift物体跟踪的时候中间有一步叫做直方图反向投影，所以我就先实现了这样一个步骤。

　　直方图反向投影说白了就是模板匹配，给定一个较小的目标模板，然后再逐个遍历原图像和模板图像相同的图像块的，对比图像块和模板的直方图，然后把比较结果存入一个新的图像中，新图像中的全局极值就是模板在原图像中所在的位置。这里主要麻烦的是怎么比较两个图像块的直方图，Opencv中实现了5种对比的方法，所以我在这里也对应的实现了5种方法。

　　5种方法分别是correl（相关）、chisqr（卡方）、intersect（相交）、bhattacharyya（名字很长--!!）、emd（earth mover's distance）。

　　下面是这5种方法的公式，H1是第一个图像块的直方图序列，H2是第二的图像块的直方图序列：

　　相关法：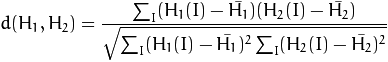

　　其中：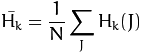

　　卡方法：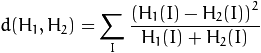

　　相交法：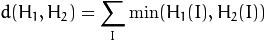

　　bhattacharyya: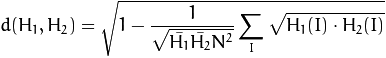

　　emd:

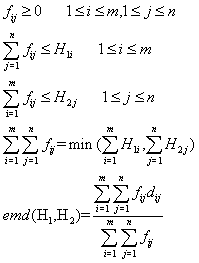
　　前4种方法比较简单，emd就比较麻烦了，下面是我自己的理解。这个算法使用原序列生成f和d这两个矩阵，然后对这两个矩阵进行处理。d矩阵按我的理解就是H1中各个元素和H2中各个元素在位置上的距离，比如H1和H2都是只有三个元素的序列，H1(1)和H2(1)的距离就是0，所以d(1,1)=0，H1(3)和H2(2)的距离是1，所以d(3,2)=1，以此d=[0 1 2;1 0 1;2 1 0]，这里d和H1，H2中的值没关系。f的确定就比较麻烦了，看看约束条件就让人头疼了。按照约束条件是没办法写程序的，不过我想到一个巧妙的方法求的的结果正好满足那四个约束条件：首先不管前三个条件，只使用第四个条件求得矩阵f，然后对f从最右列开始依次减去相邻的左边的列，然后对f从最下行开始依次减去相邻的上边的行，求得的结果正好满足条件。至于为什么这样我还不得其解，原因就指望哪位数学大牛去探索吧。

　　下面是代码：

　　main.m

close all;
clear all;
clc;

img=imread('lena.jpg');
imshow(img);
[m n]=size(img);

w=imcrop();      %这里把要裁剪的图像框出来
[H W]=size(w);
hist1=histcount(w);

HH=floor(H/2);
WW=floor(W/2);

imgn=zeros(m+2*HH+1,n+2*WW+1);
imgn(HH+1:m+HH,WW+1:n+WW)=img;
imgn(1:HH,WW+1:n+WW)=img(1:HH,1:n); 
imgn(1:m+HH,n+WW+1:n+2*WW+1)=imgn(1:m+HH,n:n+WW);
imgn(m+HH+1:m+2*HH+1,WW+1:n+2*WW+1)=imgn(m:m+HH,WW+1:n+2*WW+1);
imgn(1:m+2*HH+1,1:WW)=imgn(1:m+2*HH+1,WW+1:2*WW);

re1=imgn;
re2=imgn;
re3=imgn;
re4=imgn;
re5=imgn;
for i=HH+1:m+HH
    for j=WW+1:n+WW
        s=imgn(i-HH:i+HH,j-WW:j+WW);
        hist2=histcount(s);
     
        re1(i,j)=correl(hist1,hist2);           %相关法
        re2(i,j)=chisqr(hist1,hist2);           %卡方法
        re3(i,j)=intersect(hist1,hist2);        %相交法
        re4(i,j)=bhattacharyya(hist1,hist2);    %名字很长的法
        re5(i,j)=emd(hist1,hist2);     %由于没有优化，速度实在太慢了，至少运行一晚上，慎用！！
    end
end
figure;
re1=re1(HH+1:m+HH,WW+1:n+WW);
imshow(mat2gray(re1));

figure;
re2=re2(HH+1:m+HH,WW+1:n+WW);
imshow(mat2gray(re2));

figure;
re3=re3(HH+1:m+HH,WW+1:n+WW);
imshow(mat2gray(re3));

figure;
re4=re4(HH+1:m+HH,WW+1:n+WW);
imshow(mat2gray(re4));

figure;
re5=re5(HH+1:m+HH,WW+1:n+WW);
imshow(mat2gray(re5));

　　histcount.m 统计直方图

function hist=histcount(w)
    [H W]=size(w);
    w=uint8(w);
    hist=zeros(1,256);
    for i=1:H
        for j=1:W
            hist(w(i,j)+1)=hist(w(i,j)+1)+1;
        end
    end

    hist=hist/(H*W);

end

　　correl.m 相关法

function d=correl(H1,H2)
    d=sum(H1-mean(H1).*(H2-mean(H2)))/sqrt(sum((H1-mean(H1)).^2)*sum((H2-mean(H2)).^2));
end

　　chisqr.m 卡方法

function d=chisqr(H1,H2)
    d=sum(((H1-H2).^2)/(H1+H2));
end

　　intersect.m 相交法

function d=intersect(H1,H2)    
    d=sum(min(H1,H2));
end

　　bhattacharyya.m

function d=bhattacharyya(H1,H2)
    d=sqrt(1-sum(sqrt(H1.*H2))/sqrt(sum(H1)*sum(H2)));
end

　　emd.m 这里没优化，慎用！

function re=emd(H1,H2)
    m=length(H1);
    n=length(H2);
    f=zeros(m,n);
    d=zeros(m,n);
    
    for i=1:m
        for j=1:n
            if i==j
                d(i,j)=0;
            end       
            if j>i
                d(i,j)=j-i;
            end       
            if j<i
                d(i,j)=i-j;
            end    
            f(i,j)=min(sum(H1(1:i)),sum(H2(1:j)));              
        end   
    end
    
    for i=m:-1:2
        f(:,i)=f(:,i)-f(:,i-1);
    end
    
    for j=n:-1:2
        f(j,:)=f(j,:)-f(j-1,:);
    end

    re=(sum(sum(f.*d)))/sum(sum(f));
    
end

　　下面是运行效果：

原图

使用的模板，就是lena的右眼。

Dsp Tian

matlab练习程序（直方图反向投影）

公告