《软工实践》个人项目 - 数独棋盘
《软工实践》个人项目 - 数独棋盘
Github项目地址
https://github.com/thousfeet/Sudoku
PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 10 | 5 |
| · Estimate | · 估计这个任务需要多少时间 | 10 | 5 |
| Development | 开发 | 1245 | 1295 |
| · Analysis | · 需求分析 (包括学习新技术) | 4h * 60 | 5h * 60 |
| · Design Spec | · 生成设计文档 | 30 | 40 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 5 | 5 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 20 | 10 |
| · Design | · 具体设计 | 30 | 30 |
| · Coding | · 具体编码 | 10h * 60 | 9h * 60 |
| · Code Review | · 代码复审 | 30 | 40 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 5h * 60 | 5.5h * 60 |
| Reporting | 报告 | 60 | 60 |
| · Test Report | · 测试报告 | 20 | 30 |
| · Size Measurement | · 计算工作量 | 10 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 20 |
| 合计 | 1315 | 1360 |
项目要求
1.目标:随机生成n个已解答完毕的的数独棋盘矩阵,并输出到当前路径下的‘sudoku.txt’文件中;当输入参数有误时需进行错误处理,给出提示信息。
2.约束:各矩阵不重复;矩阵的第一个元素为5( (2+2)%9+1 );数量n的范围是0-1000000;当n<1000时,运行时间不超过1min。
解题思路
最容易想到的做法就是慢慢枚举,从第二位开始放入一个数判断下满足与否,不满足就换一个数,都无法满足就回溯。但是回溯法的复杂度是指数或者阶乘级别的,整个运行起来会非常的慢,想要在60s内得到1000个,10min内得到100w个矩阵基本是不可能了。
考虑到效率问题,最快的办法就是把所有满足要求的解都存下来然后随机抽取。然而稍微查一下就会发现,数独棋盘的总数为9! × 722 × 27 × 27704267971,总共有 6,670,903,752,021,072,936,960 这么多。即使是第一项为5,仍然有 6670903752021072936960 ÷ 9 = 741211528002341437440。一个小程序占这么大空间显然是非常不友好的。
查找各种资料,后来发现一种做法,权且称之为魔方算法。也就是先拿出一个已完成的数独棋盘作为初始矩阵,然后像玩魔方那样的对其进行各种变换,变换时不能改变数独棋盘本身的特性,即满足每行、每列、每宫都有1-9这9个数字。为了说明如何变换,下文把每三行称作一大行,每三列称作一大列,也即每个棋盘有三大行、三大列。
可以得知,满足条件的变换有:
1.交换任意两个数字的位置,如把所有值为1的和值为2的元素位置进行调换。
2.交换任意某一大行中的任意某两行的位置。
3.交换任意某一大列中的任意某两列的位置。
4.交换任意两大行。
5.交换任意两大列。
而总共要做哪些变换、每次变换时的交换哪些数字或哪些行列都可以用随机数产生。
然而,由于有随机的因素在,并不能像前两种做法那样保证完全满足矩阵之间互不重复的要求。
下面说明该做法的正确性:
考虑每生成一个矩阵只做一次变换,那么最坏的情况下,会有 2/5 * 1/3 * 1/3 = 2/45 做相同的变换从而导致重复,乘上1000000也即会有几万个相同矩阵。而实际上上产生重复的概率还会比计算略大一些。
若变换次数多一些,比如每生成一个矩阵做十次变换,那么大约有(2/45)^10概率做完全相同的变换而导致重复。此时即使实际中的这个概率会偏大一些,但已经较难得到重复的矩阵了。
因此,只要变换次数多一些,使得重复概率乘上要生成的矩阵个数远远小于1,就能保证在一定的数量范围内不会重复。在代码中我取变换次数为50。
当然,这样得到的正确性是建立在满足条件的矩阵总个数非常之多的前提下的,也即可以认为如果不是按相同的方式变换几乎得不到两个完全相同的矩阵。
用这种做法每产生一个矩阵所用时间都为常数,总复杂度为O(N),试运行得到1000个矩阵只要30s不到的时间。
但由于概率事件最终结果会怎么样不可预估,如果改作业的时候真的跑出来重复矩阵那大概是运气不行(
9.12 更新:终于闲下来,早上试了试判重,100w会出10多个重复。推论的误差有点大。目前的解决方案就是多生成n*0.1个矩阵,然后去重(见后文)。
设计实现
一、总体设计
1.读取命令行参数。若参数有误时,输出“Arguments error”,退出程序。若无误,则开始后续处理。
2.生成数独矩阵的算法为:进行n次循环,每次循环得到一个随机矩阵。得到的方式为随机地对初始数独矩阵进行若干次变换:数字间交换、交换大三行中的小行、交换大三列中的小列、交换大三行、交换大三列。
二、具体程序设计
1.主程序为sudoku.cpp,另有两个类:sudokuMat、changeTool。主程序中做的事为:判断参数无误后,调用sudokuMat类中的函数randomMat,将待生成的矩阵个数n传入。
2.初始矩阵作为私有成员变量保存在sudokuMat类中,该类除构造函数外含有两个公有成员函数getMat和randomMat,其中:
| 函数 | 输入 | 输出 | 功能 |
|---|---|---|---|
| void getMat(); | void | void | 循环50次,每次随机调用changeTool类中的变换函数,对初始矩阵进行变换。其中,传入变换函数的参数也是随机生成的。随机变换结束后,调用changeTool类中的check函数,和printMat函数输出最终矩阵。 |
| void randomMat(int n); | int n:待生成的矩阵个数 | void | 循环n次,每次调用getMat获取生成矩阵 |
3.changeTool作为变换函数工具类,除构造函数含有公有成员函数swapNumber、swapRow、swapCol、swap3Row、swap3Col、check、printMat。
| 函数 | 输入 | 输出 | 功能 |
|---|---|---|---|
| void swapNumber(int num1,int num2); | int num1,int num2:待交换的两个数字 | void | 矩阵中所有值为num1的元素和值为num2的元素位置互换 |
| void swapRow(int i, int row1, int row2); | int i:用于确定待交换的是第几大行; int row1, int row2:用于确定待交换的小行下标 | void | 交换第i大行中,第row1%3行与第row2%3行的元素 |
| void swapCol(int i, int col1, int col2); | int i:用于确定待交换的是第几大列; int col1, int col2:用于确定待交换的小列下标 | void | 交换第i大列中,第col1%3行与第col2%3列的元素 |
| void swap3Row(int squ1, int squ2); | int squ1, int squ2:待交换的两大行的下标 | void | 交换第squ1大行与squ2大行的所有元素 |
| void swap3Col(int squ1, int squ2); | int squ1, int squ2:待交换的两大列的下标 | void | 交换第squ1大列与squ2大列的所有元素 |
| void check(); | void | void | 通过交换矩阵中所有值为5的,和所有值为矩阵第一位元素的位置,对第一位元素非5的情况进行修正 |
| void printMat(); | void | void | 将最终矩阵输出到sudoku.txt中 |
代码说明
随机生成并打印一个数独矩阵:(位于sudokuMat.cpp)
void sudokuMat::getMat()
{
changeTool ct(initMat);
int changeTime = changeTimes; //循环次数为50次
int changeOption; //随机变换类型
int i,a,b; //随机传入参数
while (changeTime--)
{
changeOption = rand()%5;
switch (changeOption)
{
case 0: //变换类型为0时进行数字交换
a = rand() % 9 + 1;
b = rand() % 9 + 1;
if(a!=b) ct.swapNumber(a, b);
break;
case 1: //变换类型为1时进行行交换
i = rand() % 3;
a = rand();
b = rand();
if (a != b) ct.swapRow(i, a, b);
break;
case 2: //变换类型为2时进行列交换
i = rand() % 3;
a = rand();
b = rand();
if (a != b) ct.swapCol(i, a, b);
break;
case 3: //变换类型为3时进行大行交换
a = rand() % 3;
b = rand() % 3;
if (a != b )ct.swap3Row(a, b);
break;
case 4: //变换类型为3时进行大列交换
a = rand() % 3;
b = rand() % 3;
if (a != b) ct.swap3Col(a, b);
break;
default:
a = rand() % 9 + 1;
b = rand() % 9 + 1;
if (a != b) ct.swapNumber(a, b);
break;
}
}
ct.check(); //修正第一项不为5的情况
ct.printMat(); //打印输出最终矩阵
}
测试运行
以上的初版完成之后进行试运行:


单元测试通过:

代码覆盖率:
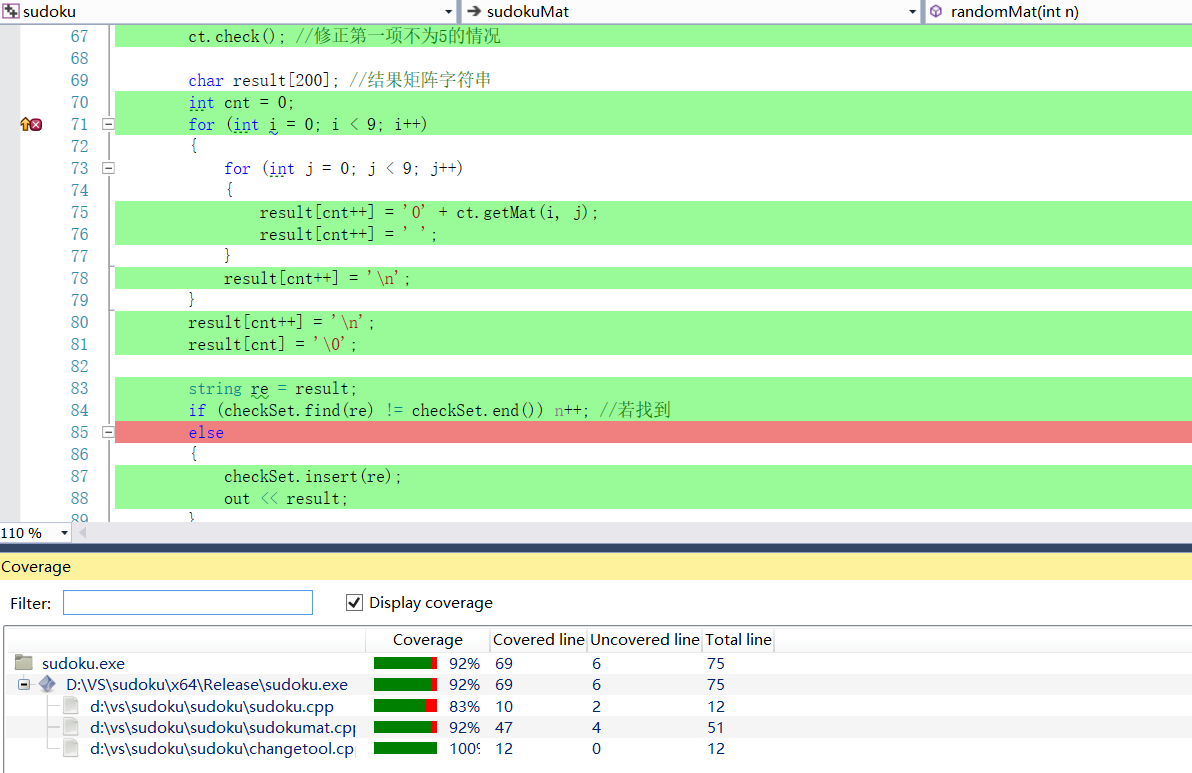
性能分析与改进
version 1
- n = 200 的CPU时间 : 3.861秒

- n = 1000 的CPU时间 : 27.012秒

虽说是以快一倍的时间达到了60s内出1000的要求,但得知助教学长测试100w数据的时候将会是以 10min喊停、60min至多 的标准,细思恐极,按现在这样的速度要出100w的话要500min!
再一推算,想要在60min内完成100w的话,出1000需要在3.6s内完成;想要10min内完成的话,出1000需要在0.6s内!(吃鲸
赶紧开始性能分析。
- 性能分析
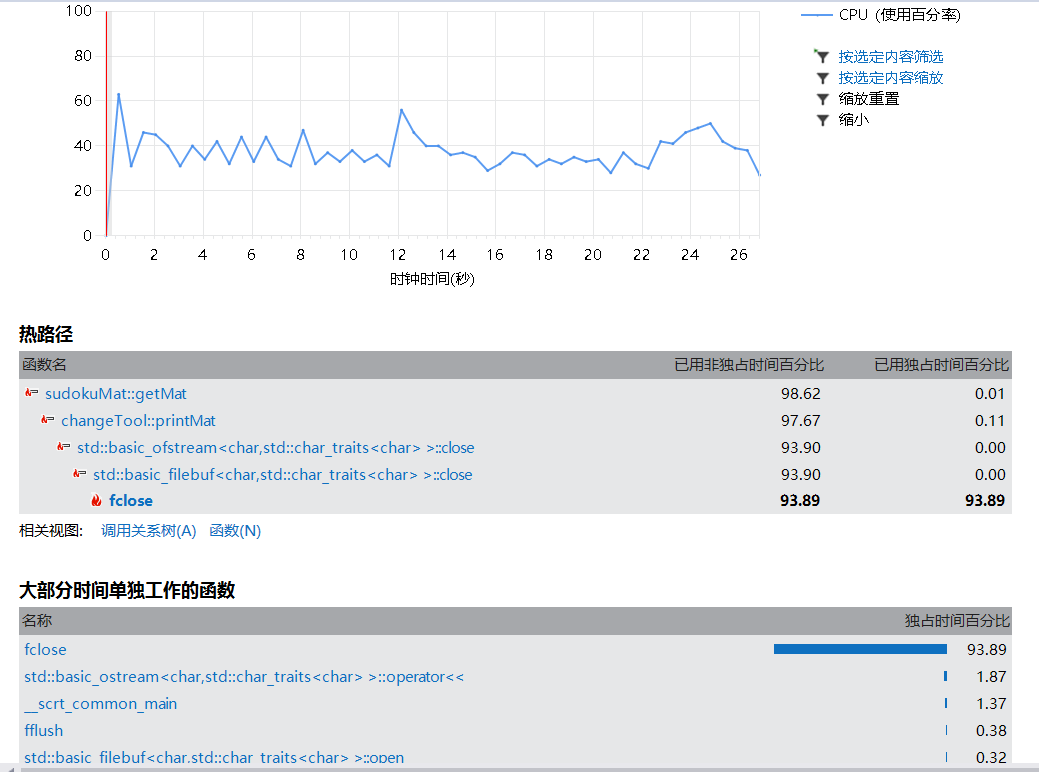
没想到文件操作用了这么多的时间!
逐步点进去查看:
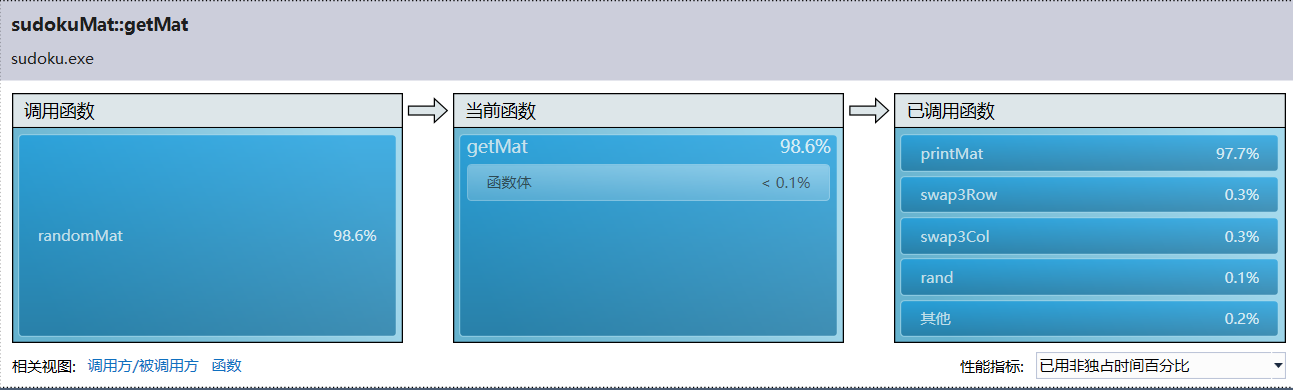

是关闭文件的操作花了很多时间。再查看代码,发现我每输出一个矩阵都要对文件做一次打开和关闭的操作,输出100w的话就要关闭100w次,难怪这么慢。
于是修改了一下代码,把getMat内部代码直接贴到randomMat的while循环内部,而在循环的外部做文件的打开的关闭操作。
version 2,8分43秒
修改完之后:
- n = 1000 的CPU时间 : 2.792秒

- n = 100w 的CPU时间 : 8分43秒

看上去似乎能满足要求了,奇怪的是为什么运行1000需要将近3s而运行100w却只用了8分多钟呢(
- 性能分析

除了swap3Col之外都是库函数,于是点进这个函数查看:
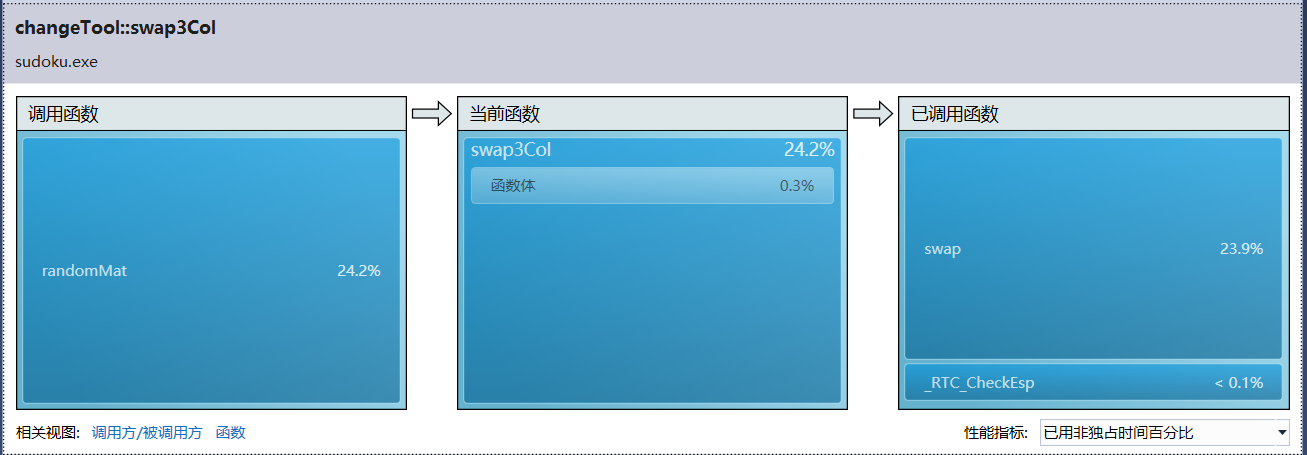
发现其实是swap函数用时最多。
点进函数界面细看,果然是如此:

但是swap函数本身已经做了很多速度上的优化,自己去重写swap似乎意义不大。想了想,可以在swap前加上if判断语句,如果二者不同的话再做swap。
version 3,1分48秒
修改完之后:
- n = 1000 的CPU时间 : 2.589秒

- n = 100w 的CPU时间 : 1分48秒

出100w只用108秒!!(*>∀<)ノ))★ (不过这次用的是release版本而非debug版本)
- 性能分析
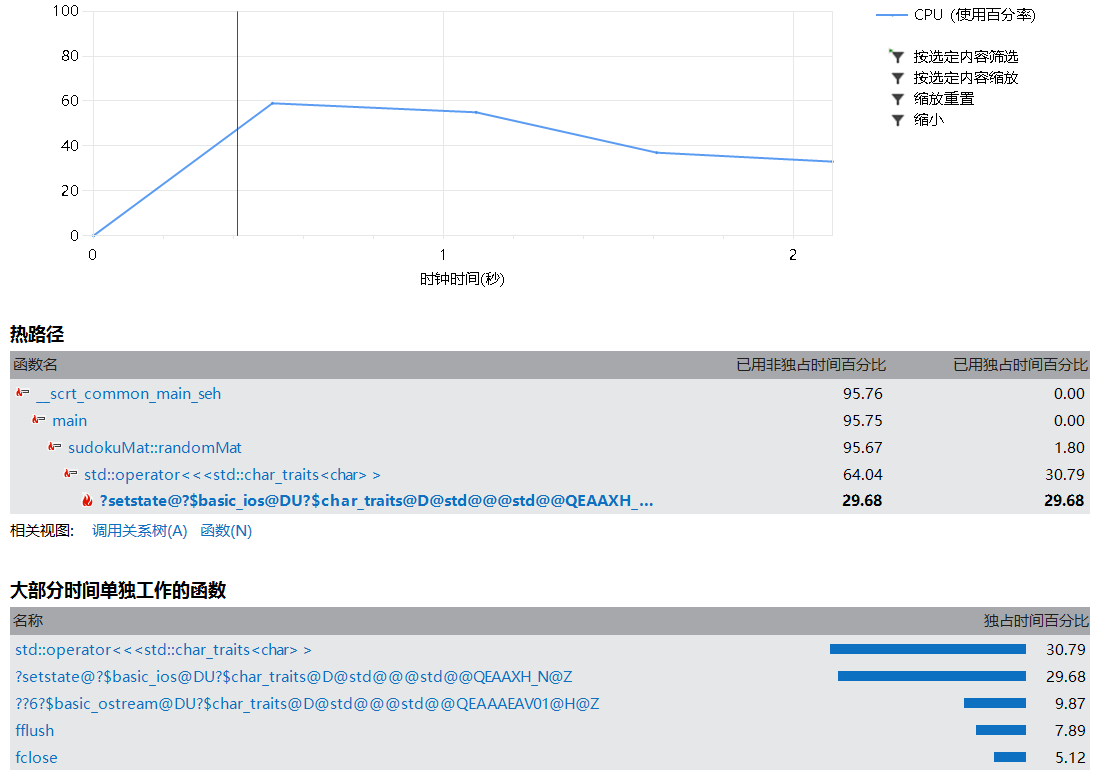
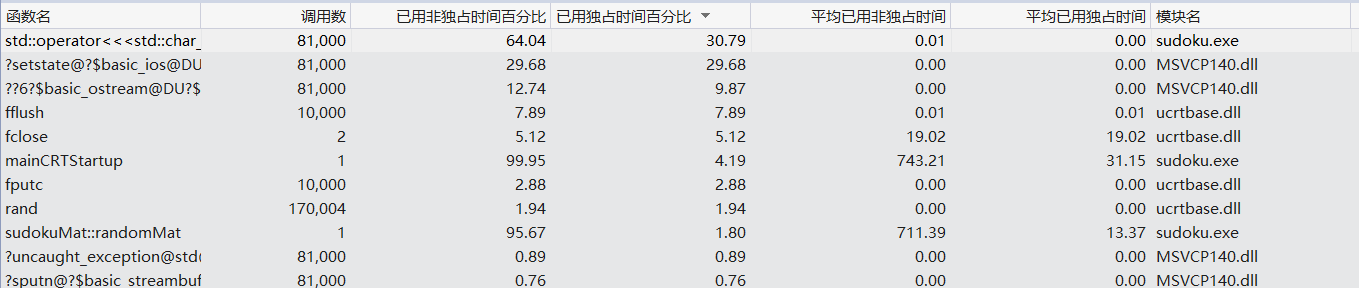
现在用时最多的是用文件流输出数据的操作了。
version 4,10.844s
刚瞟了一眼别的同学的博客,1s出100w...原来竟然是可以快到这个程度的吗,都不知道前面在激动什么2333(
这次修改了一下version 2中的输出问题,改成先用字符串存下整个矩阵再一并文件流输出。
- n = 100w 的CPU时间 : 10.844秒

提升了不少,但离1s还有差距。
- 性能分析
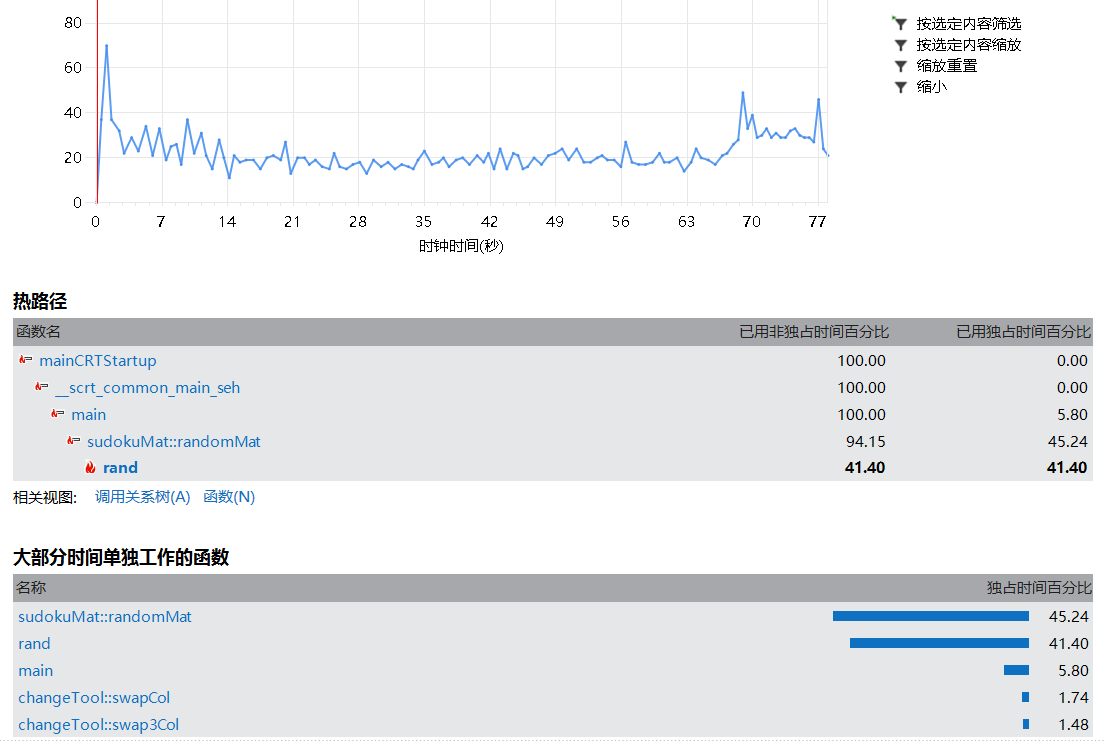
(因为时间所限暂时没有做附加题,如果有可能之后再补上。)
【9.13更新】
推断错误,还是出现了重复矩阵,所以加入了去重代码(8行)。
version 5 ,9.286s
纠错的方法是每次判重,若生成一个不重复矩阵就加入set,若重复,待生成的矩阵个数n++。
set<string> checkSet;
string re = result;
if (checkSet.find(re) != checkSet.end()) n++; //若找到
else
{
checkSet.insert(re);
out << result;
}

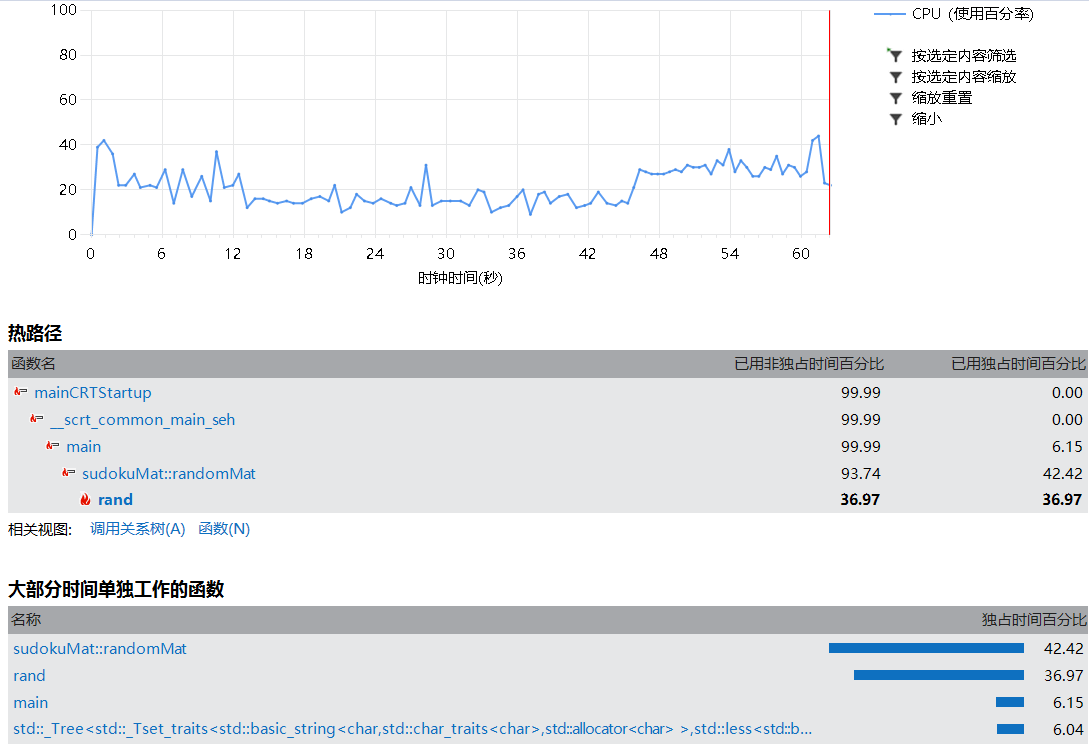
因为有了判重,速度就降低了。
考虑到,既然有了判重,变换次数其实就可以减少一些。再一细想,变换次数和判重这两件事最终应当会达到一个平衡:也即变换次数m增多的话,出现重复矩阵而使得n增多的概率更小;变换次数减少的话,出现重复矩阵使得n增多的概率更大。
所以手动二分法一下,去找一个合适的变换次数m使得速度最优。
m = 30

m = 20

m = 10

然后在10和20之间二分尝试,最后结果是m = 19的时候最优。

记录自己的学习进度条(每周追加)
| 周 | 新增代码(行) | 累计代码(行) | 本周学习耗时(小时) | 累计学习耗时(小时) | 重要成长 |
|---|---|---|---|---|---|
| 1 | 405 | 405 | 22 | 22 | 了解了PSP开发流程并完成了一个c++个人项目,从而熟悉了visual studio开发环境,以及对git有了更多的认识 |
| … |
---


 浙公网安备 33010602011771号
浙公网安备 33010602011771号