阿里巴巴集团2014校园招聘笔试题（研发工程师--北邮站）

原文地址：http://blog.sina.com.cn/s/blog_6f83fdb40101eyzw.html

阿里巴巴集团2014校园招聘笔试题

（9月22北邮站）

(答案仅是个人见解，欢迎补充更正，谢谢)

第一部分 单选题（前10题，每题2分；后10题，每题3分。选对得满分，选错倒扣1分，不选得0分）

1、一次内存访问，SSD硬盘访问和SATA硬盘随机访问的时间分别是（C）

A、几微秒，几毫秒，几十毫秒 B、几十纳秒，几十微秒，几十毫秒

C、几十纳秒，几十微秒，几十毫秒 D、几微秒，几十微秒，几十毫秒

2、8进制数256，转化成7进制数是（B）

A、356 B、336 C、338 D、346

3、某网络的IP地址空间为192.168.5.0/24，采用定长子网划分，子网掩码为255.255.255.248，则该网络的最大子网个数、每个子网内最大可分配地址个数各位（C）

A、8,32 B、32,8 C、32,6 D、8,30

4、以下关于链式存储结构说法错误的是（A）

A、查找节点时链式存储比顺序存储快

B、每个节点是由数据域和指针域组成

C、比顺序存储结构的存储密度小

D、逻辑上不相邻的节点物理上可能相邻

5、假定一个二维数组的定义语句为“int a[3][4]={{3,4},{2,8,6}};”，则元素a[1][2]的值为（A）

A、6 B、4 C、2 D、8

6、下面函数的功能是（C）

int fun (char *s)

{

char *p=s;

while(*p++);

return p-s-1;

}

A、计算字符串的位(bit)数 B、复制一个字符串

C、求字符串的长度 D、求字符串存放的位置

7、判断有向图是否存在回路，利用（A）方法最佳

A、拓扑排序 B、求最短路径

C、求关键路径 D、广度优先遍历

8、依次读入数据元素序列{a,b,c,d,e,f,g}进栈，元素进栈或出栈顺序是未知的，下列序列中，不可能成为栈空时弹出的元素构成序列的有（D）

A、{d,e,c,f,b,g,a} B、{c,d,b,e,f,a,g} C、{e,f,d,g,c,b,a} D、{f,e,g,d,a,c,b}

9、下列有关图的遍历说法中，不正确的是（C）

A、有向图和无向图都可以进行遍历操作

B、基本遍历算法两种：深度遍历和广度遍历

C、图的遍历必须用递归实现

D、图的遍历算法可以执行在有回路的图中

10、在16位机器上跑下列foo函数的结果是（B）

void foo()

{

int i = 65536;

cout << i <<”,”;

i = 65535;

cout << i;

}

A、-1,65535 B、0,-1 C、-1,-1 D、0,65535

11、有一段年代久远的C++代码，内部逻辑复杂，现在需要利用其实现一个新的需求，假定有以下可行的方案，应当优先选择（D）

A、修改老代码的接口，满足新的需求

B、将老代码抛弃，自己重新实现类似的逻辑

C、修改老代码的内部逻辑，满足新的需求

D、在这段代码之外写一段代码，调用该代码的一些模块，完成新功能需求

12、在5个页框上使用LRU页面替换算法，当页框初始为空时，引用序列为0、1、7、8、6、2、3、7、2、9、8、1、0、2，系统将发生（C）次缺页

A、13 B、12 C、11 D、8

分析：缺页为：0、1、7、8、6、2、3、9、8、1、0，共11次

13、阿里巴巴有相距1500km的机房A和B，现有100GB数据需要通过一条FTP连接在100s的时间内从A传输到B。已知FTP连接建立在TCP协议之上，而TCP协议通过ACK来确认每个数据包是否正确传送。网络信号传输速度2*10⁸m/s，假设机房间带宽足够高，那么A节点的发送缓冲区可以设置为最小（A）

A、18M B、12M C、6M D、24M

分析：

TCP协议原理：TCP每发送一个报文段，就启动一个定时器，如果在定时器超时之后还没有收到ACK确认，就重传该报文。

如图所示，数据包由A的缓冲区发往B，B在收到数据包以后，回发一个ACK确认包给A，之后A将该数据包从缓冲区释放。因此，该数据包会一直缓存在A的缓冲区，直到一个ACK确认为止。题目要求在100s内发送100GB数据，网络的传输速率至少是1G/s，某个数据包n在A中缓存的时间就是数据包n从A到B，再加上该数据包的ACK从B到A的时间：2*1500km/(2*10⁸m/s)=1.5*10^-2s，该段时间A中缓存的数据量至少是1G/s*1.5*10^-2s约为15M

14、有3个节点的二叉树可能有（A）种

A、5 B、13 C、12 D、15

15、设某文件经内排序后得到100个初始归并段（初始顺串），若使用多路归并排序算法，且要求三趟归并完成排序，问归并路数最少为（D）

A、8 B、7 C、6 D、5

分析：m个元素k路归并的归并趟数s=log_k(m)，代入数据：log_k(100)≦3

16、一个优化的程序可以生成一n个元素集合的所有子集，那么该程序的时间复杂度是（B）

A、O(n!) B、O(2ⁿ) C、O(n²) D、O(n log n)

17、快速排序在已经有序的情况下效率最差，复杂度为（B）

A、O(n log n) B、O(n²) C、O(n^1.5) D、O(n² log n)

18、从一副牌(52张，不含打小怪)里抽出两张牌，其中一红一黑的概率是（D）

A、25/51 B、1/3 C、1/2 D、26/51

分析：52张牌从中抽两张，就是C₅₂²种情况，一红一黑是C₂₆¹ * C₂₆¹种情况，概率P = C₂₆¹ * C₂₆¹ / C₅₂² =26/51

19、有一堆石子共100枚，甲乙轮流从该堆中取石子，每次可取2、4或6枚，若取得最后的石子的玩家为赢，若甲先取，则（C）

A、谁都无法取胜 B、乙必胜 C、甲必胜 D、不确定

分析：先取的人只需要保证最后剩8枚就胜了。而要保证最后剩8枚，则必须要保证每一个回合内取的数是一个可控的固定数，显然这个数字是8，所以只需要保证第一次取完后，剩下的数字是8的倍数，就一定能胜。100除以8余数为4，故而，甲先取4枚，之后每一个回合所取数与上一个回合乙所取数之和为8，就能保证必胜。

20、现有一完全的P2P共享协议，每次两个节点通讯后都能获取对方已经获取的全部信息，现在使得系统中每个节点都知道所有节点的文件信息，共17个节点，假设只能通过多次两个对等节点之间通讯的方式，则最少需要（C）次通讯

A、32 B、31 C、30 D、29

解法由@龙人920提供

分析：如上图1所示，假设有5个节点，按连线1、2、3、4通讯之后，节点4和5就掌握了所有节点的信息，之后，1、2、3节点只需跟4或5任一节点通讯一次即连线5、6、7就可保证每个节点都知道所有节点的信息，总的通讯次数是(n-1)+(n-2)=2n-3次。

如果将所有节点分成两组，如图2所示，两组中的节点分别按连线1-8顺序通讯之后，节点4和5就掌握了1-5所有节点的信息，节点9和0就掌握了6-0所有节点的信息，再按连线9、10通讯之后，节点4、5、9、0就掌握了1-0所有节点的信息，剩下的节点只需跟4、5、9、0任一节点通讯一次就可保证每个节点知道所有节点信息，和图1相比，多了9和10两次通讯，总的通讯次数是(2n₁-3)+(2n₂-3)+2=2n-4次(n₁和n₂分别表示分组中元素个数)。

分3组的情况是(2n₁-3)+(2n₂-3)+(2n₃-3)+6=2n-3次

分4组的情况是(2n₁-3)+(2n₂-3)+(2n₃-3)+(2n₄-3)+8=2n-4次

第二部分 不定项选择（每题五分，每题有1-5个正确选项，完全正确计5分，漏选计2分不选计0分，多选、错选计-2分）

21、2-3树是一种特殊的树，它满足两个条件：

（1）每个内部节点有两个或三个子节点；

（2）所有的叶节点到根的路径长度相同；

如果一颗2-3树有9个叶节点，下列数量个非叶节点的2-3树可能存在的有（BE）

A、8 B、7 C、6 D、5 E、4

分析：根据条件(2)，叶节点只能在同一层，根据条件(1)，上一层的父节点只能是3个或4个，只能是如下图所示的两种结果

22、下列有关进程的说法中，错误的是（ABC）

A、进程与程序是一亿对应的 B、进程与作业时一一对应的

C、进程是静态的 D、进程是动态的过程

23、下列函数定义中，有语法错误的是（D）

A、void fun(int x, int *y){x *= *y;}

B、int * fun(int *x, int y){return x += y;}

C、void fun(int *x, int y){*x += y;}

D、void fun(int x, int *y){*x *= *y;}

24、有朋自远方来，他乘火车，轮船，汽车，飞机来的概率分别是0.3,0.2,0.1,0.4，坐各交通工具迟到的概率分别是1/4,1/3,1/12,0，下列语句中正确的是（CD）

A、如果他准点，那么乘飞机的概率大于等于0.5

B、坐陆路（火车，汽车）交通工具准点机会比坐水路（轮船）要低

C、如果他迟到，乘火车的概率是0.5

D、如果他准点，坐轮船或汽车的概率等于坐火车的概率

第三部分 填空与问答

25、（4分）文件分配表FAT是管理磁盘空间的一种数据结构，用在以链接方式存储文件的系统中记录磁盘分配和追踪空白磁盘块，整个磁盘仅设一张FAT表，其结构如下所示，如果文件块号为2，查找FAT序号为2的内容得知物理块2的后继物理块是5，再查FAT序号为5的内容得知物理块5的后继物理块是7，接着继续查FAT序号为7的内容为“Λ”，即该文件结束标志，

假设磁盘物理块大小为1KB，并且FAT序号以4bits为单位向上扩充空间。请计算下列两块磁盘的FAT最少需要占用多大的存储空间？

（1）一块540MB的硬盘（2）一块1.2GB的硬盘

分析：（1）磁盘块大小为1KB，540MB的硬盘可以分成540MB/1KB=5.4*10⁵个磁盘块，因此至少需要5.4*10⁵<2²⁰个编号，需要20bit存储空间

（2）同理，1.2G至少需要1.2*10⁶<2²¹个编号，为21bit，由于FAT序号以4bits为单位向上扩充，因此需要24bit存储空间

26、（4分）已知如下代码，并在两个线程中同时执行f1和f2，待两个函数都返回后，a的所有可能值是哪些？

int a = 2, b = 0, c = 0;

void f1() void f2()

{ {

b = a * 2; c = a + 11;

a = b; a = c;

} }

分析：考虑四行代码的执行顺序即可

（1）b=a*2,c=a+11,a=c,a=b a=4

（2）b=a*2,c=a+11,a=b,a=c a=13

（3）b=a*2,a=b,c=a+11,a=c a=15

（4）c=a+11,a=c,b=a*2,a=b a=26

27、（6分）设计一个最优算法来查找一n个元素数组中的最大值和最小值，已知一种需要比较2n次的方法，请给一个更优的算法。请特别注意优化时间复杂度的常数。

给出该算法最坏情况下的比较次数和该算法的步骤描述。（不用写代码，不给出比较次数的不得分）

分析：已知的比较2n次的方法，显然是将每个元素和最大值、最小值各比一次，要减少比较次数，可以有多种优化方法：

方法一：一个元素先和最大值比较，如果比最大值大，就不用再和最小值比较（或者先和最小值比较，如果比最小值小，就不用再和最大值比较），一般情况下，这种优化后的比较次数一定会少于2n

方法二：将数组元素按两个，两个分组，组内两元素有序存放，之后最小值跟组内较小的值比较，最大值只需跟组内较大的值比较，这样每组的比较次数是3，共n/2组，总的时间复杂度是3n/2次。

解：把数组两两一对分组，如果数组元素个数为奇数，就最后单独分一个，然后分别对每一组的两个数比较，把小的放在左边，大的放在右边，这样遍历下来，总共比较的次数是 N/2 次；在前面分组的基础上，那么可以得到结论，最小值一定在每一组的左边部分找，最大值一定在数组的右边部分找，最大值和最小值的查找分别需要比较N/2 次和N/2 次；这样就可以找到最大值和最小值了，比较的次数为

　　　　　　N/2 * 3 = (3N)/2 次

如图会更加清晰：

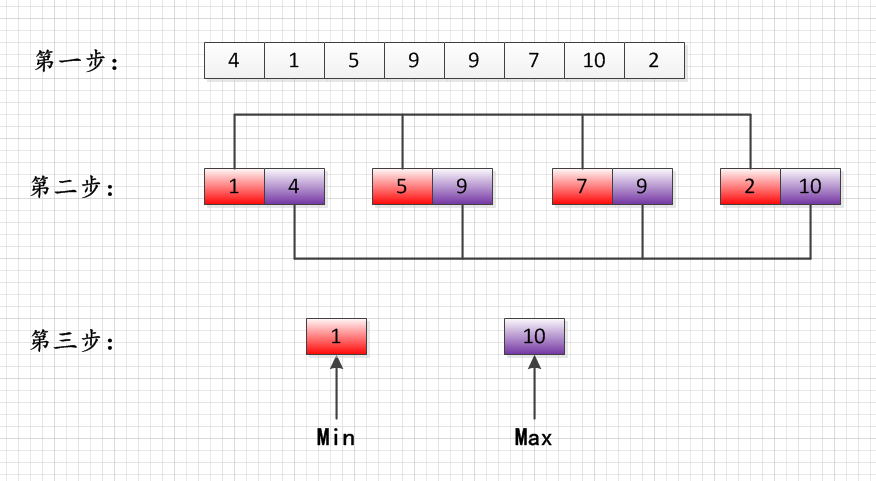
详情请参考http://blog.csdn.net/thebestdavid/article/details/11975809的第3题

#include <stdio.h>
#include <stdlib.h>
#define N 7
int main()
{
    int arr[N] = {4, 1, 5, 9, 9, 7, 10};
    int iter = 0;
    int cnt = 0;
    for(iter = 0; iter < N  ; iter += 2)
    {
        if(++cnt && arr[iter] > arr[iter + 1] )
        {
            int temp = arr[iter];
            arr[iter] = arr[iter + 1];
            arr[iter + 1] = temp;
        }
    }
    int myMin = arr[0];
    for(iter = 2; iter < N ; iter += 2)
    {
        if(++cnt && arr[iter] < myMin)
        {
            myMin = arr[iter];
        }
    }
    int myMax = arr[1];
    for(iter = 3; iter < N; iter += 2)
    {
        if(++cnt && arr[iter] > myMax)
        {
            myMax = arr[iter];
        }
    }
    if(N % 2 != 0 && ++cnt && myMax < arr[N - 1]) myMax = arr[N - 1];
    printf("min is %d\n", myMin);
    printf("max is %d\n", myMax);
    printf("compare times is %d", cnt);
    return 0;
}

分析：详情请参考http://blog.csdn.net/thebestdavid/article/details/11975809的第4题

解：这道题目有两个关键点：

　　第一个关键点： max{|x1-x2|,|y1-y2|} =（|x1+y1-x2-y2|+|x1-y1-(x2-y2)|）/2 --公式（1）

　　我们假设x₁=a[ i ]，x₂=b[ j ]，x₃=c[ k ]，则

Distance = max(|x₁ – x₂|, |x₁ – x₃|, |x₂ – x₃|) = max( max(|x₁ – x₂|, |x₁ – x₃|) , |x₂ – x₃|) --公式（2）

　　根据公式（1），max(|x₁ – x₂|, |x₁ – x₃|) = 1/2 ( |2x₁ – x₂– x₃| + |x₂ – x₃|)，带入公式（2），得到

Distance = max( 1/2 ( |2x₁ – x₂– x₃| + |x₂ – x₃|) , |x₂ – x₃| )

　　　　　　=1/2 * max( |2x₁ – x₂– x₃| , |x₂ – x₃| ) + 1/2*|x₂ – x₃| //把相同部分1/2*|x₂ – x₃|分离出来

　　　　　　=1/2 * max( |2x₁ – (x₂ + x₃)| , |x₂ – x₃| ) + 1/2*|x₂ – x₃| //把(x₂ + x₃)看成一个整体，使用公式（1）

　　　　　　=1/2 * 1/2 *((|2x₁ – 2x₂| + |2x₁ – 2x₃|) + 1/2*|x₂ – x₃|

　　　　　　=1/2 *|x₁ – x₂| + 1/2 * |x₁ – x₃| + 1/2*|x₂ – x₃|

　　　　　　=1/2 *(|x₁ – x₂| + |x₁ – x₃| + |x₂ – x₃|) //求出来了等价公式，完毕！

　　第二个关键点：如何找到(|x₁ – x₂| + |x₁ – x₃| + |x₂ – x₃|) 的最小值，x₁，x₂，x₃，分别是三个数组中的任意一个数，这一题，我只是做到了上面的推导，后面的算法设计是由csdn上的两个朋友想出来的方法，他们的CSDN的ID分别为 “云梦泽” 和 “ shuyechengying”.

算法思想是：

　　用三个指针分别指向a,b,c中最小的数，计算一次他们最大距离的Distance ，然后在移动三个数中较小的数组指针，再计算一次，每次移动一个，直到其中一个数组结束为止，最慢(l+ m + n)次，复杂度为O(l+ m + n)

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define l 3
#define m 4
#define n 6
int Mymin(int a, int b, int c)
{
    int Min = a < b ? a : b;
    Min = Min < c ? Min : c;
    return Min;
}

int Solvingviolence(int a[], int b[], int c[])
{
    //暴力解法，大家都会，不用过多介绍了！
    int i = 0, j = 0, k = 0;
    int MinSum = (abs(a[i] - b[j]) + abs(a[i] - c[k]) + abs(b[j] - c[k])) / 2;
//    int store[3] = {0};
    int Sum = 0;
    for(i = 0; i < l; i++)
    {
        for(j = 0; j < m; j++)
        {
            for(k = 0; k < n; k++)
            {
                Sum = (abs(a[i] - b[j]) + abs(a[i] - c[k]) + abs(b[j] - c[k])) / 2;
                if(MinSum > Sum)
                {
                    MinSum = Sum;
//                    store[0] = i;
//                    store[1] = j;
//                    store[2] = k;
                }
            }
        }
    }
//    printf("the min is %d\n", minABC);
//    printf("the three number is %-3d%-3d%-3d\n", a[store[0]], b[store[1]], c[store[2]]);
    return MinSum;

}

int MinDistance(int a[], int b[], int c[])
{
    int MinSum = 0; //最小的绝对值和
    int Sum = 0;  //计算三个绝对值的和，与最小值做比较
    int MinOFabc = 0; // a[i] , b[j] ,c[k]的最小值
    int cnt = 0;  //循环次数统计，最多是l + m + n次
    int i = 0, j = 0, k = 0;  //a,b,c三个数组的下标索引
    MinSum = (abs(a[i] - b[j]) + abs(a[i] - c[k]) + abs(b[j] - c[k])) / 2;
    for(cnt = 0; cnt <= l + m + n; cnt++)
    {
        Sum = (abs(a[i] - b[j]) + abs(a[i] - c[k]) + abs(b[j] - c[k])) / 2;
        MinSum = MinSum < Sum ? MinSum : Sum;
        MinOFabc = Mymin(a[i] ,b[j] ,c[k]);//找到a[i] ,b[j] ,c[k]的最小值
        //判断哪个是最小值，做相应的索引移动
        if(MinOFabc == a[i])
        {
            if(++i >= l) break;
        }//a[i]最小,移动i

        if(MinOFabc == b[j])
        {
            if(++j >= m) break;
        }//b[j]最小,移动j
        if(MinOFabc == c[k])
        {
            if(++k >= n) break;
        }//c[k]最小,移动k

    }
    return MinSum;
}
int main(void)
{
    int a[l] = {5, 6, 7};
    int b[m] = {13, 14, 15, 17};
    int c[n] = {19, 22, 24, 29, 32, 42};

    printf("\nBy violent solution ,the min is %d\n", Solvingviolence(a, b, c));
    printf("\nBy Optimal solution ,the min is %d\n", MinDistance(a, b, c));
    return 0;
}

29（8分）在黑板上写下50个数字：1至50。在接下来的49轮操作中，每次做如下动作：选取两个黑板上的数字a和b檫去，在黑板上写|b-a|。请问最后一次动作之后剩下数字可能是什么？为什么？（不用写代码，不写原因不得分）

分析：50以内的奇数都有可能，详情请参考http://blog.csdn.net/thebestdavid/article/details/11975809的评论

答案来自评论：

首先证明不可能是偶数：

设黑板上数字的总和是s，那么题目要求就是经过49次擦除之后，这个s的可能值。

假设在某一次擦除的数字为x1和x2，则有s=s-x1-x2+abs（x1-x2），也就是如果x1>x2,那么s=s-2*x2，如果x2>x1,那么s=s-2*x1。说明每一次擦除都是s减去一个偶数

再因为一开始s=1至50的和，是一个奇数，一个奇数减去49个偶数，结果一定不可能是一个偶数。在这里我们把所有的偶数都排除掉了。

那么接下来证明，1至49任意奇数是可能的。

首先结果是奇数的情况如下：
（1）（2,3）（4,5）。。。（48,49）（50）-->49
(1,2), (3), (4,5) ... (48,49), (50)--47
。
。
。
(1,2)....(47,48),(49)(50)-->1
所以说可能的结果是1到49所有的奇数啦，
（相邻的两个数差是1, 24个1可以得到结果0喽，然后用50减去留下的那个奇数，就得到与它对应的一个奇数哦，是不是这么想比较简单呢）！

【算法工程师附加题】请设计一个算法，在满足质因数仅为3,5,7或其组合的数中，找出第K大的数。比如K=1,2,3时，分别应返回3,5,7。要求算法时间复杂度最优。

分析：满足质因数仅为3,5,7或其组合的数，貌似可以表示成a(n)=3ⁱ*5^j*7^k，然后用基数排序，貌似方法不好使……

--------未完，待补充

posted on 2014-03-07 11:14 theCambrian.cpp 阅读(731) 评论(0) 编辑收藏举报

刷新页面返回顶部

Cambrian.cpp

阿里巴巴集团2014校园招聘笔试题（研发工程师--北邮站）

导航

公告