BZOJ 1047 理想的正方形

       看到这到题，第一反应当然是暴搜一遍，但是数据较大，暴搜铁定过不了，自然想到进行优化，优化的方案很多，每个人的思路可能不同，在这里我的思路仅供参考。

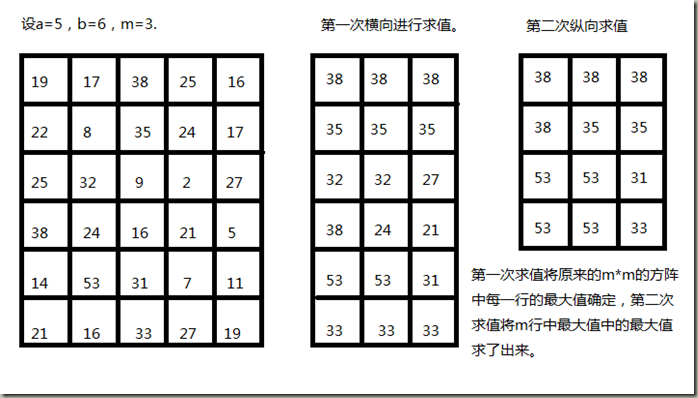
        我的想法是用单调队列、单调栈，当然简单的单调队列、单调栈只适用于一行数据，对于这道题要进行一定的组合和变换。根据题目的介绍，可以大致总结出以下信息：第一，矩阵由b组长度为a的数列组成；第二，求的范围是m*m。因而，我们可以先取第一行进行考虑，简单的理解为依次输入每一个数据，输入一个求取一下后m个数据中的最大值，并将之记录进一个新建数组，求取过程就是最裸的单调队列、单调栈，将每一行进行求值得到了一组新数据，这组数据记录了原数据横向上每m个中的最大值，也就是m*m方阵中每行的最大值，再将数据按竖着的方向进行上述操作，输入一个求一次后m个中的最大值，这样得到的就是最终结果。（如果有不理解的，请看下图）

题目的大致程序如下：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#define inf 0x3f3f3f3f

using namespace std;

int i_long,i_wide,i_side;
int g[1005][1005],f[1005][1005][2],t[1005][1005];
struct qu
{
    int i_value,p;
}q[1005];

void Getgf(int k)
{
    for (int j=1;j<=i_wide;j++)
    {
        int l=1,r=0;
        for (int i=1;i<=i_long;i++)
        {
            while (r&&r>=l&&t[i][j]<=q[r].i_value) r--;
            while (l&&l<=r&&q[l].p<=i-i_side) l++;
            
            q[++r].i_value=t[i][j];
            q[r].p=i;
            g[i][j]=q[l].i_value;
        }
    }
    for (int i=i_side;i<=i_long;i++)
    {
        int l=1,r=0;
        for (int j=1;j<=i_wide;j++)
        {
            while (r&&r>=l&&g[i][j]<=q[r].i_value) r--;
            while (l&&l<=r&&q[l].p<=j-i_side) l++;
            
            q[++r].i_value=g[i][j];
            q[r].p=j;
            f[i][j][k]=q[l].i_value;
        }
    }
}

int main()
{
    scanf("%d%d%d",&i_long,&i_wide,&i_side);
    for (int i=1;i<=i_long;i++)
    {
        for (int j=1;j<=i_wide;j++)
        {
            scanf("%d",&t[i][j]);
         }    
    }
        
    Getgf(0);
    
    for (int i=1;i<=i_long;i++)
    {
        for (int j=1;j<=i_wide;j++)
        {
            t[i][j]=-t[i][j];
        }         
    }
        
    Getgf(1);
    
    int ans=inf;
    for (int i=i_side;i<=i_long;i++)
    {
        for (int j=i_side;j<=i_wide;j++)
        {
            ans=min(ans,-f[i][j][1]-f[i][j][0]);
        }  
    }
        
    cout<<ans<<endl;
    
    return 0;
}

希望所写内容对您有所帮助，谢谢。