LightOJ 1214 Large Division

Large Division

　　Given two integers, a and b, you should check whether a is divisible by b or not. We know that an integer a is divisible by an integer b if and only if there exists an integer c such that a = b * c.

Input

　　Input starts with an integer T (≤ 525), denoting the number of test cases.

　　Each case starts with a line containing two integers a (-10²⁰⁰ ≤ a ≤ 10²⁰⁰) and b (|b| > 0, b fits into a 32 bit signed integer). Numbers will not contain leading zeroes.

Output

　　For each case, print the case number first. Then print 'divisible' if a is divisible by b. Otherwise print 'not divisible'.

Sample Input

6

101 101

0 67

-101 101

7678123668327637674887634 101

11010000000000000000 256

-202202202202000202202202 -101

Sample Output

Case 1: divisible

Case 2: divisible

Case 3: divisible

Case 4: not divisible

Case 5: divisible

Case 6: divisible

 

解题思路：
　　本题考查大数运算，每次测试给定一个整数T为测试数量，之后跟随T行，每行都给出两个数字，第一个数字是一个大于10²⁰⁰  且小于10²⁰⁰的数字，第二个数字是一个32位的int，要求计算第一个数是否可以整除第二个数，若可以整除输出divisible否则输出not divisible。

　　由于第一个数字超出可以直接存储的范围太多，我们不能直接对其进行运算，那么就换一种运算方式，按位对其进行运算，至于如何按位运算，小学时学过对数字运算极为方便的方法——竖式。

　　以12345678 / 9为例子

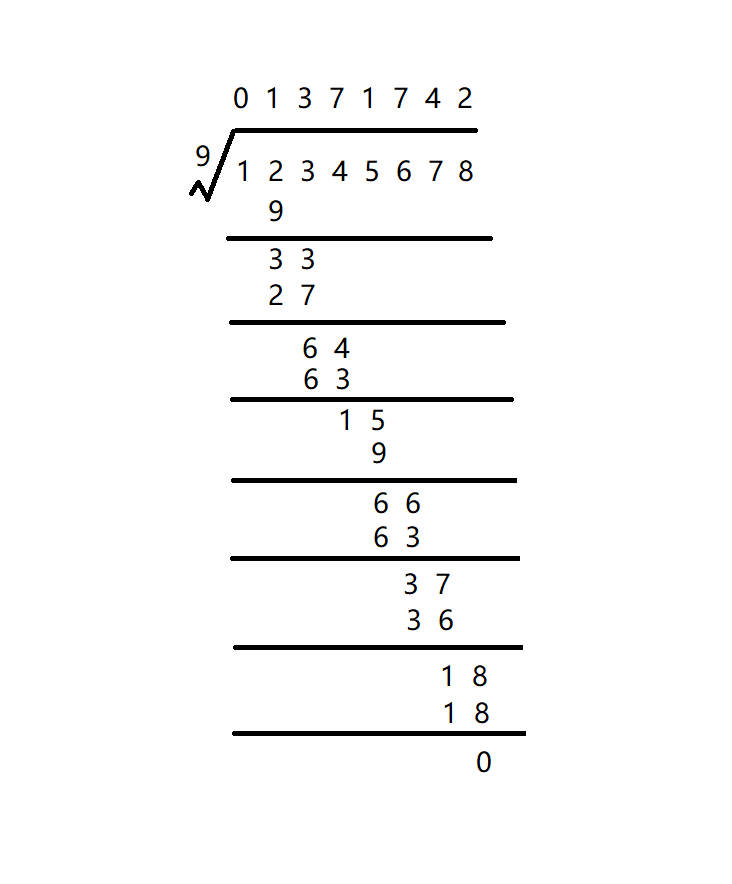
　　由于题目中已经告诉我们输入的数字中不包含先导0，所以按照小学的算法我们用第一个数首位除数除以第二个数，9 除以 1得0余1，继续运算将余数1与下一个数结合得到12， 12除以9得1余3，将3与下一个数结合，得到33，以此类推直到运算到最后一位，我们便可以得到最终的余数。之后判断余数是否为0就可以得出答案。

 

　　

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 200+10;
struct Big{ //Big储存输入的大数
    int num[maxn];
    int len;
    Big(){
        len = 0;
        memset(num, 0, sizeof(num));
    }
};
int divide(Big a, int b){   //传入被除数与除数
    Big c;
    LL mod = 0; //mod记路余数
    for(int i = 0; i < a.len; i++){ //从首位开始按位运算
        mod = mod * 10 + a.num[i];  //mod要用long long 因为mod * 10后可能超int范围
        if(mod >= b)    //如果除不开就去计算下一位，除的开就进行计算
            mod = mod % b;  //当前值除以b找到新的余数
    }
   return (int)mod;
}
int main()
{
    int t, b;   //t为测试数量
    string str; //str记录输入第一个数字
    while(scanf("%d", &t) != EOF){
        for(int i = 1; i <= t; i++){
            cin >> str >> b;
            Big a;  //a记录第一个数
            if(str[0] == '-'){  //第一个数字如果是负数就去掉符号
                int cnt = 0;
                a.len = str.size() - 1;
                for(string::iterator it = ++str.begin(); it != str.end(); it++){
                    a.num[cnt++] = *it - '0';
                }
            }else{  //正数直接记录入a
                int cnt = 0;
                a.len = str.size();
                for(string::iterator it = str.begin(); it != str.end(); it++){
                    a.num[cnt++] = *it - '0';
                }
            }
            if(b < 0)
                b = -b;
            if(!divide(a, b)){  //只要mod为0就可以整除，否则不能整除
                printf("Case %d: divisible\n", i);
            }else{
                printf("Case %d: not divisible\n", i);
            }
        }
    }
    return 0;
}