20162330 2017-2018-1《程序设计与数据结构》第十周学习总结

2017-2018-1 学习总结目录：　1　2　3　5　6　7　9　10　11　12


目录


教材学习内容总结

第19章 图

无向图

  • 图的概念（非线性结构）：允许树中每个结点与多个结点相连，不分父子结点。

  • 图由 顶点 和 边 组成。

顶点由名字或标号来表示，如：A、B、C、D；
边由连接的定点对来表示，如：（A,B）,（C,D），表示两顶点之间有一条边。

  • 无向图：顶点之间无序连接。
    如：边（A,B）意味着A与B之间的连接是双向的，与（B,A）的含义一样。

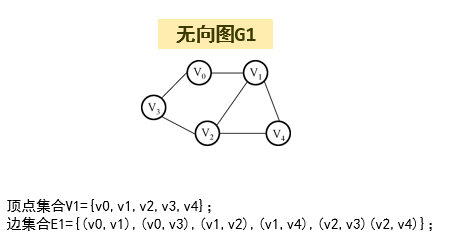
  • 邻接（邻居）：两个顶点之间有边连接。

  • 自循环（悬挂）：自己连接到自己的边。

  • 完全图：含有最多条边的无向图。例如：

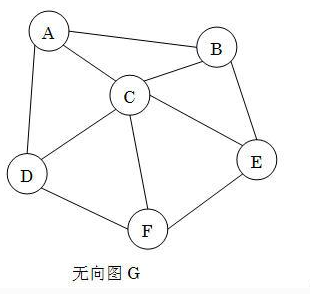
无向图G是一个完全图。

  • 路径：连接图中两个顶点的边的序列，可以由多条边组成。

无向图中的路径是双向的。

  • 路径长度：路径中所含边的数目（顶点个数减1）。

  • 联通图：无向图中任意两个顶点间都有路径。例如：

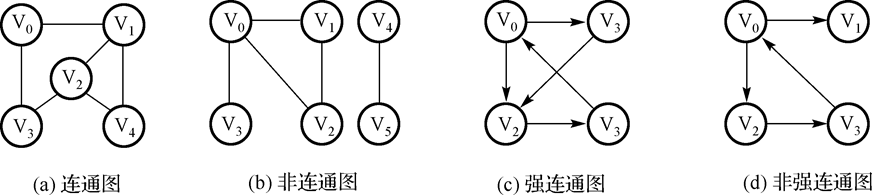
完全图一定是连通图，连通图不一定是完全图。

  • 环（回路）：第一个顶点与最后一个顶点相同且没有重复边的路径。例如：

  • 无环图：没有环的图。

  • 子图：类似集合中“子集”的概念，示例如下：

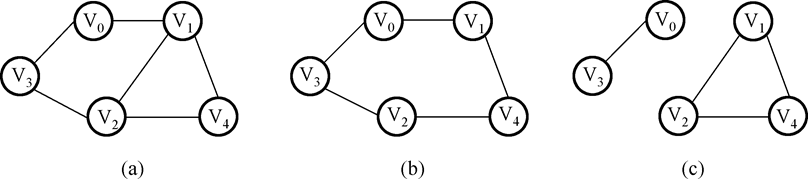
    其中，（b），（c）是（a）的子图。

  • 生成树：包含无向图G1所有顶点的极小连通子图称为G1的生成树。例如：

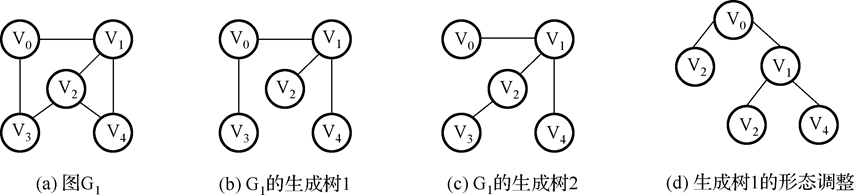
  • 稀疏图与稠密图：有很少条边或弧（如 e < n log\(_n\)，n 是图的顶点数，e 是弧数）的图称为稀疏图，反之称为稠密图。

有向图

  • 有向图：顶点之间有序连接，边是顶点的有序对。

边（A,B）和（B,A）方向不同。

  • 有向路径：连接两个顶点有向边的序列。

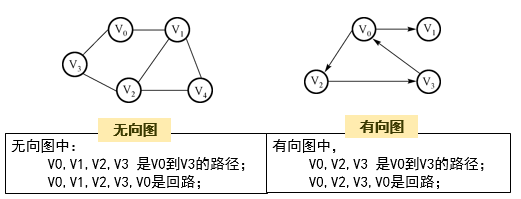
  • 有向图中的有序对常用序偶表示，例如：

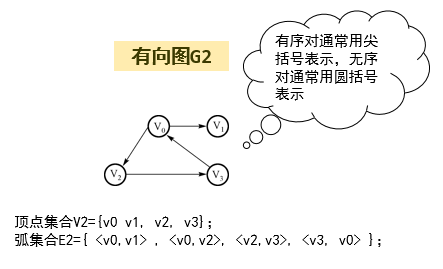
    上图中路径 V\(_0\)→V\(_2\)→V\(_3\) 是从V\(_0\)到V\(_3\)的路径，但是反过来不再成立。

  • 注意联通有向图与无向图不同，有向边决定连通性。例如：

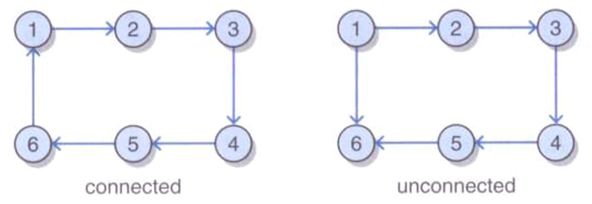
上图中左图为联通图，右图不联通，因为从任何顶点到顶点1都没有路径。

  • 有向树是一个有向图，其中指定一个元素为根，则具有下列特性：

    任何顶点到根都没有连接。

    到达每个非根元素的连接都只有一个。

    从根到每个顶点都有路径。

  • 顶点的度、出度、入度：

带权图

  • 带权图（网络）：每条边都对应一个权值（数据信息）的图。（城市之间的航线、票价等）

带权图可以是无向的也可以是有向的。

  • 带权图的边：由起始点、结束点和权构成。

有向图的每条边必须使用三元组表示。

常用的图算法

  • 图的遍历：

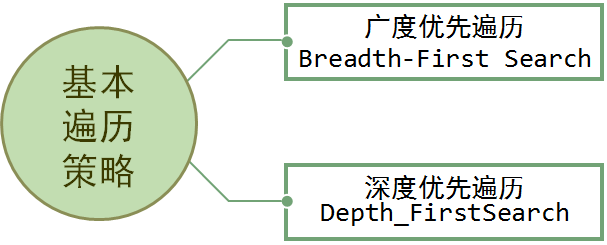
  • 广度优先遍历：从一个顶点开始，辐射状地优先遍历其周围较广的区域。

  • 深度优先遍历：图的深度优先搜索，类似于树的先序遍历，所遵循的搜索策略是尽可能“深”地搜索图。

  • 连通性：从任意结点开始的广度优先遍历中得到的顶点数等于图中所含顶点数。

  • 生成树：包含图中所有顶点及图中部分边的一棵树。
    最小生成树：所含边权值之和小于其他生成树的边的权值之和。

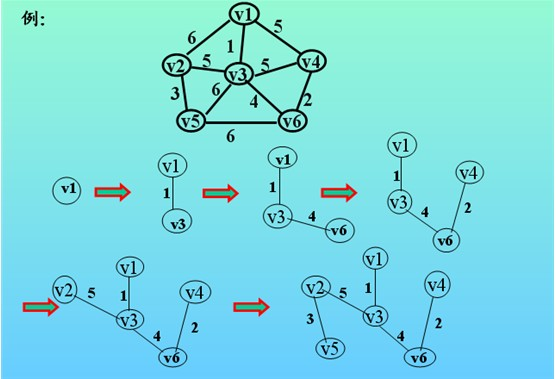
  • 判定最短路径：

① 判定起始顶点和目标顶点之间是否存在最短路径（两个顶点之间边数最少的路径）。
② 在带权图中找到最短路径。（Dijkstra算法）

图的实现策略：

  • 邻接矩阵：

  • 无向图邻接矩阵：

特点：对称，可压缩存储。顶点 vi 的度是邻接矩阵中第 i 行 1 的个数。

  • 有向图邻接矩阵：

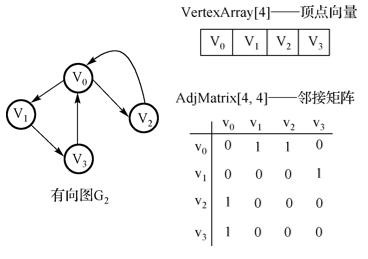
特点：不一定对称。顶点 vi 的出度是邻接矩阵中第 i 行 1 的个数。顶点 vi 的入度是邻接矩阵中第 i 列 1 的个数。

  • 网的邻接矩阵：

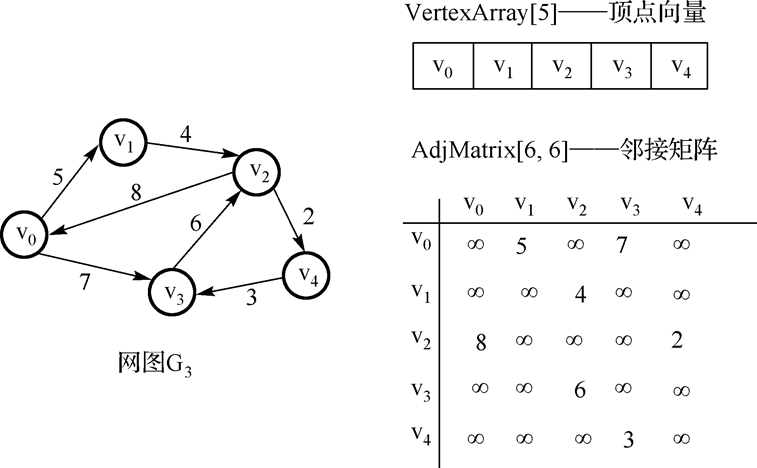
  • 采用邻接矩阵表示图，优点：直观方便，运算简单。

时间复杂度：边查找O（1）；顶点度计算O（n）。
空间复杂度：O（n\(^2\)）（尽量不要用来表示稀疏图）。

  • 边集数组：

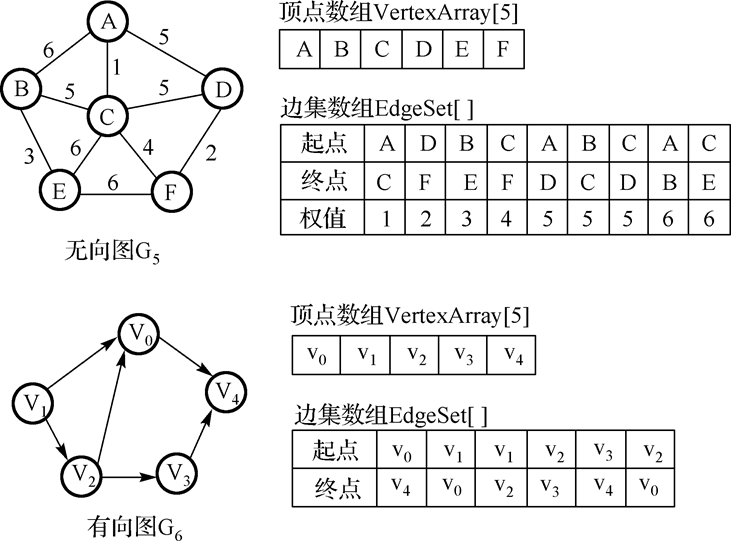
在边集数组中查找一条边或一个顶点的度都需要扫描整个数组，所以其时间复杂性为O（e）。
边集数组适合那些对边依次进行处理的运算，不适合对顶点的运算和对任一条边的运算。
边集数组表示通常包括一个 边集数组和一个顶点数组，所以其空间复杂性为O（n+e）。
从空间复杂性上讲， 边集数组也适合表示稀疏图。

  • 无向图邻接表：

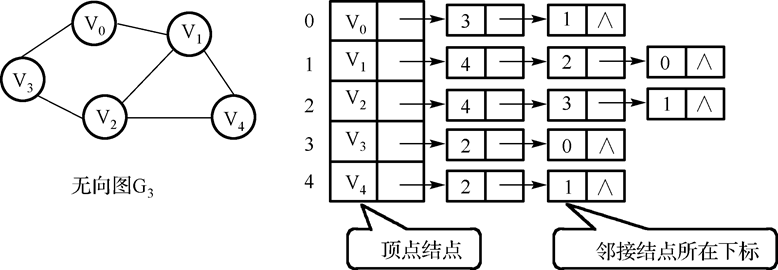
特点：若无向图中有 n 个顶点、e 条边，则其邻接表需 n 个头结点和 2e 个表结点。适宜存储稀疏图。
无向图中顶点 vi 的度为第 i 个单链表中的结点数。

  • 有向图邻接表：

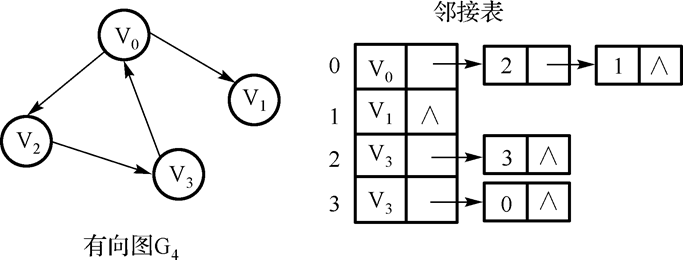
特点：顶点 vi 的出度为第 i 个单链表中的结点个数。
顶点 vi 的入度为整个单链表中邻接点域值是 i -1 的结点个数。
找出度易，找入度难。

  • 逆邻接表：

特点：顶点 vi 的入度为第 i 个单链表中的结点个数。
顶点 vi 的出度为整个单链表中邻接点域值是 i -1 的结点个数。
找入度易，找出度难。

  • 带权邻接表：

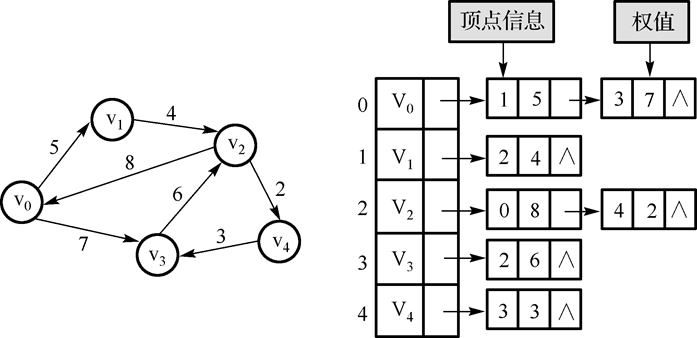
  • 邻接表用于表示稀疏图比较节省存储空间，因为只需要很少的边结点，若用于表示稠密图，则将占用较多的存储空间，同时也将增加顶点的查找结点时间。

  • 十字链表：

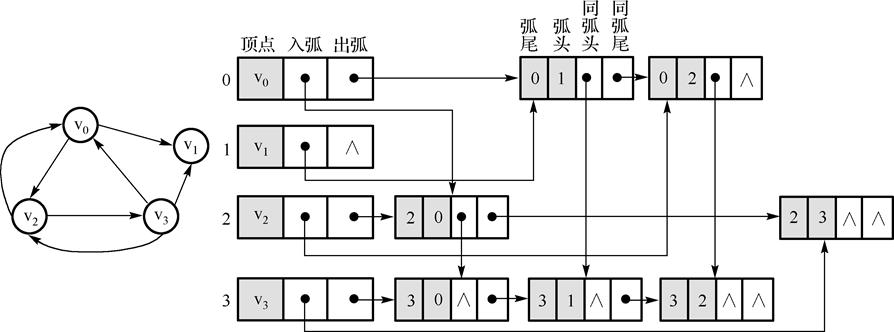
十字链表除了结构复杂一点外，其创建图的时间复杂度是和邻接表相同的，用十字链表来存储稀疏有向图，可以达到高效存取的效果。

  • 邻接多重表：

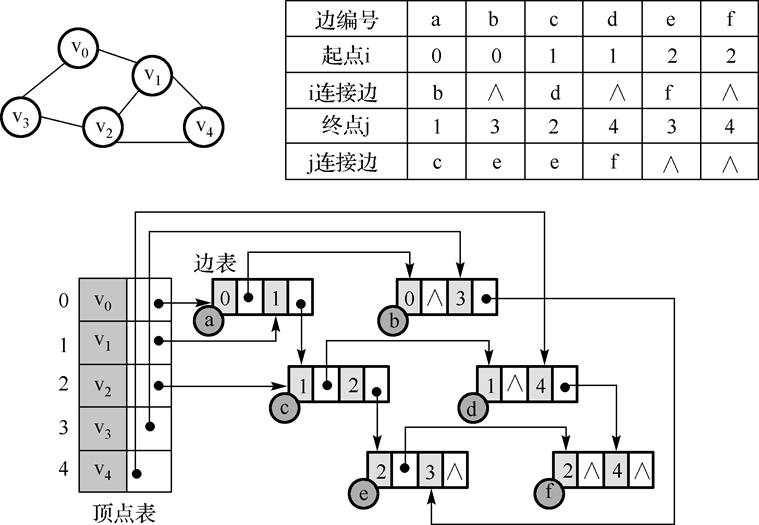
邻接多重表容易操作，如求顶点的度等。建立邻接多重表的空间复杂度与时间复杂度都与邻接表相同。

  • 图的存储结构归结比较：

【返回目录】


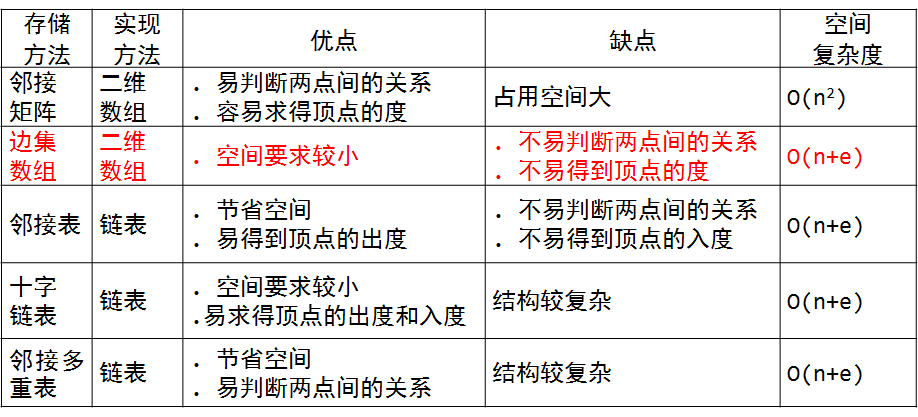
教材学习中的问题和解决过程

  • 【问题1】：为什么边集数组中所含元素的个数要大于等于图中边的条数？

  • 解决方案 ：（看PPT，查找相关资料）
    发现自己最初的理解有误，我最初的理解是对于整个图而言，例如下面的图：

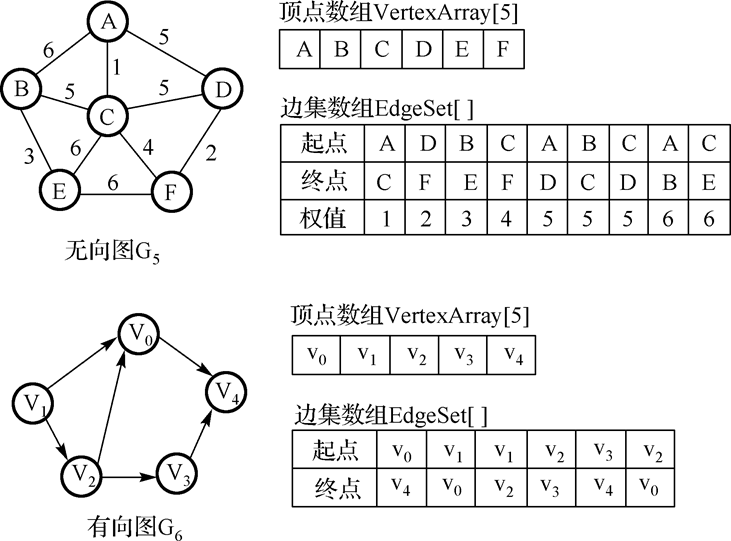
    无向图G5中的边的条数就大于元素个数，所以如果是规定的话，为什么还可以用边集数组表示？
    在依次查找了相关词条定义后发现限定词“该数组中”，又翻看之前的PPT，于是恍然大悟，原来是自己最初的理解范围错了。在该数组中，所含元素的个数必然是大于等于图中边的条数的：

【返回目录】


代码调试中的问题和解决过程

  • 正在学习代码中...

【返回目录】


代码托管

  • 本周代码上传至 test/ch13 和 cn.edu.besti.cs1623.LWK2330 两个文件夹里：
    （statistics.sh脚本的运行结果截图）

上周考试错题总结

  • 【错题1】If a binary search tree becomes unbalanced after an element is added, it is sometimes possible to efficiently rebalance the tree by ___________________ .
    A.using left and right rotations
    B.selecting a leaf node to use as a new root
    C.reconstructing the tree from scratch
    D.all of the above
    E.it is impossible to rebalance a tree efficiently

  • 错误原因：理解错误，错选D。
    解析：左旋转和右旋转可以帮助树恢复平衡。

  • 【错题2】Finding an element in a binary search tree always requires O(log\(_2\)n) comparisons.
    A.true
    B .false

  • 错误原因：考虑情况不全面，错选A。
    加深理解：如果 n 是一个退化的二叉搜索树，在最坏的情况下，找到一个元素可能需要复杂度为 O(n) 的比较。

  • 【错题3】Whenever a new element is added to a maxheap, it always becomes the root.
    A.true
    B .false

  • 错误原因：理解错误，理解为获取最大元素，所以错选A。
    解析：添加到 maxheap 的新元素可能会也可能不会成为根。

  • 【错题4】A heap sort sorts elements by constructing a heap out of them, and then removing them one at a time from the root.
    A.true
    B .false

  • 错误原因：我看了解析，觉得选A没错。
    解析：堆排序使用堆属性来对元素进行排序，通过构造一个堆，然后逐个删除它们。

【返回目录】


结对及互评

本周结对学习情况

  • 莫礼钟本周有点浪，和我一起学习的内容零零碎碎，不过好事是他本周的听课效率比较高，还特意为我讲解了十字链表表示图的画法。但是我还发现，一些常用的内容，比如：数组元素个数和索引的关系，莫礼钟还是有些分不清，希望一定重视基础内容。

  • 20162319

    • 结对学习内容
      • 十字链表表示图
      • SequenceSearch算法实现
      • 数组异常及基本内容

其他（感悟、思考等，可选）

　　本周我没有将大部分精力用在这门课程上，可以说是“短暂地休息了一下”，再加上图的概念内容比较多，所以理论方面和代码方面的内容都没有全面地学习完，下周当然还要花时间弥补回来。最近真的有点缺少行动力，又时不时感到一些焦虑，真的感到学习质量有些下降。
　　另外这几周的博客质量也下降了不少。对于博客，我还是看重质而不看重量的，在这个问题上我觉得自己是清醒的，一篇博客不论写得有多差，自己都应该反复读读，没有补全的内容后期一定记得补全。博客园我平均一天登录几次，每次在浏览自己上学期的博客时，总觉得这学期博客的质量下降了，可能是因为自己最近有些懈怠，也可能有些形式主义。对自己的要求要适度，避免行动过于拖延。总之，最后的这几周，一定要挺过去。

  • 【附】教材及考试题中涉及到的英语：
    Chinese English Chinese English
    顶点 vertice 邻接的 adjacent
    自循环 self-loop 悬挂 sling
    无环图 acyclic 无向图 undirected graph
    有向图 digraph 有向图 directed graph
    带权图 weighted graph 深度优先遍历 depth-first traversal
    广度优先遍历 breadth-first traversal 生成树 spanning tree
    邻接矩阵 adjacency matrix 列 column

【返回目录】


学习进度条

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积） 重要成长
目标 5000行 30篇 400小时
第一周 234/234 1/28 14/14 了解算法效率、大O符号等理论内容
第二周 255/489 1/29 12/26 了解敏捷的团队、泛型的使用
第三周 436/925 2/31 10/36 了解一些查找和排序的算法
第四周 977/1902 3/34 10/46 掌握实现线性结构
第五周 800/2702 2/36 12/58 掌握实现栈集合
第六周 260/2962 1/37 8/64 掌握实现队列集合
第七周 843/3805 4/41 12/76 掌握实现树的基本结构
第八周 738/4543 1/42 12/88 二叉树实验（查找树、平衡树）
第九周 1488/6031 2/44 15/103 掌握堆的实现、哈夫曼树基本结构
第十周 1340/7371 2/46 12/115 查找与排序实验、图的基本概念及实现方法

  • 计划学习时间：20小时

  • 实际学习时间：12小时

  • 有效学习时间：4小时

  • 改进情况：本周有些懈怠，投入本课程的学习时间太少，不论是理论知识的理解还是代码实现都不够深刻，属于个人原因，下周必须投入更多时间弥补一下。


参考资料

【返回目录】

posted @ 2017-11-12 23:35  N-Liu  阅读(325)  评论(1)  编辑  收藏  举报