20162330 2017-2018-1《程序设计与数据结构》第九周学习总结

2017-2018-1 学习总结目录：　1　2　3　5　6　7　9　10　11　12


目录


教材学习内容总结

第18章 队和优先队列

堆

  • 堆是一棵完全二叉树。（平衡、约束）

  • 分类：最大堆（大顶堆）、最小堆（小顶堆）。

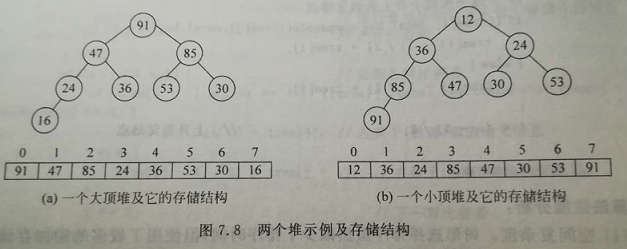
  • 基本操作：添加元素、找到最大值、删除最大值。

  • 添加元素：将元素添加为新的叶结点，同时保持树是完全树，将该元素向根的地方移动，将它与父结点对换，直到其中的元素大小关系满足要求为止。

  • 找到最大元素：此操作较简单，因为在添加元素的过程中就已经把最大元素移动到了根位置。

  • 删除最大元素：利用最后的叶结点来取代根，然后将其向下移动到合适的位置。

  • 堆和二叉排序树的区别：

1.堆是一棵完全二叉树，二叉排序树不一定是完全二叉树；
2.在二叉排序树中，某结点的右孩子结点的值一定大于该结点的左孩子结点的值，在堆中却不一定；
3.在二叉排序树中，最小值结点是最左下结点，最大值结点是最右下结点。在堆中却不一定。

堆的实现

  • 最大堆接口的实现：
public interface MaxHeap<T extends Comparable<T>> extends BinaryTree<T>
{
    //  Adds the specified object to the heap.
    public void add (T obj);

    //  Returns a reference to the element with the highest value in the heap.
    public T getMax ();

    //  Removes and returns the element with the highest value in the heap.
    public T removeMax ();
}

  • 在 LinkedMaxHeap 中的 add 方法依赖于HeapNode中的两个方法：getParentAdd 和 heapifyAdd 方法。

  • 其中 getParentAdd 方法从树的最后一个结点开始，一个一个检测，寻找新加入结点的父结点。从树中开始向上查找，直到发现它是某个结点的左子结点，或是到达根结点时为止。如果到达根结点，新的父结点是根的左后继结点。如果没有到达根结点，则再查找右子结点的最左后继。

    public HeapNode<T> getParentAdd (HeapNode<T> last)
{
    HeapNode<T> result = last;

    while ((result.parent != null) && (result.parent.left != result))
        result = result.parent;

    if (result.parent != null)
        if (result.parent.right == null)
            result = result.parent;
        else
        {
            result = (HeapNode<T>) result.parent.right;
            while (result.left != null)
                result = (HeapNode<T>) result.left;
        }
    else
        while (result.left != null)
            result = (HeapNode<T>) result.left;

    return result;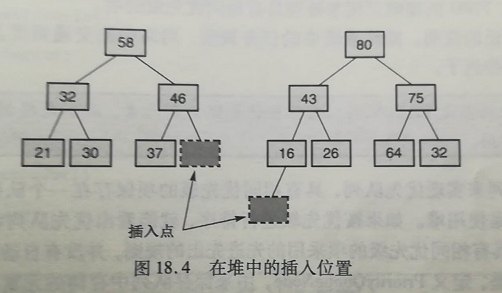
}

  • 一旦新的叶结点添加到树中，heapifyAdd 方法就利用 parent 引用沿树向上移动，必要时交换元素。（交换的是元素，不是结点）

    public void heapifyAdd (HeapNode<T> last)
{
    T temp;
    HeapNode<T> current = last;

    while ((current.parent != null) &&
            ((current.element).compareTo(current.parent.element) > 0))
    {
        temp = current.element;
        current.element = current.parent.element;
        current.parent.element = temp;
        current = current.parent;
    }
}

堆排序

  • 思路：将一组元素一项项地插入到堆中，然后一次删除一个。因为最大元素最先从堆中删除，所以一次次删除得到的元素将是有序序列，而且是降序的。同理，一个最小堆可用来得到升序的排序结果。

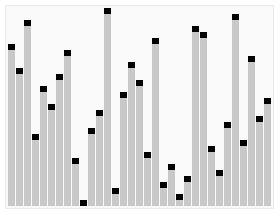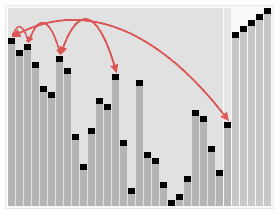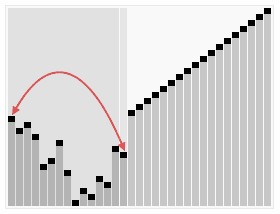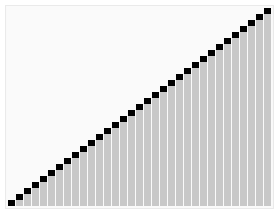
优先队列

  • 两个规则：

① 具有更高优先级的项排在前面。（不是FIFO）
② 具有相同优先级的项按先进先出的规则排列。（FIFO）

  • 实现方法：定义结点类保存队列中的元素、优先级和排列次序。然后，通过实现 Comparable 接口定义 compareTo 方法，先比较优先级，再比较排列次序。

【返回目录】


教材学习中的问题和解决过程

  • 【问题】：对于堆排序的详细步骤（具体顺序）不清楚，教材上也只提供了思路。

  • 解决方案 ：（查找相关资料）
    【步骤一】构造初始堆，以大顶堆为例，给无序序列构造一个大顶堆，假设无序序列如下：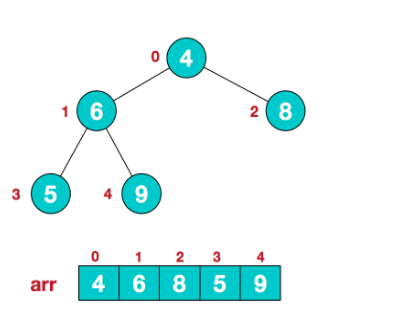

    从最后一个非叶子结点开始（叶结点不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整：

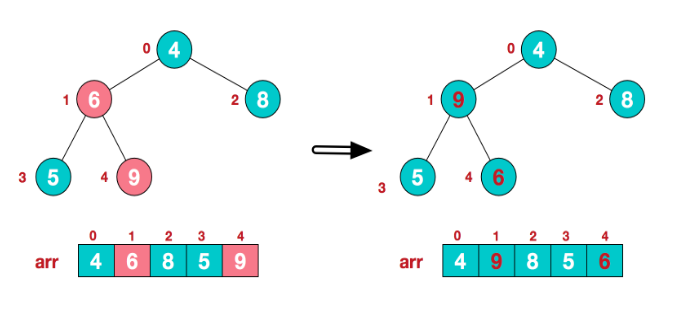
    找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。

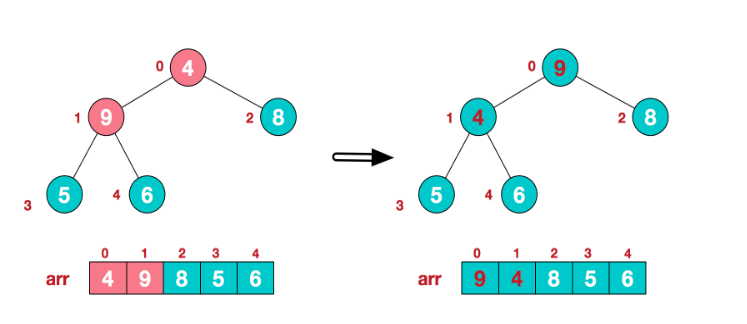
    这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

    这样大顶堆就完成了。

  • 【步骤二】将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。首先将堆顶元素9和末尾元素4进行交换：

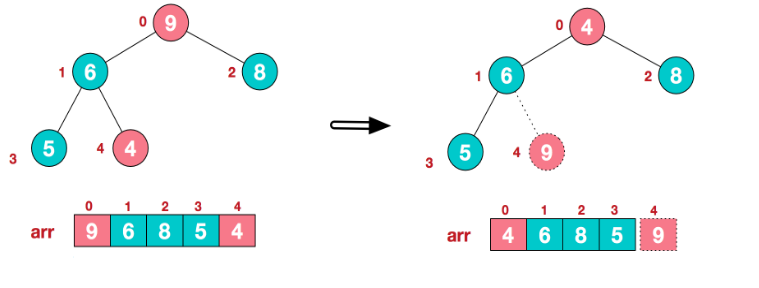
    重新调整结构，使其继续满足堆定义：

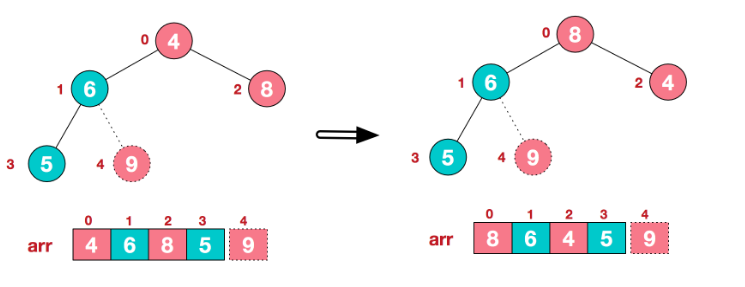
    再将堆顶元素8与末尾元素5进行交换，得到第二大元素8：

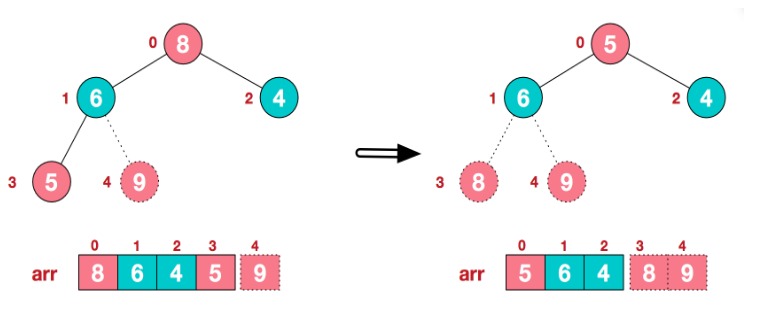
  • 【步骤三】如此反复进行交换、重建、交换。反复进行此过程，便可得到有序序列：

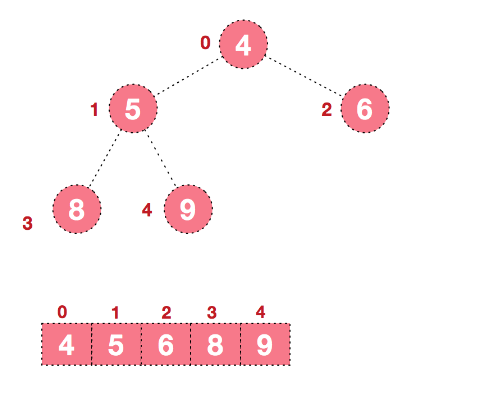
  • 所以，基本步骤概括为：将无序堆构建成大顶堆或小顶堆，再通过反复交换堆顶元素和当前末尾元素并调整，最后使整个序列有序。

【返回目录】


代码调试中的问题和解决过程

  • 【问题】：对于课本中出现的代码错误问题。

  • 解决方案：可以参考张之睿的解答：

【返回目录】


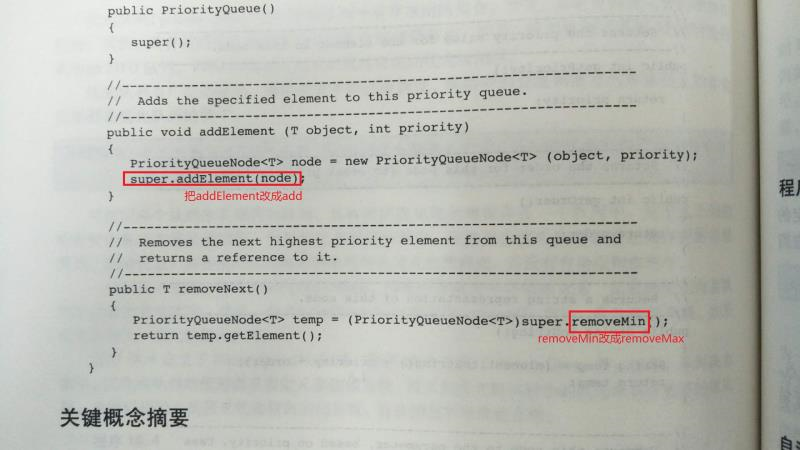
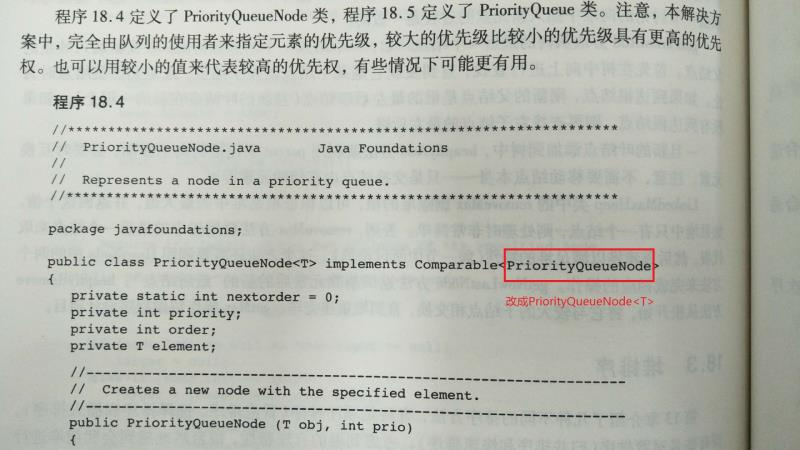
代码托管

  • 本周代码上传至 ch18 文件夹中：
    （statistics.sh脚本的运行结果截图）

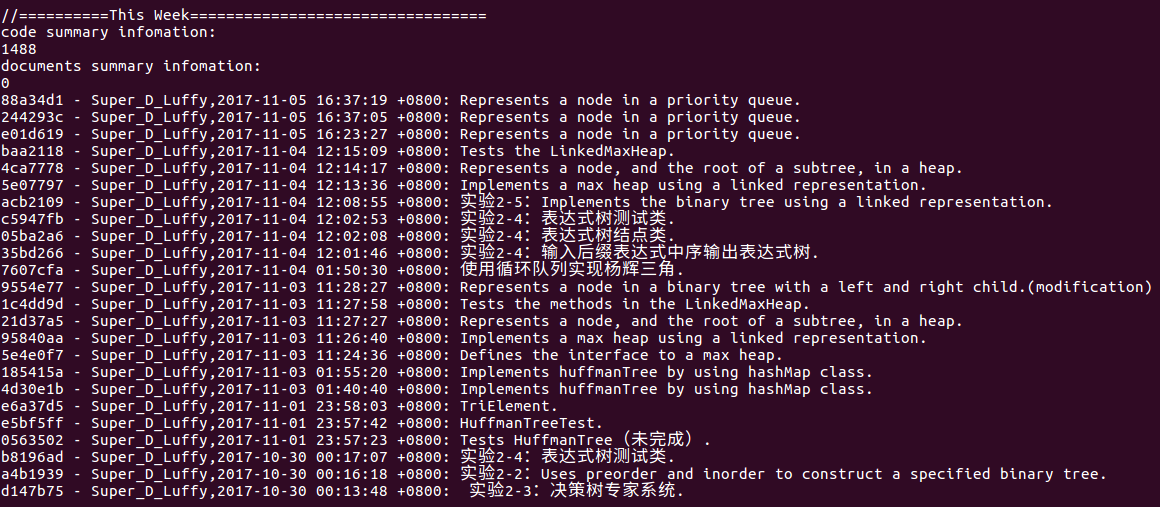
上周考试错题总结

  • 【错题1】Which of the following best describes a balanced tree?
    A .A balanced trees has all nodes at exactly the same level.
    B .A balanced tree has no nodes at exactly the same level.
    C .A balanced tree has half of the nodes at one level and half the nodes at another level.
    D .A balanced tree has all of the nodes within one level of each other.
    E .none of the above correctly describe a balanced tree.

  • 错误原因：做第一遍的时候我选了D，但是第二遍以为第一遍做错了，认为D只描述了平衡树的一种情况，不全面，所以错选E。
    加深理解：尽管树的所有结点都是完全相同的，但并不是所有的平衡树都具有这种特性。而D中的 within one level of each other 就相当于所有子结点彼此不超过一层。

  • 【错题2】In an inorder traversal, the elements of a tree are visited in order of their distance from the root.
    A .true
    B .false

  • 错误原因：这个题也是，第一遍我选了B，但是仔细一想感觉是错的，于是查了查 order 的意思，竟然查到了“分治”的意思，我一想中序遍历根结点在中间，就选了A。
    加深理解：层序遍历是根据元素与根之间的距离依次访问的。

【返回目录】


结对及互评

本周结对学习情况

  • 莫礼钟本周状态一般，不过主动承担了团队中的交互工作，负责与其他小组成员交流前几周的团队情况，完成得不错，还写了总结。对于其他内容的学习，有些断断续续，不够连贯，很多方面还需要补一下，刚好我也有一些需要补充的内容，打算下周再抽出一部分时间学习，毕竟我们的代码实践方面都比较弱，这次还要特别感谢莫礼钟以前的结对伙伴 杨京典 能够在晚上抽空来指导莫礼钟学习，主要是对于上次未完成实验的补充学习。

  • 20162319

    • 结对学习内容
      • 实验二 树
      • 哈夫曼树

其他（感悟、思考等，可选）

  • 本周可以说是忙绿而焦虑的一周，在经历了上周的实验之后，又恢复到教材内容学习的进程，本周的哈夫曼树我是硬生生地“啃”下来的，我再次感受到了数据结构的难度。可能是我的代码写得太少，很多算法都是只有思路而写不出代码，还有关于树的内容我需要及时梳理一下。关于团队项目，我们又经历了一次磨炼，我用了一个下午的时间学会了如何使 markdown 文件转换成 pdf 格式，并且又了解到几个新的 markdown 编辑器，还实验了一些码云上独特而恼人的 markdown 格式，大概本周我在这上面花费的时间多一些吧。

  • 【附1】教材及考试题中涉及到的英语：

    Chinese English Chinese English
    退化的 degenerate 后继承 successor
    属性 property 插图 illustration

  • 【附2】本周小组博客

【返回目录】


学习进度条

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积） 重要成长
目标 5000行 30篇 400小时
第一周 234/234 1/28 14/14 了解算法效率、大O符号等理论内容
第二周 255/489 1/29 12/26 了解敏捷的团队、泛型的使用
第三周 436/925 2/31 10/36 了解一些查找和排序的算法
第四周 977/1902 3/34 10/46 掌握实现线性结构
第五周 800/2702 2/36 12/58 掌握实现栈集合
第六周 260/2962 1/37 8/64 掌握实现队列集合
第七周 843/3805 4/41 12/76 掌握实现树的基本结构
第八周 738/4543 1/42 12/88 二叉树实验（查找树、平衡树）
第九周 1488/6031 2/44 15/103 掌握堆的实现、哈夫曼树基本结构

  • 计划学习时间：14小时

  • 实际学习时间：15小时

  • 有效学习时间：5小时

  • 改进情况：本周学习状态一般，比较稳定，团队项目耗时较多。另外，我的专注力不够，总是很容易被感兴趣的事分散，在个人学习上还需再加把劲！


参考资料

【返回目录】

posted @ 2017-11-05 23:39  N-Liu  阅读(259)  评论(1)  编辑  收藏  举报